Порядок побудови графіків

1. Тримаючи натиснутою клавішу Ctrl, відмічаємо лівою клавішею миші необхідні для побудови графіків блоки комірок із числовими даними: D35:D44; M35:M44; N35:N44. При переході до іншого блоку комірок ліву клавішу миші відпускаємо.

Діалогове вікно типів діаграм

2. На панелі інструментів наводимо курсор на значок Мастер диаграм і натискаємо ліву клавішу мишки. Відкривається перше діалогове вікно Мастер диаграм (шаг 1 из 4). У відкритому вікні вибираємо тип діаграм Точечная або График, також вибираємо його вид. Для переходу до наступного діалогового вікна натискуємо клавішу Далее>.

3. У діалоговому вікні Мастер диаграм (шаг 2 из 4) активізуємо позицію Подписи оси Х і відмічаємо курсором діапазон даних фактора Х (C35:C44). Натискаємо клавішу Далее>.

4. У діалоговому вікні Мастер диаграм (шаг 3 из 4) вводимо назви графіку і координати осей.

Натискаємо клавішу Далее>.

5. У діалоговому вікні Мастер диаграм (шаг 4 из 4) відмічаємо де помістити діаграму: на робочому аркуші, де проведені розрахунки; на окремому аркуші і клацаємо по книпці Готово.

Після натиснення клавіші Готово на робочому аркуші з’являється графік.

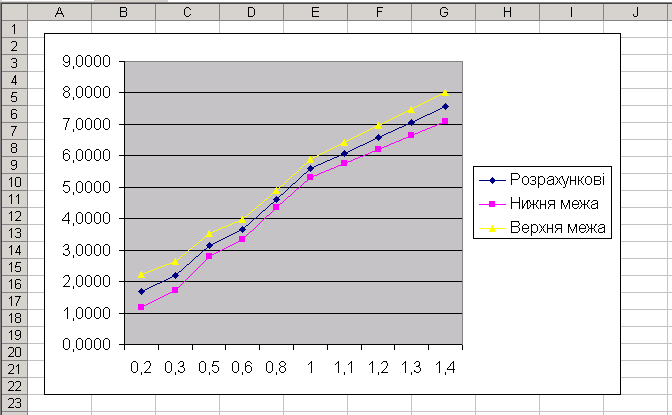
Для редагування графіка (або його частин) необхідно навести на нього курсор і натиснути 2 рази на ліву клавішу мишки.

7) Для перевірити виконання передумови 2 на рівні значущості за тестом Гейзера потрібно виконати наступні обчислення:

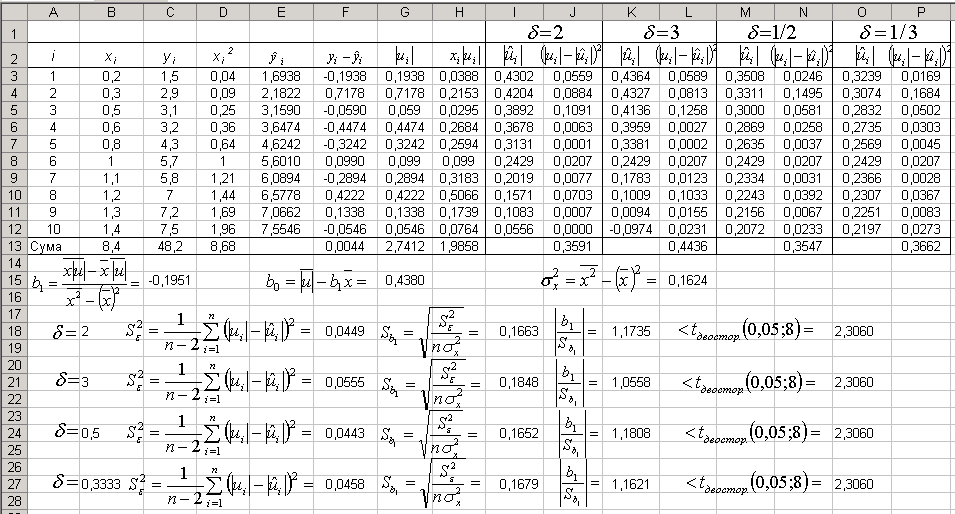
В режимі формул дана таблиця має вигляд:

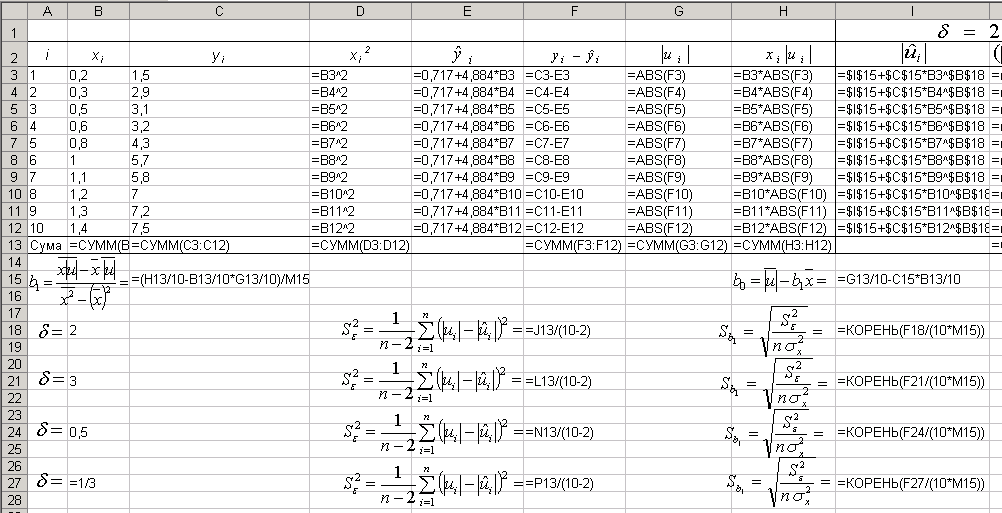
Продовження розрахункової таблиці:

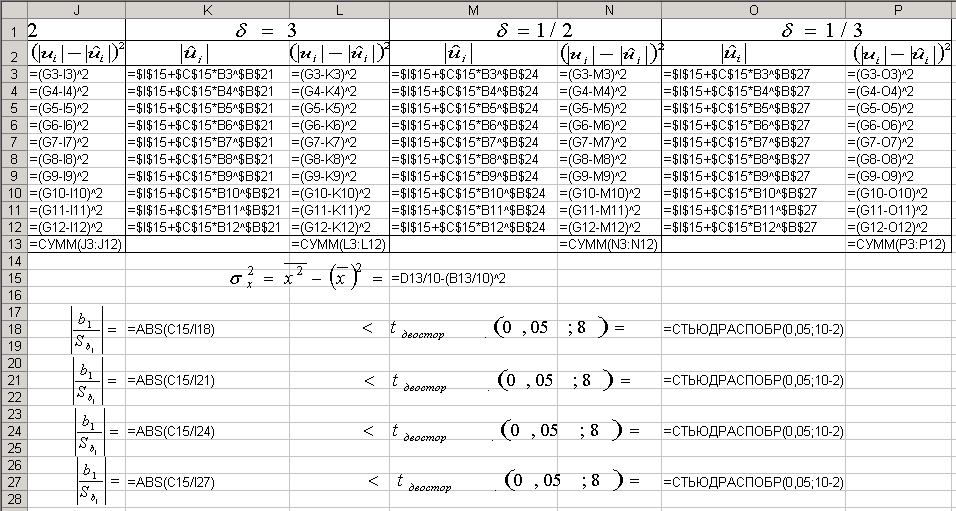
В комірках C15, G15 знайдено МНК-оцінки та . Точкову оцінку невідомої дисперсії збурень знайдено в комірці F18, попередньо обчисливши величини в діапазоні I3:I12. Для цього у комірку I3 вводимо формулу (=$G$15+$C$15*B3^$B$18) з абсолютним посиланнями координат-параметрів b₀, b₁ та і відносним посиланням координати x₁ (а саме B3). Одержану формулу у комірці I3 копіюємо у блок I3:I12. Для визначення значущості порівнюємо знайдені в комірках K18 та O18 величину та t-статистику відповідно.

За аналогією проводимо обчислення для значень , , . Виявляється, що у всіх випадках коефіцієнт регресії незначущий, тобто для статистичних даних задачі передумова 2 виконується.

Матрична форма мнк для оцінки параметрів множинної регресії

Допустимо, що між показником і факторами х₁, х₂ існує лінійна залежність , де , .

Оцінки параметрів вектора шукатимемо за формулу .

Порядок знаходження оцінок параметрів регресії:

1. Знаходимо транспоновану матрицю в блоці по відношенню до матриці в блоці, використовуючи в категорії «Ссылки и массивы» вбудовану функцію ТРАНСП.

2. Знаходимо добуток матриць в виділеному блоці, використовуючи вбудовану математичну функцію МУМНОЖ (блок даних першої матриці; блок даних другої матриці).

3. Обернену матрицю 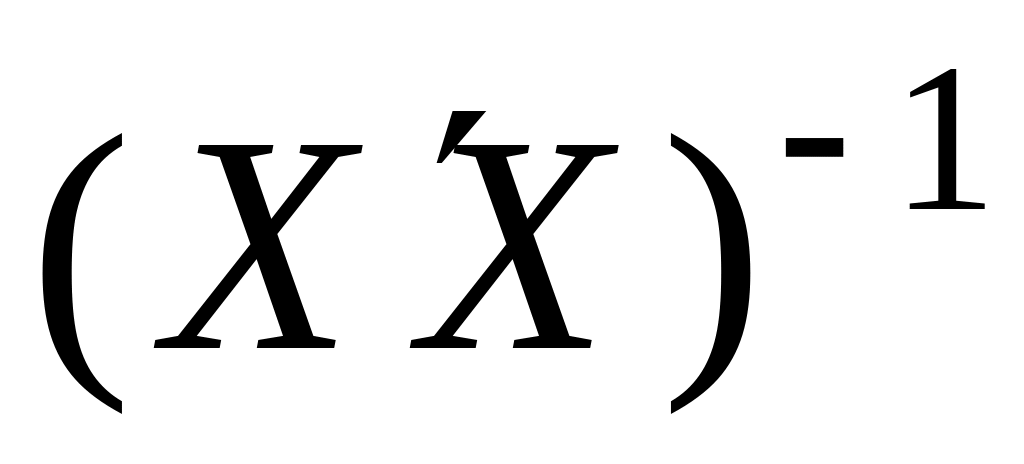знаходимо в іншому виділеному блоці, використовуючи вбудовану математичну функцію МОБР.

4. Добуток матриць знаходимо, використовуючи вбудовану математичну функцію МУМНОЖ, виділивши перед тим масив, в якому буде знайдений добуток матриць.

5. Оцінки вектора знаходимо в виділеному для цього блоці, використовуючи вбудовану математичну функцію МУМНОЖ (блок даних матриці ; блок даних матриці ).

6. Для перевірки значущості параметрів регресії розрахуємо t-статистику кожного із параметрів за формулою

,

де , , — середньоквадратичне відхилення статистичних даних від розрахункових.