
.2 Замена переменных в двойном интеграле
При вычислении двойных интегралов иногда бывает полезно сделать замену переменных. Пусть
![]() (3.13)
(3.13)
функции, определенные на всей плоскости или в некоторой ее области и имеющие непрерывные частные производные в области . Допустим также, что систему уравнений (3.13) можно однозначно разрешить относительно и :
![]() (3.14)
(3.14)
тогда каждой точке
![]() из области
будет взаимно однозначно соответствовать
пара чисел
из области
будет взаимно однозначно соответствовать
пара чисел
![]() ,
называемых криволинейными интегралами
этой точки. Если область
расположена в той части плоскости
,
в которой введены криволинейные
координаты
,
называемых криволинейными интегралами
этой точки. Если область
расположена в той части плоскости
,
в которой введены криволинейные
координаты
![]() ,
,
![]() ,
то справедлива следующая формула:
,
то справедлива следующая формула:
![]() ,
(3.15)
,
(3.15)
где
![]() -
область изменения криволинейных
координат
и
,
отвечающая области
,
а
-
область изменения криволинейных
координат
и
,
отвечающая области
,
а
![]() преобразования (3.14):
преобразования (3.14):
 .
.
В частности, в полярных координатах формула (3.14) имеет вид (рис.14)
![]() (3.16)
(3.16)
Система (3.16)
осуществляет переход от прямоугольных
координат
и
к полярным координатам
![]() и
и
![]() при условии, что полюс помещен в начале
координат и полярная ось направлена
вдоль оси
(рис.15). В этом случае
при условии, что полюс помещен в начале
координат и полярная ось направлена
вдоль оси
(рис.15). В этом случае
![]() фор-
фор-
мула (3.15) принимает вид
![]() .
.

Если область
ограничена лучами, образующими с полярной
осью углы
![]() и
и
![]()
![]() ,
кривыми
,
кривыми
![]() и
и
![]()
![]() (см. рис. 15), то соответствующие этой
области полярные координаты изменяются
в пределах
(см. рис. 15), то соответствующие этой
области полярные координаты изменяются
в пределах
![]() и тогда
и тогда
 .
(3.17)
.
(3.17)
Если область охватывает начало координат, то
![]() ,
(3.18)
,
(3.18)
где
![]() полярное
уравнение кривой, ограничивающее область
(рис.16).
полярное
уравнение кривой, ограничивающее область
(рис.16).
Формулы (3.17) и (3.18) очень удобно использовать при решении задач, когда область есть круг или сектор круга.
Образцы решения задач
Пример 1. Вычислить двойной интеграл
![]() ,
если область
ограничена окружностью
,
если область
ограничена окружностью
![]() (рис.17).
(рис.17).

Решение.
Область
есть круг радиуса 1 с центрами в начале
координат. Введем полярные координаты.
В полярных координатах уравнение
окружности примет вид
![]() ,
или
,
или
![]() (см. формулы (3.18)), т.е.
(см. формулы (3.18)), т.е.
![]() или
или
![]() .
Тогда по формуле (3.18) получаем:
.
Тогда по формуле (3.18) получаем:



![]()
Замечание.
Интеграл
![]() взят методом замены переменной. Положим
взят методом замены переменной. Положим
![]() .
При
.
При
![]() получим
получим
![]() ,
а при
,
а при
![]() .
Изменению переменой
от
.
Изменению переменой
от
![]() до
соответствует изменение переменной
до
соответствует изменение переменной
![]() от
от
![]() до
.
до
.
![]() ,
или
,
или
![]() ,
откуда
,
откуда
![]() .
Подставляя полученные выражения в
интеграл, получим
.
Подставляя полученные выражения в
интеграл, получим![]() .
.
П ример
2. Вычислить
двойной интеграл
ример
2. Вычислить
двойной интеграл
![]() ,
если область
,
если область
![]() ограничена верхней половиной дуги
окружности
ограничена верхней половиной дуги
окружности
![]() и отрезком оси
от точки с абсциссой, равной
и отрезком оси
от точки с абсциссой, равной
![]() до точки с абсциссой, равной
до точки с абсциссой, равной
![]() (рис.18).
(рис.18).
Решение.
Введем полярные координаты. Тогда
уравнение окружности примет вид
![]()
![]()
![]()
![]() или окончательно
имеем
или окончательно
имеем
![]() .
.
Найдем область
определения этой функции. Так как по
определению
![]() ,
то
,
то
![]() ,
то есть
,
то есть
![]() .
Верхняя часть дуги окружности лежит в
первой четверти, для которой
меняется в пределах от
до
.
Верхняя часть дуги окружности лежит в
первой четверти, для которой
меняется в пределах от
до
![]() .
По формуле (3.17) имеем
.
По формуле (3.17) имеем
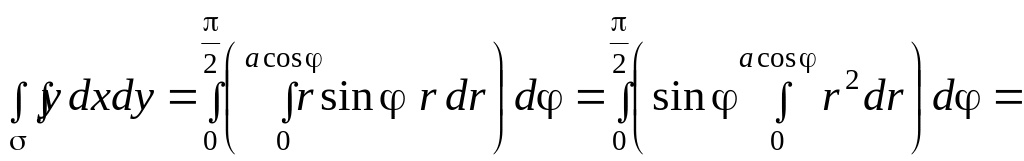


Пример 3.
Вычислить объем тела, ограниченного
плоскостью
![]() и параболоидом
и параболоидом
![]() (рис.19).
(рис.19).
Решение. Сверху данное тело (см.рис.19) ограничено параболоидом , поэтому, воспользовавшись формулой (3.10) для вычисления объема цилиндрического тела, ограниченного плоскостью плоскости , имеем
![]()

Область
(рис.20) есть круг, его границу получим
подстановкой
в уравнение
![]() .
.
Введем полярные
координаты. Тогда уравнение окружности
примет вид
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Угол
меняется от
до 2
.
Угол
меняется от
до 2![]() .
.
Учитывая симметрию
тела относительно плоскостей
![]() и
и
![]() ,
воспользовавшись формулой (3.10) , найдем:
,
воспользовавшись формулой (3.10) , найдем:



![]()
Следовательно,
![]() .
.
Пример 4. Вычислить двойной интеграл
![]() ,
если область
ограничена линиями: дугой окружности
,
если область
ограничена линиями: дугой окружности
![]() и прямыми
и прямыми
![]() ,
,
![]() .
.
![]() (рис.21).
(рис.21).
 Решение.
Введем полярные координаты. Тогда
уравнение окружности примет вид:
Решение.
Введем полярные координаты. Тогда
уравнение окружности примет вид:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найдем угол между
прямой
и осью
.
В полярных координатах уравнение прямой
примет вид:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Значит угол между
прямой
и осью
равен
![]() .
Найдем угол между прямой
.
Найдем угол между прямой
![]() и осью
.
В полярных координатах данное уравнение
примет вид:
и осью
.
В полярных координатах данное уравнение
примет вид:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Значит угол равен
.
Значит угол равен
![]() .
.
Таким образом
получим пределы изменения угла
от
до
![]() .
По формуле (3.17) имеем:
.
По формуле (3.17) имеем:





Вариант №1 Вычислить
1)
3)
4)
5)
6)
Вариант №3 Вычислить 1) 3) 4) 5)
6)
Вариант №5 Вычислить
1) 3) 4)
5)
6)
Вариант №7 Вычислить 1) 3) 4) 5) 6)
Вариант №9 Вычислить 1) 3) 4) 5) 6)
Вариант №12 Вычислить 1) 3) 4) 5) 6) Вариант №14 Вычислить 1) 3)
4) 5) 6)
Вариант №16 Вычислить
1)
3)
4)
5)
6) Вариант №18
1)
3)
4)
5)
6)
Вариант №20
1)
3)
4)
5)
6)
Вариант №22
1)
3)
4)
5)
6)
Вариант №24
1)
3)
4)
5)
6)
|
Вариант №2 Вычислить 1) 3)
4)
5)
6)
Вариант №4 Вычислить
1) 3) 4) 5) 6)
Вариант №6 Вычислить 1) 4) 5)
6)
Вариант №8 Вычислить 1) 3) 4) 5) 6) Вариант №10 Вычислить 1) 3) 4) 5)
6)
Вариант №11 Вычислить 1) 3) 4) 5) 6) Вариант №13 Вычислить 1) 3) 4) 5) 6) Вариант №15 Вычислить 1) 3) 4) 5)
7) Вариант №17 Вычислить
1)
3) 4) 5)
Вариант №19
1)
3)
4)
5)
6)
Вариант №21
1)
3)
4)
5) 5.
6)
Вариант №23 1) 2) 3)
4)
5)
6)
Вариант №25 Вычислить 1) 3) 4) 5) 6)
|


 2)
2)


 2)
2)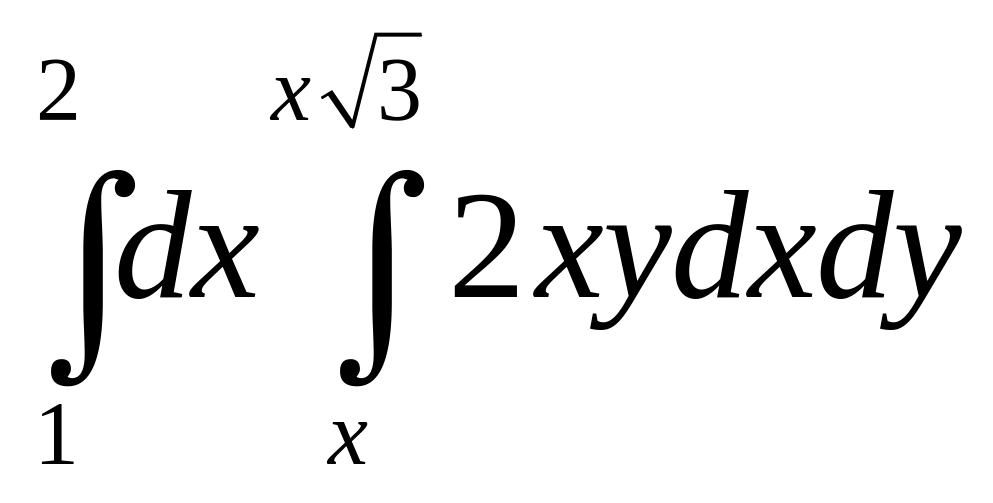


 2)
2)

 2)
2)


 I-четверть
I-четверть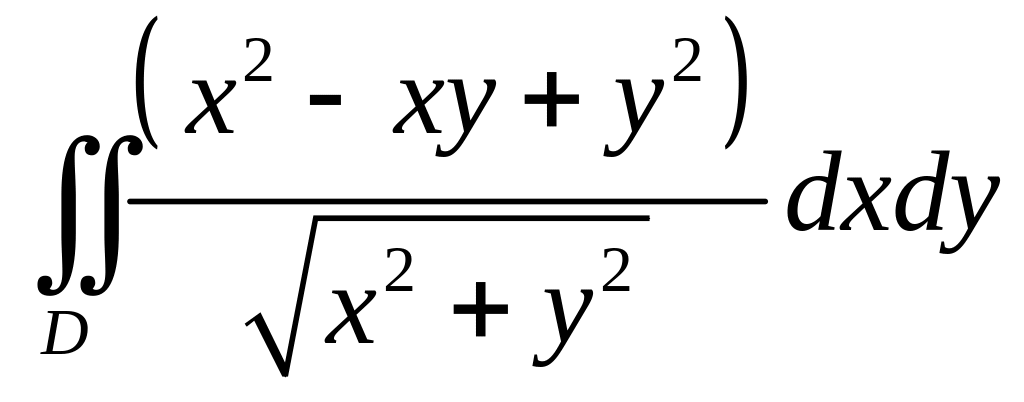
 I-четверть
I-четверть



 2)
2)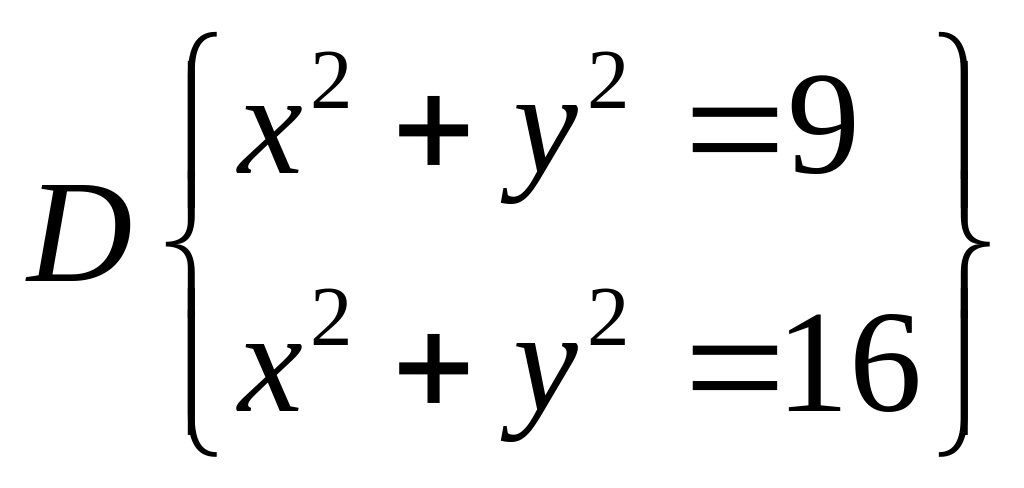


 I-четверть
I-четверть III -четверть
III -четверть