§3. Поўныя сістэмы злучнікаў
Як было адзначана вышэй, кожная прапазiцыйная формула, у якую ўваходзяць лiтараў, вызначае булеву функцыю ад аргументаў. Логiкава эквiвалентным формулам адпавядае тая сама булева функцыя. Натуральна паўстае пытанне: цi ўсе булевы функцыi спараджаюцца такiм чынам?
Сцверджанне 1. Кожная булева функцыя спараджаецца некаторай прапазiцыйнай формулай, якая мае злучнiкi , і .
Доказ.
Няхай
–
булева функцыя. Задамо
таблiцай з
радкоў, дзе кожны радок змяшчае пэўнае
размеркаванне значэнняў зменных
i адпаведнае значэнне
.
Занумаруем радкi гэтай таблiцы лiкамi
.
Няхай для кожнага
,
дзе
ёсць
,
калi
ў
-м
радку таблiцы
мае значэнне 1, i
ёсць
,
калi
мае значэнне 0. Абазначым праз
дыз’юнкцыю ўсiх
такiх,
што функцыя
у
-м
радку таблiцы
мае значэнне 1 (калi
такiх
радкоў няма, тады формула
спараджае функцыю
,
i
ў гэтым выпадку сцверджанне даказанае).
Булева функцыя, спароджаная формулай
,
роўная
.
Сапраўды, няхай некатораму размеркаванню
значэнняў лiтараў
адпавядае
-ты
радок.
мае пры гэтым размеркаваннi значэнне
1, усе астатнiя
–
0. Калi для
-га
радка
мае значэнне 1, тады
з’яўляецца дыз’юнкцыйным складнiкам
i, значыць,
пры гэтым размеркаваннi мае значэнне
1. Калi ж для
-га
радка
мае значэнне 0, тады
не з’яўляецца дыз’юнкцыйным складнiкам
i, значыць,
набывае
значэнне 0. Такiм чынам, спароджаная
формулай
булева
функцыя ёсць
.
■
З сцверджання 1 вынiкае, што вывучэнне прапазiцыйных формулаў з дакладнасцю да логiкавай эквiвалентнасцi раўназначнае вывучэнню булевых функцыяў.
Вынiк 1. Для кожнай з наступных трох параў злучнiкаў: і , і , і і для ўсякай булевай функцыi iснуе прапазiцыйная формула, якая змяшчае злучнiкi толькi з гэтай пары i спараджае .
Доказ. Формула
логiкава эквiвалентная
(праверце гэта!), таму няцяжка зразумець,
што ўсякая прапазiцыйная формула, якая
змяшчае толькi злучнiкi
,
і
,
логiкава эквiвалентная некаторай
прапазiцыйнай формуле, якая змяшчае
толькi злучнiкi
і
(формуле,
атрыманай заменай выразаў
на
.
Астатнiя сцверджаннi вынiку атрымлiваюцца
з логiкавых эквiвалентнасцяў:
;
(дакажыце iх!). ■
Увядзем два новыя
злучнiкi
(кан’юнкцыя
адмаўленняў)
i
(дыз’юнкцыя
адмаўленняў, або
штрых Шэфера)
формуламi:
,
.
Вынiк 2. Для кожнага з злучнiкаў i i для ўсякай булевай функцыi iснуе прапазiцыйная формула, якая змяшчае толькi адзiн гэты злучнiк i спараджае .
Доказ. Сцверджанне атрымлiваецца з вынiку 1 i эквiвалентнасцяў
,
,
,
.
■
З сцверджання 1 вынiкае, што кожная прапазiцыйная формула логiкава эквiвалентная формуле, якая з’яўляецца дыз’юнкцыяй некалькіх (магчыма, аднаго) дыз’юнкцыйных складнiкаў, кожны з якiх ёсць кан’юнкцыя адной або некалькiх лiтараў ці iх адмаўленняў; такая формула называецца дыз’юнкцыйнай нармальнай формай (ДНФ) формулы . Доказ сцверджання 1 дае наступнае правiла пабудовы гэтай ДНФ:
1) пiшам таблiцу праўдзiвасцi прапазiцыйнай формулы;
2) выбiраем радкi, у якiх формула мае значэнне 1;
3) для кожнага вылучанага радка лiтары, якiя ўваходзяць у формулу, злучаем кан’юнкцыяй, прычым лiтару бярэм з адмаўленнем, калi яе значэнне ў гэтым радку 0, i без адмаўлення, калi яе значэнне 1;
4) атрыманыя кан’юнкцыi лiтараў або iхнiх адмаўленняў злучаем дыз’юнкцыяй.
Формула, якая з’яўляецца кан’юнкцыяй некалькіх (магчыма, аднаго) кан’юнкцыйных складнiкаў, кожны з якiх ёсць дыз’юнкцыя адной або некалькiх лiтараў ці iх адмаўленняў, логікава эквівалентная прапазіцыйнай формуле , называецца кан’юнкцыйнай нармальнай формай (КНФ) формулы .
Прыклад 1.
,
,
,
,
,
- ДНФ,
,
,
,
,
,
- КНФ.
Прыклад 2.
Для таго, каб знайсцi ДНФ формулы
,
напiшам таблiцу праўдзiвасцi гэтай формулы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
* |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
* |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
* |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
* |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
* |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
* |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
* |
Затым, паводле правiла пабудовы ДНФ, знаходзiм шуканую формулу:
.
Практыкаваннi. 1. Даказаць, што для кожнай прапазiцыйнай формулы існуе КНФ. (Парада. Разгледзець адмаўленне дадзенай прапазiцыйнай формулы i ДНФ гэтага адмаўлення).
2. Сфармуляваць правiла пабудовы КНФ для прапазiцыйнай формулы, скарыстаўшы практыкаванне 1 i правiла пабудовы ДНФ.
3. Знайсцi КНФ i ДНФ формулаў:
(1)
;
(2)
;
(3)
;
(4)
;
(5) .
4.
Даказаць, што кожная з параў злучнiкаў
i
не з’яўляецца дастатковай для выражэння
адвольнай булевай функцыi.
5. Даказаць, што адзiнымi бiнарнымi злучнiкамi, кожнай з якiх дастаткова для выражэння ўсiх булевых функцыяў, з’яўляюцца злучнiкi і .
6. Некаторая краiна населеная жыхарамi, кожны з якiх або заўсёды кажа праўду, або заўсёды манiць, i якiя на ўсе пытаннi адказваюць “так” або “не”. Да скрыжавання дарог, адна з якiх вядзе ў сталiцу краiны, а другая – не, прыйшоў вандроўнiк. Нiякiх шыльдаў, што паказваюць, якая з дарог куды вядзе, на ростанi няма. Але тут стаiць тутэйшы чалавек. Якое пытанне мусiць задаць яму падарожнiк, каб вызначыць, якая дарога вядзе ў сталiцу (пытанне павiнна быць такiм, каб на яго можна было адказаць “так” або “не”)? (Парада. Няхай – выказванне “Вы заўсёды кажаце праўду”, а – “Левая дарога вядзе ў сталiцу”. З дапамогаю таблiцы праўдзiвасцi пабудаваць такую прапазiцыйную формулу ад лiтараў i , каб адказ тутэйшага чалавека на пытанне, цi праўдзiвае выказванне, адпаведнае гэтай формуле, быў “так” калi i толькi калi праўдзiвае.)
Прыклад 3.
Разгледзiм
электрычны ланцуг, паказаны на мал.1.
Ланцуг мае кантакты, абазначаныя лiтарамi
;
кантакты, абазначаныя адной лiтарай,
падключаныя да аднаго рэле (пераключальнiка),
г.зн., замыкаюцца i размыкаюцца адначасова.
Калi рэле замыкае кантакт, ток праз яго
праходзiць, калi размыкае –
не праходзiць. Кантакт, абазначаны
,
падключаны да таго сама рэле, што i
,
прычым ток праз яго праходзiць калi i
толькi калi праз
не праходзiць. Такiя электрычныя ланцугi
будзем называць кантактнымi
схемамi.
Спрасцiм гэты ланцуг, г.зн. паспрабуем
пабудаваць эквiвалентную кантактную
схему, якая мае меншую колькасць кантактаў
(дзве кантактныя схемы называюцца
эквiвалентнымi,
калi праз адну з iх ток iдзе калi i толькi
калi ён iдзе праз другую).
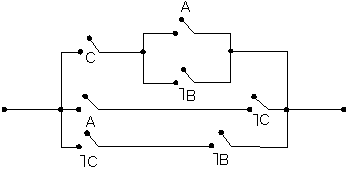
Мал. 1
Кожнай электрычнай
схеме, якая мае толькi такiя кантакты,
пры адным стане якога ток праз яго
праходзiць, а пры iншым –
не, можна паставiць у адпаведнасць булеву
функцыю ад зменных, што адпавядаюць
розным рэле, наступным чынам. Зменная,
якая абазначае пэўны кантакт, набывае
значэнне 1, калi адпаведнае рэле замыкае
кантакт, i 0, калi рэле размыкае кантакт;
булева функцыя, адпаведная кантактнай
схеме, набывае значэнне 1, калi схема
праводзiць ток, i 0 у адваротным выпадку.
Такую булеву функцыю будзем называць
функцыяй
праводнасцi кантактнай
схемы. Напрыклад, функцыя праводнасцi
кантактнай схемы, адлюстраванай на
мал.1, задаецца наступнай таблiцай:
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Гэтай булевай функцыi адпавядае прапазiцыйная формула
.
Дастасаваўшы
да
гэтай
прапазiцыйнай
формулы
логiкавыя
эквiвалентнасцi
(2), (8) з
практыкавання
5 §2, атрымаем,
што
яна
эквiвалентна
прапазiцыйнай
формуле
,
,
і, нарэшце,
(бо
паводле
прыкладу
4 таго
ж
параграфу
–
таўталогiя).
Вiдавочна,
што
эквiвалентным
кантактным
схемам
адпавядаюць
эквiвалентныя
прапазiцыйныя
формулы,
таму
электрычны
ланцуг,
адлюстраваны
на
мал.1,
будзе
эквiвалентны
электрычнаму
ланцугу,
паказанаму
на
мал.2.
Мал. 2
Прыклад 4. Пабудаваць схему з трыма пераключальнiкамi, якая замыкаецца калi i толькi калi замкнёныя або адзiн, або два пераключальнiкi. Пры пабудове ўжывайце не больш за шэсць кантактаў.
Электрычнай схеме, якую трэба пабудаваць, адпавядае функцыя праводнасцi ад трох зменных з таблiцай
|
|
|
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
Па таблiцы пабудуем КНФ, якая вызначае гэтую булеву функцыю (гл. практыкаванне 2):
.
Гэтай формуле адпавядае электрычны ланцуг
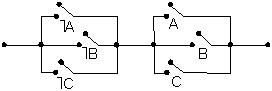
Мал. 3
якi задавальняе ўмову задачы.
Практыкаваннi. 7. Па кантактнай схеме знайсцi яе функцыю праводнасцi:
(1)
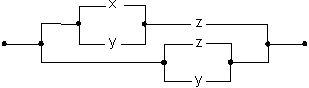
(2)
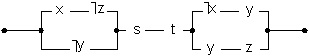
(3)
8. Пaбудаваць кантактную схему, адпаведную прапазіцыйнай формуле:
(1)
;
(2)
;
(3)
.
9. Спрасцiць кантактныя схемы:
(1)
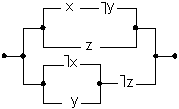
(2)
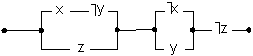
(3)
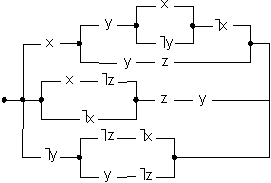
(4)
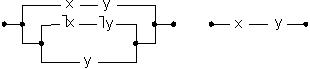
10. Праверыць раўназначнасць кантактных схемаў:
(1)
(2)
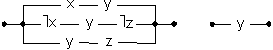
(3)
11. Камiтэт складаецца з трох чалавек, кожны з якiх галасуе “за”, нацiскаючы на гузiк. Пабудаваць па магчымасцi найпрасцейшы ланцуг, праз якi ток праходзiў бы калi i толькi калi не менш за два сябры камiтэту галасуюць “за”.
12. Трэба, каб святло ў пакоi ўключалася адным з трох пераключальнiкаў такiм чынам, каб нацiсканне на адвольны з iх прыводзiла да ўключэння святла, калi яно было перад гэтым выключана, i да выключэння, калi яно было ўключанае. Пабудаваць электрычны ланцуг, якi адпавядае гэтай умове.