
4.17.1.Дифференциальные и интегральные зависимости при изгибе
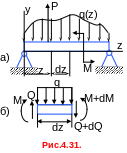
Рассмотрим произвольно нагруженную балку (рис.4.31,а), где положительное направление распределенной нагрузки q(z) совпадает с положительным направлением оси y. Для элементарного участка dz балки в пределах действия только нагрузки q учтем возникающие в сечениях внутренние силовые факторы (рис.4.31,б). В пределах малого участка dz нагрузку q можно считать равномерно распределенной, M и Q приложены в положительном направлении с учетом их изменении по длине.
Уравнения равновесия выделенной части балки имеют вид (для уравнения моментов поперечная ось x рассматривается для правого сечения)
![]()
 ;
;
![]() ;
;
![]() ;
;
![]() .
.
Отбрасывая во втором уравнении слагаемые второго порядка малости, получаем дифференциальные уравнения при изгибе
![]() ;
;
![]() ;
;
![]() .
.
Из последних соотношений путем интегрирования можно получить интегральные зависимости при изгибе
![]() ,
,
![]() ,
где Q0
и M0
- значения поперечной силы и изгибающего
момента в начальном сечении участка.
,
где Q0
и M0
- значения поперечной силы и изгибающего
момента в начальном сечении участка.
4.17.2. Чистый изгиб.
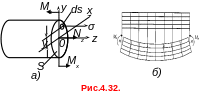 При
чистом изгибе продольные линии и ось
стержня примут форму дуг окружности,
а поперечные линии останутся прямыми.
Поэтому при чистом изгибе справедливы
следующие гипотезы:
При
чистом изгибе продольные линии и ось
стержня примут форму дуг окружности,
а поперечные линии останутся прямыми.
Поэтому при чистом изгибе справедливы
следующие гипотезы:
плоские поперечные сечения останутся плоскими и после деформации (гипотеза плоских сечений),
продольные слои балки не взаимодействуют друг с другом, т.е. нормальные напряжения в продольных сечениях равны нулю.
Деформации и напряжения по ширине поперечного сечения балки постоянны.
При прямом чистом изгибе в поперечном сечении стержня возникает только один силовой фактор — изгибающий момент Мх (рис.4.32,а). Так как Qy=dMx/dz=0, то Mx=const и чистый прямой изгиб может быть реализован при нагрузке стержня парами сил, приложенными в торцевых сечениях стержня.
Поскольку изгибающий момент Mх по определению равен сумме моментов внутренних сил относительно оси Ох с нормальными напряжениями его связывает выкающее из этого определения уравнение статики
![]() .
.
Рассмотрим
деформацию модели стержня из материала,
на боковой поверхности которого нанесена
сетка продольных и поперечных рисок
(рис.4.32,б). Поперечные риски при изгибе
стержня парой сил, приложенными в
торцевых сечениях, остаются прямыми и
перпендикулярными к искривленным
продольным рискам. Это позволяет сделать
вывод о выполнении гипотезы
плоских сечений,
которая в теории упругости становится
законом
плоских сечений.
Замеряя изменение расстояний между
продольными рисками, приходим к выводу
о справедливости гипотезы о сдавливании
(растяжении) продольных волокон. При
этом
![]() .
.
Ортогональность продольных и поперечных рисок до и после деформирования указывает на отсутствие сдвигов, касательных напряжений в поперечных и продольных сечениях стержня.
Таким
образом, чистый прямой изгиб призматического
стержня сводится к одноосному растяжению
или сжатию продольных волокон напряжениями
![]() .
При этом часть волокон находится в зоне
растяжения (на рис.4.31,б это нижние
волокна), а другая часть—в зоне сжатия
(верхние волокна).
.
При этом часть волокон находится в зоне
растяжения (на рис.4.31,б это нижние
волокна), а другая часть—в зоне сжатия
(верхние волокна).
Существует слой, в котором удлинения и сжатия отсутствует, его называют нейтральным слоем или нейтральной линией. Эта линия, как правило, проходит по оси стержня.
