11.2. Математическая модель генетического алгоритма

Генетический алгоритм работает с представленными в конечном алфави­те строками S конечной длины 1, которые используются для кодировки исходного множества альтернатив W. Строки представляют собой упорядоченные наборы из 1 элементов:каждый из которых может быть задан в своем собственном алфавите где алфавит V_i является множеством из Г; символов:

Для решения конкретной задачи требуется однозначно отобразить конечное множество альтернатив W на множество строк подходящей длины

(очевидно, что длина строк зависит от алфавитов, используемых для их задания).

Для работы алгоритма необходимо на множестве строк задать неотрицательную функцию F(S), определяющую показатель качества, «ценность» строкиАлгоритм производит поиск строки, для

которой

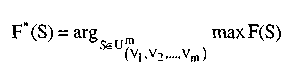
Если на множестве W задана целевая функция f(w), то функцию F(S) на множестве строк можем определить следующим образом:

если элемент w при отображении исходного множества W на множество строк был сопоставлен строке S.

Генетический алгоритм за один шаг производит обработку некоторой по­пуляции строк. Популяция G(t) на шаге t представляет собой конечный на­бор строк

:

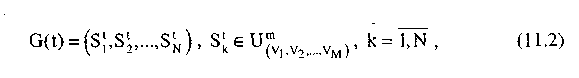
где N— размер популяции, причем строки в популяции могут повторяться.

Анализ работы алгоритма удобно производить, используя аппарат шим. Шимой в генетическом алгоритме называют описание некоторого подмно­жества строк. Шима H=(h₁ h₂, ..., h_m) может рассматриваться как строка, алфавиты для элементов которой дополнены специальным символом «#»:

Если в некоторой позиции r шимы Н присутствует символ «#», то такая позиция называется свободной, а сам символ «#» интерпретируется как произвольный символ из алфавита V_r. Позиция q шимы Н называется фик­сированной, если в этой позиции присутствует один из символов алфавита V_q. Шима Н, в которой определены фиксированные и свободные позиции,

описывает подмножествосодержащее такие строки, у

которых элементы, соответствующиефиксированным позициям шимы,совпадают с символами шимы, а элементы, соответствующие свободным позициям шимы, являются произвольно заданными в соответствующих алфавитах:

где— множество целых чисел отрезка [1, т]. Например, для множества строкзадает

такое множество строк, у которых первым элементом является символ «1», пятым — «О», а остальные — либо «О», либо «1». Строки «10010», «11110» являются примерами строк, принадлежащих множеству U_Н1 . Часть попу­ляциистроки которой удовлетворяют шиме Н, обозна­чают

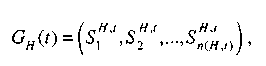
где n(H, t) — число строк шимы Н в популяции G(t) и называют подпопуляцией, соответствующей шиме Н.

Суть генетического алгоритма заключается в следующем. Пусть на шаге t имеется популяция G(t), состоящая из N строк. Для популяции вводится по­нятие средней ценности популяции

Аналогично для подпопуляции Gn(t), удовлетворяющей шиме Н, вводит­ся понятие средней ценности подпопуляции

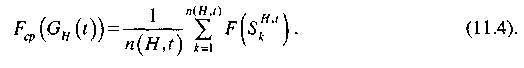
Генетический алгоритм осуществляет переход от популяции G(t) к популяции G(t+1) таким образом, чтобы средняя ценность составляющих ее строк увеличивалась, причем количество новых строк в популяции равно КЧ N, где К— коэффициент новизны. Если К<1, то популяция будет перекрывающейся, т.е. в новой популяции сохраняются некоторые строки из старой, а если К=1, то она будет не перекрывающейся, т.е. подвергнется полному обновлению.

Генетический алгоритм включает три операции: воспроизводство, скрещивание, мутация.

Воспроизводство представляет собой процесс выбора K*N N строк по­пуляции G(t) для дальнейших генетических операций. Выбор производится случайным образом, причем вероятность выбора строки S_i¹ пропорциональна ее ценности:

Процесс выбора повторяется K*N N раз. Предполагаемое количество экземпляров строки S_i¹ в популяции

Операция воспроизводства увеличивает общую ценность последующей популяции путем увеличения числа наиболее ценных строк.

Пусть в популяции G(t) содержится n(H, t) строк, удовлетворяющих шиме Н. Тогда в результате воспроизводства количество строк, удовлетворяю­щих шиме Н в популяции G(t+1), будет равно n(H, t+1):

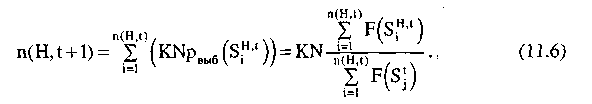
Используя выражения для средней ценности популяции F_cp(G(t)) и подпопуляцииможно записать формулу (11.3) в виде:

Средняя ценность подпопуляции, соответствующей шиме Н, может быть представлена в следующем виде:

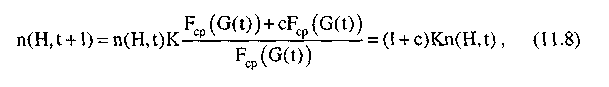
где с — некоторая величина. Тогда формула (11.8) примет вид:

Предположим, что величина с при изменении t не изменяется; тогда, на­чиная с t=0, получим:

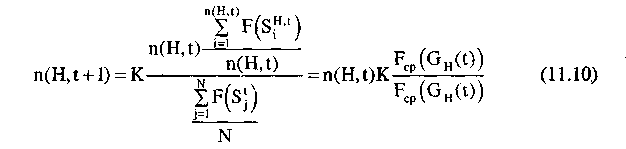
т.е. в этом случае число представителей шимы (строк популяции G(t), соот­ветствующих шиме) изменяется в геометрической прогрессии. В общем слу­чае можно сказать, что процесс изменения представителей шимы так же аппроксимируется геометрической прогрессией.

Таким образом, в результате операции воспроизводства те шимы, для ко­торых соответствующие подпопуляции имеют среднюю ценность выше средней в популяции, увеличивают количество своих представителей.

Воспроизводство оперирует со строками, уже присутствующими в рассматриваемой популяции, и само по себе не способно открывать новые области поиска. Для этой цели используется операция скрещивания.

Скрещивание представляет собой процесс случайного обмена значения­ми соответствующих элементов для произвольно сформированных пар строк. Для этого выбранные на этапе воспроизводства строки случайным образом группируются в пары. Далее каждая пара с заданной вероятностью р_скр подвергается скрещиванию. При скрещивании происходит случайный выбор позиции разделителя— длина строки). Затем значения первых d элементов первой строки записываются в соответствую­щие элементы второй, а значения первых d элементов второй строки— в соответствующие элементы первой. В результате получаем две новых стро­ки, каждая из которых является комбинацией частей двух родительских строк. Операция скрещивания создает новые строки путем некоторой ком­бинации значений элементов наиболее ценных в популяции G(t) строк. По­лучившиеся в результате строки могут превосходить по ценности родитель­ские строки.

Рассмотрим некоторую шиму Н, для которой определим порядок о(Н) — число фиксированных позиций шимы и определяющую длину d (H) - рас­стояние (число позиций) между первой и последней фиксированными пози­циями. Допустим, что до операции скрещивания строка S была представите­лем шимы. Допустим, что строкаS1 получена из строки S в результате скрещивания. Строка S₁ будет представителем шимы Н в том случае, если позиция разделителя при скрещивании не располагалась между фиксированными позициями шимы. Вероятность того, что позиция раздели­теля окажется между фиксированными позициями шимы, равна:

Полагая независимость операций воспроизводства и скрещивания, оце­ним совокупный эффект от этих операций, т.е. число представителей шимы Н в популяции

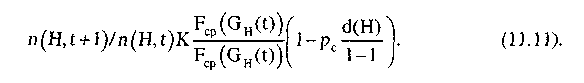
Так как открытие новых областей поиска в операции скрещивания про­исходит лишь путем перегруппирования имеющихся в популяции комбина­ций символов, то при использовании только этой операции некоторые по­тенциально оптимальные области могут оставаться нерассмотренными. Для предотвращения подобных ситуаций применяется операция мутации.

Мутация представляет собой процесс случайного изменения значений элементов строки. Для этого строки, получившиеся на этапе скрещивания, просматриваются поэлементно, и каждый элемент с заданной вероятностью мутации р_мут может мутировать, т.е. изменить значение на любой случайно выбранный символ, допустимый для данной позиции. Операция мутации позволяет находить новые комбинации признаков, увеличивающих ценность строк популяции.

Допустим, что до мутации строка S1 была представителем шимы Н, т.е. Допустим, что строка S2 получена из строки S1 в результате мутации. Строка S2 будет представителем шимы Н в том случае, если ни один из элементов строки, соответствующий фиксированным позициям шимы, не был изменен.

Учитывая, что мутация происходит с вероятностью р_мут, вероятность p_s2 того, что строка S2 является представителем шимы Н, определяется выра­жением:—

число фиксированных позиций ши­мы Н.

Полагая независимость операций воспроизводства, скрещивания и мута­ции оценим совокупный эффект от этих операций, т.е. число представителей шимы Н в популяции G(t+1):

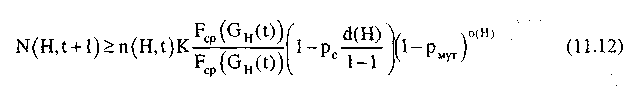
Так как при малых значениях рm приближенно можно считать;

то выражение (11.12) можно записать в виде:

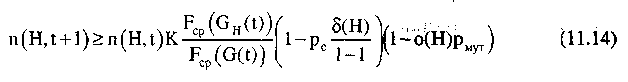
или

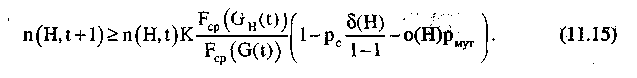
Таким образом, шимы, у которых малы определяющая длина и порядок, и для которых соответствующая подпопуляция имеет среднюю ценность, -превышающую среднюю ценность популяции, экспоненциально увеличива­ют число представителей в последующих поколениях.

Очевидно, что эффективность описанной операции скрещивания значительно зависит от способа кодировки строк. Это свойство оказывается по­лезным для задач оптимизации функций, заданных на числовых множествах. Однако если функция задана на произвольном множестве, например на множестве комбинаций значений признаков объекта, где все признаки одинаковы по предпочтительности, то описанный выше способ скрещивания оказывается не вполне корректным, так как вероятность сохранения значе­ний для групп признаков зависит от расстояния между элементами группы в кодовой строке, а это нарушает принцип равной предпочтительности признаков.

Поэтому для таких задач операцию скрещивания предполагается производить путем обмена не частями строк, а отдельными элементами. При этом задается некоторое число позиций которое определяет количество элементов строк, для которых производится обмен значениями. Число позиций n_п может быть задано непосредственно или определяться случайно для каждой пары строк. Далее для каждой пары строк (S1, S2)_i, где i — номер пары, случайно выбираются n_п номеров Затем для строк пары (S1, S2)_i производится обмен значения­ми элементов с номерами n_ij т.е. каждому элементу с номером n_ij строки S1 присваивается значение элемента с номером n_ij строки S2, а элементу с но­мером n_ij строки S2 присваивается значение элемента с номером n_ij строки S1.

Допустим, что до операции скрещивания строка S была представителем шимыа строка S1 получена из строки S в результате поэлементного скрещивания. Вероятность p_ij того, что строка S1 будет представи­телем шимы Н, равна: — число фиксирован­ных позиций шимы Н.

Совокупный эффект от операций воспроизводства и поэлементного скрещивания и мутации, т.е. число представителей шимы Н в популяции G(t+1), определяется выражением:

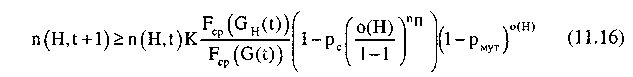
Таким образом, при поэлементном скрещивании скорость увеличения представителей шимы в последующих поколениях зависит от средней цен­ности шимы и количества фиксированных позиций и не зависит от расстоя­ния между ними, а значит, не зависит от порядка расположения элементов в строке.

Итак, в результате описанных выше операций получаем KNN новых строк, которые либо полностью формируют новую популяцию G(t+1) (при К=1), заменяя при этом все строки популяции G(t), либо составляют часть популяции G(t+1), заменяя собой KNN наименее ценных строк предыдущей популяции. Как видно из описания алгоритма, закон вероятности распределения значений целевой функции определяется и корректируется путем использования набора (популяции) строк, содержащих наилучшие в смысле значений целевой функции ком­бинации элементов.

Таким образом, на каждой итерации генетического алгоритма, называе­мом также поколением, имеется предетерминированное число выживших «индивидуумов», каждый из которых представляет отдельное решение. Индивидуумы представляются цепочками или векторами. В контексте обучения машины элементы таких цепочек являются, вообще говоря, переменны­ми, оптимизирующими критерий. Новые цепочки генерируются посредст­вом использования генетических операторов, включая «кроссовер», инвер­сию и мутацию. Операция кроссовера сцепляет пару выживших индивидуу­мов в случайно выбранной точке и имеет у них местами два «хвоста», т.е. части векторов, находящиеся ниже точки сцепления.

Инверсия заменяет одну часть цепочки ее дополнением.

Мутация выражается в случайной инверсии одного или более элементов цепочки одного или более индивидуалов. Хотя появление совершенных или «оптимальных» индивидуалов не гарантировано, популяция выживших индивидуумов будет в среднем показывать все более точные оценки в каждом последующим поколении.

Возвращаясь к задаче оптимального распределения инвестиций, поясним особенности реализации генетического алгоритма в этом случае.

• Индивидуум = вариант решения задачи = набор из 10 хромосом X_j.

• Хромосома X_j = объем вложения в проект j = 16-разрядная запись этого числа.

• Так как объемы вложений ограниченны, не все значения хромосом явля­ются допустимыми. Это учитывается при генерации популяций.

• Так как суммарный объем инвестиций фиксирован, то реально варьиру­ются только 9 хромосом, а значение 10-й определяется по ним однознач­но.

Генетический алгоритм представляет собой комбинированный метод. Механизмы скрещивания и мутации в каком-то смысле реализуют перебор­ную часть метода, а отбор лучших решений— градиентный спуск. На ри­сунке показано, что такая комбинация позволяет обеспечить устойчиво хо­рошую эффективность генетического поиска для любых типов задач.

Итак, если на некотором множестве задана сложная функция от нескольких переменных, то генетический алгоритм — это программа, которая за разумное время находит точку, где значение функции достаточно близко к максимально возможному. Выбирая приемлемое время расчета, мы получим одно из лучших решений, которые вообще возможно получить за это время.

Структура данных генетического алгоритма состоит из одной или боль­шего количества хромосом (обычно из одной). Как правило, хромосома — это битовая строка, так что термин «строка» часто заменяет понятие «хромо­сома». В принципе, генетические алгоритмы не ограничены бинарным пред­ставление. Известны другие реализации, построенные исключительно на векторах вещественных чисел. Несмотря на то, что для многих реальных задач, видимо, больше подходят строки переменной длины, в настоящее время структуры фиксированной длины наиболее распространены и изуче­ны.

Каждая хромосома (строка) представляет собой конкатенацию ряда под­компонентов, называемых генами. Гены располагаются в различных позици­ях или локусах хромосомы, и принимают значения, называемые аллелями. В представлениях с бинарными строками, ген — бит, локус — его позиция в строке, и аллель — его значение (0 или 1). Биологический термин «генотип» относится к полной генетической модели особи и соответствует структуре в генетическом алгоритме. Термин «фенотип» относится к внешним наблю­даемым признакам и соответствует вектору в пространстве параметров. Чрезвычайно простой, но иллюстративный пример — задача максимизации следующей функции двух переменных:

Обычно методика кодирования реальных переменных x₁ и х₂ состоит в их преобразовании в двоичные целочисленные строки достаточной длины — достаточной для того, чтобы обеспечить желаемую точность. Предположим, что 10-разрядное кодирование достаточно и для х₁ и х₂. Установить соответствие между генотипом и фенотипом закодированных особей можно, разде­лив соответствующее двоичное целое число— на 2¹⁰-1. Например, 0000000000 соответствует 0/1023 или 0, тогда как 1111111111 соответствует 1023/1023 или 1. Оптимизируемая структура данных— 20-битная строка, представляющая конкатенацию кодировок х₁ и х₂. Переменная x₁ размещает­ся в крайних левых 10-разрядах, тогда как х₂ размещается в правой части генотипа особи (20-битовой строке). Генотип — точка в 20-мерном хеммининговом пространстве, исследуемом генетическим алгоритмом. Фенотип — точка в двумерном пространстве параметров.

Чтобы оптимизировать структуру, используя генетические алгоритмы, нужно задать некоторую меру качества для каждой структуры в простран­стве поиска. Для этой цели используется функция приспособленности. В функциональной максимизации целевая функция часто сама выступает в качестве функции приспособленности (например, наш двумерный пример); для задач минимизации, целевую функцию следует инвертировать и сме­стить затем в область положительных значений. Простой генетический ал­горитм случайным образом генерирует начальную популяцию структур. Работа генетического алгоритма представляет собой итерационный про­цесс, который продолжается до тех пор, пока не выполнятся заданное чис­ло поколений или какой-либо иной критерий остановки. На каждом поко­лении генетического алгоритма реализуется отбор пропорционально приспособленности, одноточечный кроссовер и мутация. Сначала пропорциональный отбор назначает каждой структуре вероятность Ps(i) равную отношению ее приспособленности к суммарной приспособленности популя­ции.

Затем происходит отбор (с замещением) всех п особей для дальнейшей генетической обработки, согласно величине Ps(i). Простейший пропорциональный отбор — рулетка (roulette-wheel selection) — отбирает особей с помощью n «запусков» рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. Размер i-ro сектора пропорционален соответствующей величине Ps(i). При таком отборе члены популяции с более высо­кой приспособленностью с большей вероятность будут чаще выбираться, чем особи с низкой приспособленностью.

После отбора п выбранных особей подвергаются кроссоверу (иногда называемому рекомбинацией) с заданной вероятностью Рс. n строк случайным образом разбиваются на n/2 пары. Для каждой пары с вероятностью Рс мо­жет применяться кроссовер. Соответственно с вероятностью 1-Рс кроссовер не происходит и неизмененные особи переходят на стадию мутации. Если кроссовер происходит, полученные потомки заменяют собой родителей и переходят к мутации.

Одноточечный кроссовер работает следующим образом. Сначала случайным образом выбирается одна из /-1 точек разрыва. (Точка разрыва — участок между соседними битами в строке.) Обе родительские структуры разрываются на два сегмента по этой точке. Затем, соответствующие сег­менты различных родителей склеиваются и получаются два генотипа по­томков.

Например, предположим, один родитель состоит из 10 нолей, а другой — из 10 единиц. Пусть из 9 возможных точек разрыва выбрана точка 3. Родите­ли и их потомки показаны ниже.

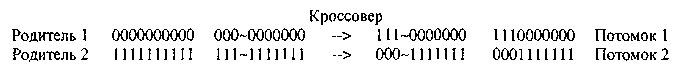
После того как закончится стадия кроссовера, выполняются операторы мутации. В каждой строке, которая подвергается мутации, каждый бит с вероятностью Рm изменяется на противоположный. Популяция, полученная после мутации, записывается поверх предыдущий, и этим цикл одного поколения завершается. Последующие поколения обрабатываются таким же об­разом: отбор, кроссовер и мутация.

В настоящее время исследователи генетических алгоритмов предлагают много других операторов отбора, кроссовера и мутации. Вот лишь наиболее распространенные из них. Прежде всего, турнирный отбор. Турнирный от­бор реализует п турниров, чтобы выбрать п особей. Каждый турнир построен на выборке к элементов из популяции, и выбора лучшей особи среди них. Наиболее распространен турнирный отбор с k - 2.

Элитные методы отбора гарантируют, что при отборе обязательно будут выживать лучший или лучшие члены популяции совокупности. Наиболее распространена процедура обязательного сохранения только одной лучшей особи, если она не прошла, как другие, через процесс отбора, кроссовера и мутации. Элитизм может быть внедрен практически в любой стандартный метод отбора.

Двухточечный кроссовер и равномерный кроссовер — вполне достойные альтернативы одноточечному оператору. В двухточечном кроссовере выбираются две точки разрыва, и родительские хромосомы обмениваются сегментом, который находится между двумя этими точками. В равномерном кроссовере каждый бит первого родителя наследуется первым потомком с заданной вероятностью; в противном случае этот бит передается второму потомку, и наоборот.

Холланд показал, что, как генетический алгоритм явным образом обрабатывает п строк на каждом поколении, в то же время неявно обрабатываются порядка п таких коротких шим низкого порядка и с высокой приспособлен­ностью (полезных шим, «useful schemata»). Он называл это явление «неяв­ным параллелизмом». Для решения реальных задач присутствие неявного параллелизма означает, что большая популяция имеет больше возможностей локализовать решение экспоненциально быстрее популяции с меньшим чис­лом особей. В то время как теорема шим предсказывает рост примеров хороших шим, сама теорема весьма упрощенно описывает поведение генетиче­ского алгоритма. Прежде всего, F_cp(G(H)) и F_cp. не остаются постоянными от поколения к поколению. Приспособленности членов популяции знамена­тельно изменяются уже после нескольких первых поколений. Во-вторых, теорема шим объясняет потери шим, но не появление новых. Новые шимы часто создаются кроссовером и мутацией. Кроме того, по мере эволюции, члены популяции становятся все более и более похожими друг на друга так, что разрушенные шимы будут сразу же восстановлены. Наконец, доказа­тельство теоремы шим построено на элементах теории вероятности, и следо­вательно, не учитывает разброс значений, в многих интересных задачах раз­брос значений приспособленности шимы может быть достаточно велик, делая процесс формирования шим очень сложным. Существенная разница приспособленности шимы может привести к сходимости к неоптимальному решению.

Некоторые исследователи критиковали обычно быструю сходимость генетических алгоритмов, заявляя, что испытание огромных количеств перекрывающихся шим требует большей выборки и более медленной, более управляемой сходимости. В то время как увеличить выборку шим можно увеличив размер популяции, методология управления сходимостью простого генетического алгоритма до сих пор не выработана.

Генетические операторы Холланда могут быть использованы для прогнозирования курсов ценных бумаг на фондовом рынке с использованием при­митивов чартов и посредством методологии обучения синтаксическим образам, описанной выше. Новые правила могут генерироваться посредством систематической модификации значений, применением генетического алгоритма, который отыскивает улучшения, коэффициента оценки для вновь ге­нерируемых цепочек представленных в табл. 11.3. Одновременно выделяют­ся те цепочки, качества которых ниже одной из установленных границ, тем самым эффективно исключается возможность остаться кандидатом на вы­живание в следующем поколении.