X(изолятор(X) не проводит электрический ток(X)).

Выражение во внешних скобках читается следую­щим образом: если х изолятор, то х не проводит элект­рический ток. Стоящий впереди квантор общности обобщает это свойство на все изоляторы.

«Стекло» представляет собой одно из значений переменной X. Обозначим его через a (символ второго типа). «Изолятор» как предикат обозначим через p (сим­вол четвертого типа). Еще одним предикатом является свойство «не проводит электрический ток»; обозна­чим его через q. Тогда первая предпосылка примет вид

,

а вторая предпосылка — вид р(а).

Подставляя значение X=а и последнее выраже­ние в предыдущее, получаем

откуда следует искомое заключение

что означает «стекло не проводит электрический ток»

Исчисление высказываний характеризуется ограниченными возможностями для представления знаний. Объясняется это тем, что в исчислении высказываний рассматриваются логические связи только между утверждениями, а сама структура утверждений не анализируется. Поэтому в исчислении высказываний нельзя установить связь между тем, о чем идет речь (объект) и тем, что сообщается о данном объекте (предикат). Исчисление предикатов рассматривает логические связи между различными элементами утверждений.

Язык исчисления предикатов можно использовать в качестве языка запросов к реляционной базе данных. В этом случае пользователь записывает предложения (запросы) на языке исчисления предикатов. Помимо обычных (реляционных) баз данных имеются дедуктивные базы данных, содержащие интенсиональную и экстенсиональную части и, следовательно, являющиеся комбинацией баз знаний и баз данных. В дедуктивных базах данных для получения фактов из аксиом используются методы доказательства теорем.

Основным достоинством использования исчислений предикатов в качестве моделей представления знаний является наличие единообразной формальной процедуры доказательства теорем. Однако высокая степень единообразия влечет за собой и основной недостаток данного подхода – сложность использования при доказательстве эвристик, отражающих специфику конкретной предметной области. Указанный недостаток является особенно важным при построении экспертных систем, вычислительная мощность которых в основном определяется знаниями, характеризующими специфику проблемной области. К другим недостаткам формальных систем следует отнести их монотонность, отсутствие средств для структурирования используемых элементов и недопустимость противоречий.

Нечеткие множества и нечеткая логика

Традиционная формальная логика основывается на двух предположениях. Первое связано с установлением принадлежности - для любого элемента и множества, принадлежащего некоторому универсуму, элемент является либо членом множества, либо членом дополнения множества. Второе предположение основано на законе исключения третьего, утверждающем, что элемент не может одновременно принадлежать множеству и его дополнению. Оба этих предположения нарушаются в теории нечетких множеств (fuzzy set theory).

Нечеткая логика - надмножество Булевой логики, которая была расширена с целью обработки концепции частичной правды - значения истинности между " полностью истинным " и " полностью ложным ". Она была введена доктором Lotfi Zadeh UC/BERKELEY в 1960-ых как способ моделирования неопределенностей естественного языка.

Главное утверждение Заде заключается в том, что теория вероятностей является хорошим инструментом для измерения случайности информации, но не подходит для измерения смысла информации. По мнению Заде человеческий способ рассуждений, опирающийся на естественный язык, не может быть описан в рамках традиционных математических формализмов. Эти формализмам присуща строгая однозначность интерпретации, а все, что связано с использованием естественного языка, имеет многозначную интерпретацию. С самого начала основная прагматическая цель Заде - создание аппарата, способного моделировать человеческие рассуждения и объяснять человеческие приемы принятия решений в ходе решения различных задач. Идеи Заде и его последователей находят применение при создании систем, понимающих тексты на естественном языке, при создании планирующих систем, опирающихся на неполную информацию, при обработке зрительных сигналов, при управлении техническими, социальными и экономическими системами, в системах искусственного интеллекта и робототехнических системах.

Л.Заде обосновал следующие необходимые характеристики нечеткой логики.

• В нечеткой логике точное рассуждение рассматривается как частный случай приблизительного рассуждения.

• В нечеткой логике все - вопрос степени.

• Любая логическая система может быть фаззифицирована.

• В нечеткой логике, знание интерпретируется как совокупность гибких или, эквивалентно, нечетких ограничений на совокупность переменных.

• Логический вывод рассматривается как процесс распространения гибких ограничений.

Третье утверждение, следовательно, Булева логика - подмножество нечеткой логики.

Классическая теория множеств: пусть имеется множество X и его собственное подмножество A, то есть . Тогда, подмножество A можно представить в виде совокупности упорядоченных пар

где - функция принадлежности. Первый элемент упорядоченной пары - элемент множества A, второй элемент - элемент из множества {0, 1}. Причем

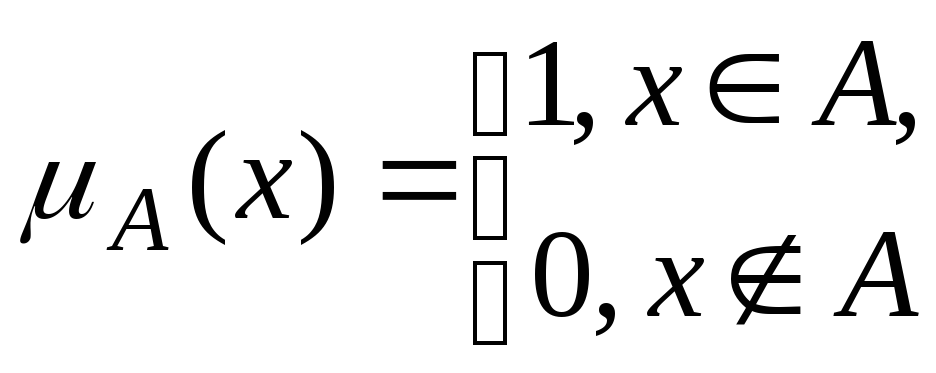
Например, Рис. 1 ниже иллюстрирует дуальное множество, характеризующее температуру в комнате.

Рис.1. Множество, характеризующее температуру в комнате (функция принадлежности для четкого множества)

Наиболее очевидные особенности ограничения традиционной формальной логики, которые могут быть замечены ясно из диаграммы - то, что элементы являются взаимно исключаемыми - не возможно иметь членство больше чем в одном множестве. Однако, мнения относительно того, является ли погода при 0 градусах по Шкале Цельсия " холодной " или " прохладной ", будут широко меняться, следовательно, нам необходимо экспертное знание с помощью которого мы должны определить нашу систему математически в соответствии с человеческим миром. Ясно, что данная математическая модель определит переход из количества типа " теплый " к " горячий " относительно теплоты по Шкале Цельсия скачкообразно. В реальном мире переход от теплого к горячему произошел бы плавно.

Определение нечеткого подмножества получается как обобщение четкого подмножества. Нечетким подмножеством A множества X называется совокупность упорядоченных пар

где функция принадлежности каждому элементу x ставит в соответствие действительное число из интервала [1,0], указывающее степень принадлежности элемента x подмножеству A. Значение нуль используется для представления полной не принадлежности, значение один используется для представления полной принадлежности, и значения между ними используется для представления промежуточных значений СТЕПЕНИ ПРИНАДЛЕЖНОСТИ. Часто в выражении вместо запятой, отделяющей x от , используется вертикальная черта, то есть . Таким образом, имея понятие нечеткого подмножества, можно представить объекты (сущности) предметной области, характеризуемые размытыми границами описаний.

Рис. 2 показывает, как нечеткие множества, определяющие количество той же самой информации могут описывать естественный переход от теплого к горячему.

Рис.2. Нечеткое множество, характеризующее температуру в комнате

При практическом применении нечетких множеств важными являются понятия нечеткой и лингвистической переменной. Нечеткая переменная определяется набором , где - название нечеткой переменной; - область ее определения; - нечеткое подмножество множества , включающее те возможные значения , которые обусловлены названием . Лингвистической называют переменную, значениями которой являются слова и фразы естественного языка (термы). Формально лингвистическая переменная определяется набором

,

где - название переменной; T - терм-множество переменной , то есть множество ее значений, причем каждое из таких значений (терм) есть название нечеткой переменной , областью определения которой является множество X; G - синтаксическая процедура, порождающая на множестве T значения переменной ; M - семантическая процедура, которая отображает каждое новое значение нечеткой переменной в нечеткое подмножество множества X.

Рассмотрим пример. Пусть определяется рост человека с помощью понятий-значений: "низкий", "средний", "высокий". При этом, минимальный и максимальный рост соответственно равны 95 см и 195 см. Формально, лингвистическая переменная "рост" представляется набором

<РОСТ, {НИЗКИЙ, СРЕДНИЙ, ВЫСОКИЙ}, [95,195],G,M>,

где G - процедура перебора элементов терм-множества T; M - процедура, которая ставит в соответствие нечетким переменным ("низкий", "средний", "высокий") соответствующие величины. Иными словами, процедура M определяет взаимосвязь нечетких переменных с соответствующими функциями принадлежности.

На графике это выглядит так:

Согласно данному определению, мы имеем следующие значения

Персона	Рост	Низкий	Средний	Высокий
1	95	1	0	0
2	163	0.4	0.2	0
3	170	0	0.7	0
4	175	0	1	0
5	180	0	0,5	0.3
6	187	0	0	0.7
7	195	0	0	1

В зависимости от характера множества X лингвистические переменные подразделяются на числовые и нечисловые. Числовой называется такая лингвистическая переменная, для которой базовая переменная определена на числовом множестве. В рассматриваемом примере лингвистическая переменная "РОСТ" является числовой, а ее значения (нечеткие переменные) - нечеткими числами. Каждой нечеткой переменной на рисунке 3 условно соответствует трапецеидальная функция принадлежности, которая определяет степень принадлежности того или иного роста человека к соответствующему нечеткому понятию. Так, согласно рисунку, нечеткую переменную "средний" можно определить с помощью следующего нечеткого множества

"средний"=

Здесь наивысшую степень принадлежности подмножеству "средний" имеет рост 175 см. Росты 163, 170 см и 180 см принадлежат подмножеству "средний" в меньшей степени. Росты 187 см и 195 см подмножеству не принадлежат.

Нечеткие и лингвистические переменные позволяют формулировать нечеткие утверждения, например "Сегодня не холодно" или "Если тепло и влажно, овощи растут быстро". Подобные утверждения являются объектом исследования нечеткой логики. Важно отметить, что в отличие от формальной логики, которая использует таблицы истинности, нечеткая логика опирается на операции, выполняемые над нечеткими множествами. Рассмотрим основные из них.

Будем рассматривать нечеткие подмножества A и B множества X.

Нечеткие множества A и B равны (A = B), если

Множество B содержится во множестве A, если

Множества A и B дополняют друг друга, если

Множество с функцией принадлежности есть дополнение к множеству A.

Пересечение двух нечетких множеств A и B () - это нечеткое множество, функция принадлежности которого определяется выражением

Объединением нечетких множеств A и B () называется нечеткое множество с функцией принадлежности

,

Алгебраическая сумма нечетких множеств A и B () есть нечеткое множество с функцией принадлежности

Дизъюнктивная сумма нечетких множеств A и B определяется через операции объединения и пересечения

Важным понятием теории нечетких множеств является нечеткое отношение. Нечетким бинарным отношением называется подмножество декартового произведения двух множеств и

где - функция принадлежности пары элементов к P.

Пусть множества и состоят из элементов , . Тогда, нечеткое бинарное отношение можно задать матрицей, элементами которой будут значения :

В частности, данная матрица может представлять нечеткое отношение " примерно равно ".

Часто нечеткие отношения используют для представления правил типа "если A, то B, где A и B нечеткие подмножества (, ). Такое правило обозначается как . Один из способов задания нечеткого отношения, соответствующего правилу , состоит в использовании формулы декартового произведения множеств A и B ():

здесь

причем .

Пример. Пусть . Определим нечеткое множество A, соответствующее малым числам, и нечеткое множество B, соответствующее большим числам:

Тогда правилу "если малое, то большое" будет соответствовать нечеткое отношение:

1 2 3 4

В некоторых случаях полезной может оказаться операция "компенсирующее И", объединяющая в себе свойства конъюнкции и дизъюнкции. Функция принадлежности для этой операции задается следующей формулой

,

где - параметр, заданный на интервале [0,1]. При малых значениях "компенсирующее И" соответствует конъюнкции, при значениях близких к единице - дизъюнкции.