18. Определение мощности насосов для перекачки нефти
Применительно к насосам различают несколько видов мощности:
- полезная мощность:
Nпол= ; (1)
- мощность, потребляемая насосом:
; (2)
- мощность насосно-силового агрегата:
NНСА= , (3)
где ηдв – КПД двигателя; ηпер – КПД механической передачи между двигателем и насосом.
Технологический расчет магистральных трубопроводов при стационарном режиме перекачки
19. Закон Паскаля
Распределение давления в покоящейся жидкости находится из уравнений равновесия Эйлера:
или
(1)
,
в которых вектор
с компонентами (X, Y, Z) называется плотностью
массовых сил или напряжением массовых
сил (массовая сила, рассчитанная на
единицу массы; размерность — ускорение).
Дифференциальное уравнение поверхности
равного давления (изобарической
поверхности) имеет вид
.
(2)
Поверхность раздела между жидкой и газообразной средой называется свободной поверхностью.
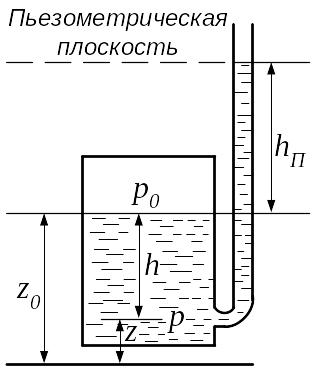
Рис. 1. Закрытый сосуд с покоящейся жидкостью (справа показана вертикальная открытая трубка — пьезометр)
В однородной несжимаемой жидкости (ρ = const), находящейся в равновесии под действием силы тяжести (X=0, Y=0, Z= — g , осъ z направлена вверх), распределение давления определяется из выражения
(3)
где р0 — давление в точках горизонтальной плоскости с координатой z0 (в качестве такой плоскости чаще всего выбирается свободная поверхность жидкости); z — координата точки, в которой определяется давление р; h = z0 — z — глубина погружения рассматриваемой точки по отношению к плоскости с координатой z0 ; g — ускорение свободного падения (рис. 1).
Формула (3) носит название основного уравнения гидростатики. Из нее следует закон Паскаля: изменение давления в какой-либо покоящейся и продолжающей оставаться в покое точке жидкости передается одинаковым образом всем точкам этой жидкости.
20. Уравнение Дарси-Вейсбаха
Запас механической энергии жидкости, которым обладает каждая ее единица силы тяжести, называется напором Н. Из-за работы сил трения напор по ходу движения жидкости непрерывно уменьшается. Разность начального и конечного напоров между двумя какими-либо живыми сечениями потока называется потерями напора hпот . Эти потери напора представляют собой сумму потерь напора на трение по длине потока hд и в местных сопротивлениях hм
Hпот =hд+hм. (1)
Потери напора по длине для труб постоянного диаметра определяются по формуле Дарси-Вейсбаха
(2)
где — коэффициент гидравлического сопротивления (гидравлического трения); l — длина трубы; d — ее внутренний диаметр; — средняя скорость потока.
В общем случае является функцией числа Рейнольдса (Re) и относительной шероховатости стенок трубы /d. Здесь — абсолютная эквивалентная шероховатость, т.е. такая высота равномерно-зернистой шероховатости, при которой в квадратичной зоне сопротивления потери напора равны потерям напора для данной естественной шероховатости трубы (примерные значения — приведены в прил. 1).
Итак, в общем виде = (Re, /d). Численно определяется в зависимости от области сопротивления. При ламинарном режиме движения (Re < Reкр ), = (Re)
=64/Re. (3)
В этом случае выражение (5.2) принимает вид формулы Пуазейля
(4)
При турбулентном режиме движения (Re > Reкр) различают три зоны сопротивления.
1. Зона гидравлически гладких труб (Reкp
< Re 10
;
=
(Re)):
= 0,3164/Re0,25 — (5)
формула Блазиуса, используемая при Re 105 ;
–
формула Конакова, используемая при Re < 3 • 106.
2. Зона шероховатых труб (10d/ < Re 500d/; = (Re, /d):
–
(6)
формула Альтшуля.
3. Зона вполне шероховатых труб или квадратичная зона (Re>500d/; = (/d)):
=0,11 (/d)0,25 – (7)
формула Шифринсона.
С незначительной погрешностью формула Альтшуля может использоваться как универсальная для всей турбулентной области течения. Если живое сечение не имеет формы круга, то формулы (2), (5), (6) и (7) могут использоваться при турбулентном движении с заменой диаметра трубы d на учетверенный гидравлический радиус R. При ламинарном движении в этом случае используются специальные формулы, приводимые в справочниках.