- •270200 – Транспортное строительство
- •Введение
- •1. Классификация и составные элементы грунтов
- •Классификация грунтов по гранулометрическому составу
- •2. Вода в грунте
- •Коэффициент водоотдачи грунтов
- •3. Газы в грунте
- •4. Структурные связи и строение грунтов
- •5. Физические свойства грунтов
- •Классификация глинистых грунтов по числу пластичности
- •Классификация глинистых грунтов по индексу текучести
- •6. Основные закономерности механики грунтов
- •7. Общий случай компрессионной зависимости
- •8. Водопроницаемость грунтов. Закон ламинарной фильтрации
- •Значения коэффициента фильтрации песков
- •9. Эффективные и нейтральные давления грунтовой массы
- •10. Контактное сопротивление грунтов сдвигу
- •11. Сопротивление сдвигу при сложном напряженном состоянии. Теория прочности кулона – мора
- •12. Деформируемость грунтов
- •13. Предельное напряженное состояние грунтов
- •Фазы напряженного состояния грунта
- •14. Критические нагрузки на грунт
- •15. Определение напряжений в грунтовом массиве
- •16. Распределение напряжений от собственного веса грунта
- •17. Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности
- •18. Расчет осадок фундаментов
- •19. Расчет устойчивости откосов
- •20. Определение давления грунтов на ограждения
- •21. Особые грунты
- •Практические задания
- •Задание №1
- •Данные, принимаемые по последней цифре шифра
- •Данные, принимаемые по предпоследней цифре шифра
- •Данные, принимаемые по второй цифре шифра
- •Данные, принимаемые по первой цифре шифра
- •Сводная таблица нормативных характеристик грунтов (пример)
- •Задание №2
- •Значение коэффициента бокового давления
- •Пример расчета
- •Содержание работы
- •Порядок выполнения работы
- •Пример расчета
- •Задание №4
- •Исходные данные для расчета
- •Значение углов и для определения центра вращения
- •Пример расчета
- •Расчет устойчивости откоса
- •Задание № 5
- •Определение активного давления на подпорную стенку без нагрузки на поверхности засыпки для однородного грунта
- •Определение активного давления на подпорную стенку с учетом равномерно распределенной нагрузки на поверхности засыпки для однородного грунта
- •Определение активного давления на подпорную стенку с учетом равномерно распределенной нагрузки на поверхности засыпки для неоднородных грунтов
- •Пример расчета
- •Порядок выполнения работы
- •Исходные данные для расчета подпорной стенки
- •Задание №6
- •Пример расчета.
- •Компрессионные испытания
- •II слой – супесь твердая (глубина отбора 2,8 м)
- •V слой – суглинок полутвердый (глубина отбора 7 м)
- •Штамповые испытания
- •Расчет осадки элементарных грунтовых слоев
- •Тестовый контроль знаний
- •Вопросы к зачету
- •Нормативные значения модуля деформации пылевато-глинистых нелёссовых грунтов
- •Нормативные значения характеристик с, кПа, и φ, град, для пылевато-глинистых нелёссовых грунтов четвертичных отложений
- •Классификация природных дисперсных грунтов
- •Классификация крупнообломочных грунтов и песков по гранулометрическому составу
- •Классификация крупнообломочных грунтов и песков по коэффициенту водонасыщения
- •Классификация песков по коэффициенту пористости
- •Классификация глинистых грунтов по числу пластичности
- •Классификация глинистых грунтов по гранулометрическому составу и числу пластичности
- •Классификация глинистых грунтов по наличию включений
- •Классификация глинистых грунтов по показателю текучести
- •Расчетные сопротивления грунтов
- •Расчетные сопротивления r0 песчаных грунтов
- •Расчетные сопротивления r0 пылевато-глинистых (непросадочных) грунтов
- •Связь между наиболее употребляемыми в механике грунтов единицами измерения в системе си и технической системе
- •Библиографический список Нормативная
- •Основная
- •Оглавление
- •308012, Г. Белгород, ул. Костюкова,46
Содержание работы
Давление на основание, передаваемое по подошве фундамента, распространяется в грунте во все стороны, постепенно уменьшаясь. Рассмотрим случай, когда фундамент передает на основание давление от равномерной силы Р (кПа), центр тяжести которого N проходит через центр подошвы (рис. 31).
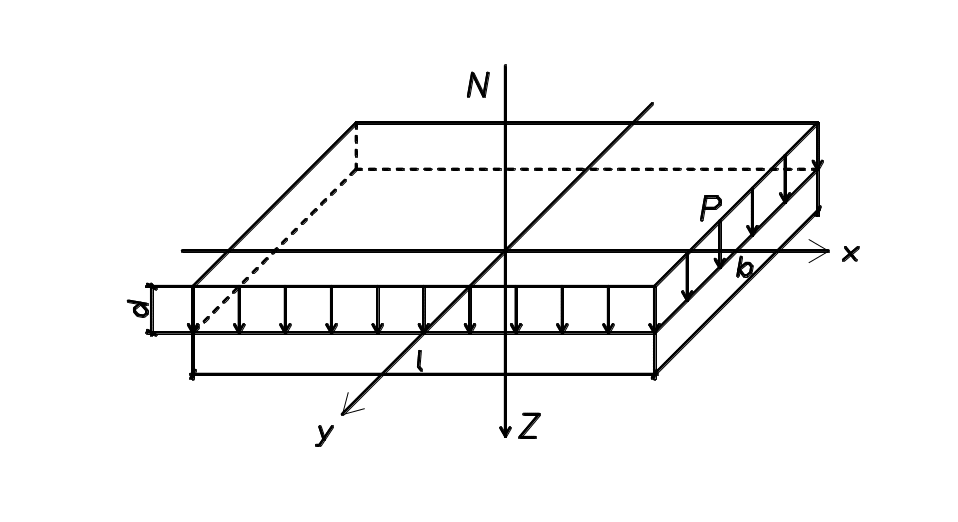
Рис. 31. Схема действия сил от равномерной нагрузки
Наибольшие нормальные напряжения (zp) возникают по вертикальной оси Z, проходящей по центру подошвы фундамента. По мере увеличения глубины они постепенно уменьшаются по величине.
Расчет напряжений производится по формуле
![]() ,
,
где – коэффициент рассеивания;
Р0 – осадочное давление на подошве, кПа, равное
![]() ,
,
где – удельный вес грунта выше подошвы, кН/м3;
d – глубина заложения фундамента, м.
Значения принимаются по таблице СНиП 2.02.01-83 (см. приложение В) в зависимости от соотношений =2z/b и =l/b, где z – глубина определения напряжения, b и l – ширина и длина подошвы фундамента. Для промежуточных значений и коэффициент определяют интерполяцией.
Напряжение под угловыми точками фундамента вычисляется по формуле
![]() ,
,
при этом соотношение принимается равным =z/b.
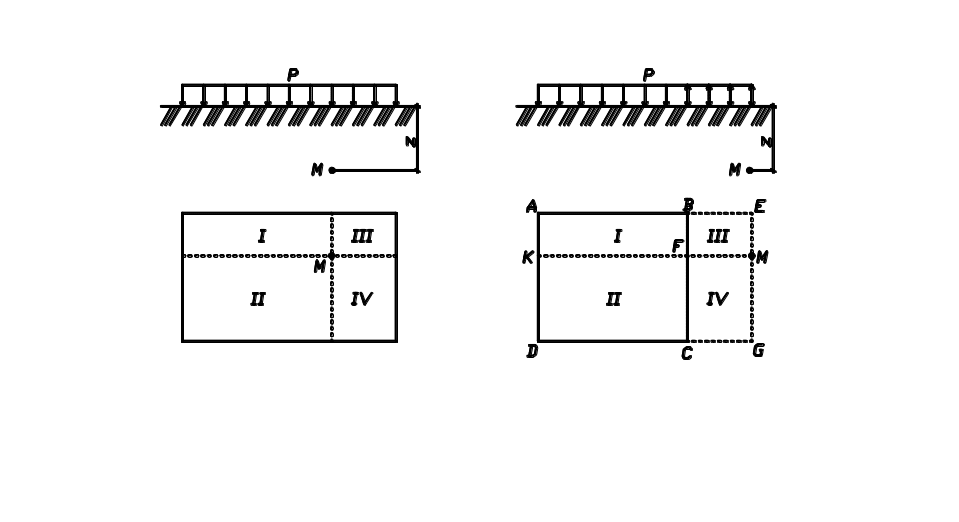
Для определения вертикальных напряжений в любой точке основания, в том числе за проекцией площади нагружения, применяется метод угловых точек. Если напряжения определяют в точке, находящейся под загруженной областью (рис. 32, а), то загруженную площадь разбивают на четыре прямоугольника I, II, III и IV, для каждого из которых точка М является угловой, и напряжения находят как сумму давлений под угловыми точками четырех площадей загружения:
![]()
|
а) |
б) |
|
||
Рис. 32. Схема определения напряжений от равномерно распределенной нагрузки методом угловых точек, находящихся:
а – в пределах загруженной площади; б – вне пределов загруженной площади
Если же точка М находится вне пределов площади загружения ABCD (рис. 32, б), она считается угловой для четырех фиктивных площадей загружения I, II, III и IV (прямоугольники AEMK, KMGD, BEMF, FMGC). При этом в пределах площадей I и II направление нагрузки совпадает с направлением исходной нагрузки, а в пределах площадей III и IV направление фиктивной нагрузки является обратным направлению исходной нагрузки и напряжения находят по выражению:
![]()
Порядок выполнения работы
Студенты получают индивидуальные задания, состоящие из размеров фундамента (b, l, d), величины давления на подошве (Р). Необходимо определить напряжения вдоль оси Х в точках А, В, С, В′, C′ на различной глубине z1, z2, z3, z4 и построить эпюры сжимающих напряжений по вертикальным и горизонтальным сечениям массива. Значение удельного веса () назначается преподавателем.
Пример расчета
Исходные данные: Р = 300 кПа, b = 2,0 м, l = 3,0 м, d = 1,8 м. Необходимо определить:
напряжения в точках А, В, С, В′, C′ (рис. 33), расположенных на глубине z1 = 1,0 м, z2 = 2,0 м, z3 = 3,0 м, z4 = 4,0 м от подошвы фундамента и построить эпюры сжимающих напряжений по вертикальным и горизонтальным сечениям;
напряжения в точке М по заданным координатам xМ = 3 м, yМ = 2 м от центра фундамента, zМ = 2,5 м.
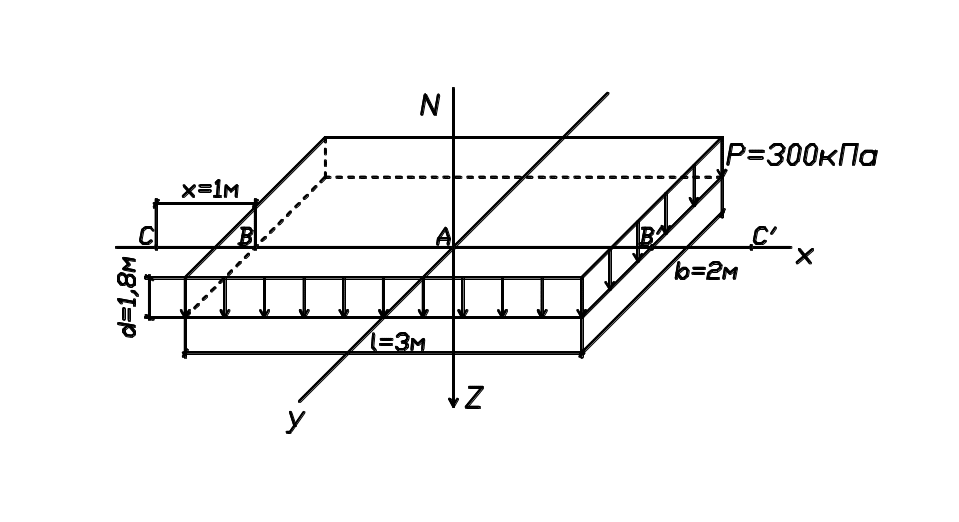
Рис. 33. Схема определения напряжений от равномерно распределенной нагрузки
Последовательность расчета
1. Определим осадочное давление на подошве, принимая значение удельного веса грунта = 16,0 кН/м3: Р0 = P - d = 300 - 16,0·1,8 = 271,2 кПа.
2. Найдем вертикальные напряжения на подошве фундамента в точках А, В (В′), С (С′): Значения коэффициента принимаем по табл. В.1 приложения В, исходя из величин и .
а) точка А: = 2z/b = 2·0/2,0 =0 и = l/b =3,0/2,0 = 1,5. Получим = 1.
![]() =
1·271,2 = 271,2 кПа;
=
1·271,2 = 271,2 кПа;
б) точка В (В′): загруженную площадь разбиваем на два прямоугольника I и II для каждого из которых точка В (В′) является угловой, и напряжения находим как сумму давлений под угловыми точками двух площадей загружения.
1 = 2= z/b = 0/1,0 = 0 и 1 = 2= l/b = 3,0/1,0 = 3. Получим = 1.
![]() 0
= 0,25·(1+1)·271,2 = 135,6 кПа;
0
= 0,25·(1+1)·271,2 = 135,6 кПа;
в) точка С (С′) находится вне пределов площади загружения (рис. 33), она считается угловой для четырех фиктивных площадей загружения I, II, III и IV.
1 = 2 = z/b = 0/1,0 = 0 и 1 = 2= l/b = 4,0/1,0 = 4. Получим = 1.
3 = 4= z/b = 0/1,0 = 0 и 3 = 4= l/b = 1,0/1,0 =1. Получим = 1.
![]() =
0,25·(1 + 1 – 1 - 1)·271,2 = 0 кПа.
=
0,25·(1 + 1 – 1 - 1)·271,2 = 0 кПа.
3. Найдем вертикальные напряжения на глубине z = 1,0 м.
а) точка А: = 2z/b = 2·1,0/2,0 = 1,0 и = l/b = 3,0/2,0 = 1,5. После интерполяции получим = 0,771.
= 0,771·271,2 = 209,6 кПа.
б) точка В (В′): загруженную площадь разбиваем на два прямоугольника I и II для каждого из которых точка В (В′) является угловой, и напряжения находим как сумму давлений под угловыми точками двух площадей загружения.
1 = 2= z/b = 1/1,0 = 0 и 1 = 2=l/b = 3,0/1,0 = 3. Получим = 0,81.
![]() =
0,25· (0,81+0,81) ·271,2 = 109,84 кПа;
=
0,25· (0,81+0,81) ·271,2 = 109,84 кПа;
в) точка С (С′) находится вне пределов площади загружения (рис. 33), она считается угловой для четырех фиктивных площадей загружения I, II, III и IV
1 = 2= z/b = 1/1,0 = 0 и 1 = 2 = l/b =4,0/1,0 = 4. Получим = 0,816.
3 = 4= z/b =1/1,0 = 0 и 3 = 4 = l/b = 1,0/1,0 = 1. Получим = 0,703.
=0,25· (0,816 + 0,816 - 0,703 - 0,703) ·271,2 = 15,26 кПа.
Аналогичным образом рассчитаем напряжения на глубинах 2, 3 и 4 м.
4. z2 = 2 м.
а) точка А:
= 2z/b = 2·2,0/2,0 = 2,0 и = l/b = 3,0/2,0 = 1,5. После интерполяции получим = 0,426.
= 0,426·271,2 = 115,6 кПа.
б) точка В (В′):
1 = 2= z/b = 2/1,0 = 2 и 1 = 2 = l/b = 3,0/1,0 = 3. Получим = 0,524.
= 0,25·(0,524+0,524)·271,2 = 71,05 кПа;
в) точка С (С′):
1 = 2 = z/b = 2/1,0 = 0 и 1 = 2 = l/b = 4,0/1,0 = 4. Получим = 0,537.
3 = 4 = z/b = 2/1,0 = 0 и 3 = 4 = l/b = 1,0/1,0 = 1. Получим = 0,366.
=0,25· (0,537 + 0,537 - 0,366 - 0,366)·271,2 = 23,19 кПа.
5. z3 = 3 м.
а) точка А:
= 2z/b = 3·2,0/2,0 = 3,0 и = l/b = 3,0/2,0 = 1,5. После интерполяции получим = 0,246.
= 0,246·271,2 = 66,61 кПа.
б) точка В (В′):
1 = 2 = z/b = 3/1,0 = 3 и 1 = 2 = l/b = 3,0/1,0 = 3. Получим = 0,347.
= 0,25·(0,347 + 0,347)·271,2 = 47,05 кПа;
в) точка С (С′):
1 = 2 = z/b = 3/1,0 = 0 и 1 = 2 = l/b = 4,0/1,0 = 4. Получим = 0,369.
3 = 4= z/b = 3/1,0 = 0 и 3 = 4 = l/b = 1,0/1,0 = 1. Получим = 0,18.
=0,25· (0,369 + 0,369 - 0,18 - 0,18)·271,2 = 25,63 кПа.
6. z3 = 4 м.
а) точка А:
= 2z/b = 4·2,0/2,0 = 4,0 и = l/b = 3,0/2,0 = 1,5. После интерполяции получим = 0,153.
= 0,153·271,2 = 41,49 кПа.
б) точка В (В′):
1 = 2= z/b = 4/1,0 = 3 и 1=2= l/b = 3,0/1,0 = 3. Получим = 0,24.
![]() =
0,25·(0,24 + 0,24)·271,2 = 32,61 кПа;
=
0,25·(0,24 + 0,24)·271,2 = 32,61 кПа;
в) точка С (С′):
1 = 2 = z/b= 4/1,0 = 0 и 1 = 2 = l/b = 4,0/1,0 = 4. Получим = 0,264.
3 = 4= z/b = 4/1,0 =0 и 3 = 4= l/b = 1,0/1,0 = 1. Получим = 0,108.
=0,25· (0,264 + 0,264 - 0,108 - 0,108) ·271,2 = 21,15 кПа.
7. Строим эпюры сжимающих напряжений по вертикальным и горизонтальным сечениям (рис. 34):
а) б)
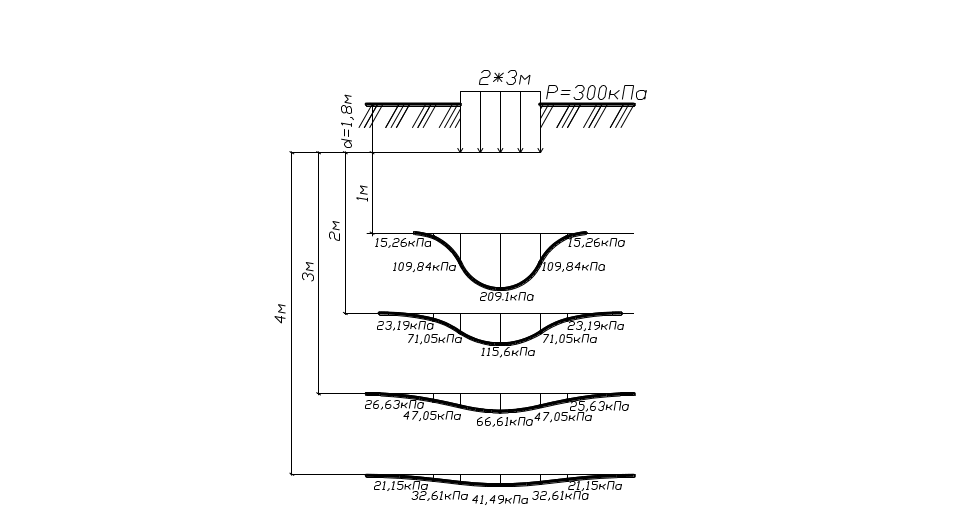
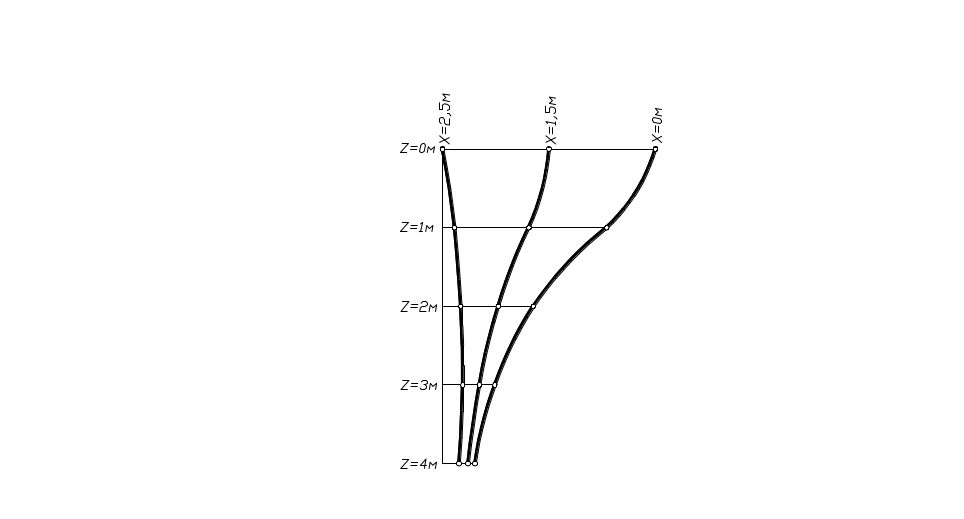
Рис. 34. Эпюры распределения сжимающих напряжений:
а – по вертикальному сечению массива грунта;
б – по горизонтальному сечению массива грунта
8. Определим напряжения в точке М.
Точка М находится вне пределов площади загружения EFJK (рис. 35). Она считается угловой для четырех фиктивных площадей загружения I, II, III, IV (соответственно прямоугольники ELMO, JQMN, FLMN, KQMO). При этом в пределах площадей I и II направление нагрузки совпадает с направлением исходной нагрузки, а в пределах площадей III и IV направление фиктивной нагрузки является обратным направлению исходной нагрузки.
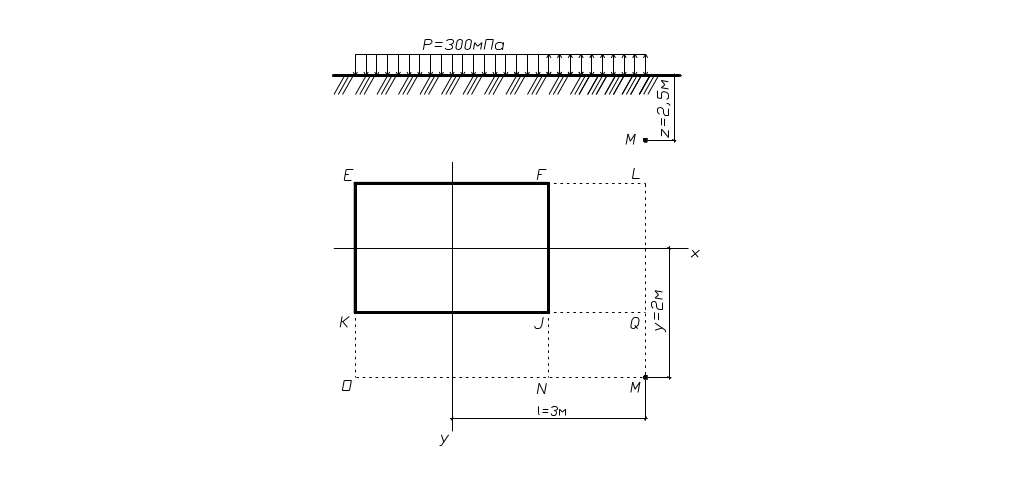
Рис. 35. Схема определения напряжений от равномерно
распределенной нагрузки в точке М
1 = z/b= 2,5/3,0 = 0,833 и 1 = l/b = 4,5/3,0 = 1,5. Получим = 0,840.
2 = z/b = 2,5/1,0 = 2,5 и 2 = l/b = 1,5/1,0 = 1,5. Получим = 0,319.
3 = z/b = 2,5/1,5 = 1,667 и 3 = l/b = 3,0/1,5 = 2. Получим = 0,574.
4 = z/b = 2,5/1,0 = 2,5 и 4 = l/b = 4,5/1,0 = 4,5. Получим = 0,451.
= 0,25· (0,840 + 0,319 - 0,574 - 0,451) ·271,2 = 18,17 кПа.