Методические указания по рядам / с8-16
.doc
б)
;
,
в)
;
.
-
Найти первые четыре отличных от нуля члена разложения в ряд решения дифференциального уравнения, удовлетворяющего начальным условиям.
;
; 
.
-
Разложить функцию
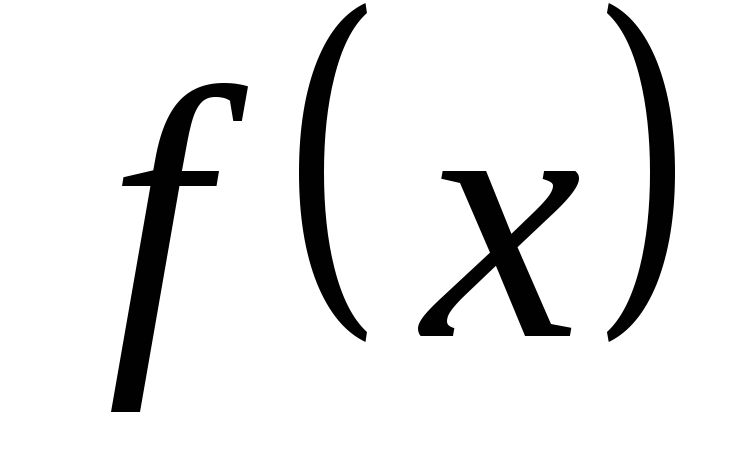в ряд Фурье в интервале
:
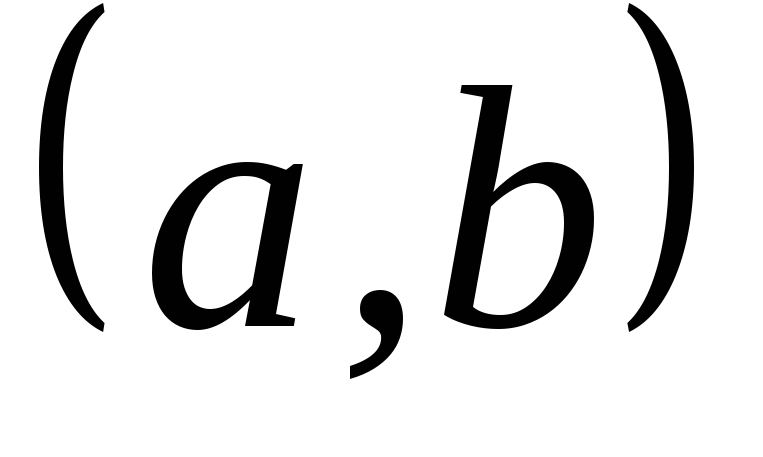а)
;
;
;
,
б)
;
;
по синусам кратных дуг,
в)
;
;
.
-
Вычислить определенный интеграл с точностью
:
.
-
Доказать равномерную сходимость на указанном отрезке:
;
.
ВАРИАНТ 8
-
Проверить, выполняется ли необходимый признак сходимости и сделать соответствующий вывод.
а)
, б)
.
-
Найти сумму ряда:
а)
, б)
.
-
Исследовать сходимость рядов:
а)
, б)
,
в)
, г)
.
-
Найти область сходимости ряда:
а)
, б)
,
в)
.
-
Разложить функцию в ряд Тейлора по степеням
:
а)
;
,
б)
;
,
в)
;
.
-
Найти первые четыре отличных от нуля члена разложения в ряд решения дифференциального уравнения, удовлетворяющего начальным условиям.
;
; 
.
-
Разложить функцию
в ряд Фурье в интервале
:
а)
;
;
;
,
б)
;
;
по синусам кратных дуг,
в)
;
,
.
-
Вычислить определенный интеграл с точностью
:
.
-
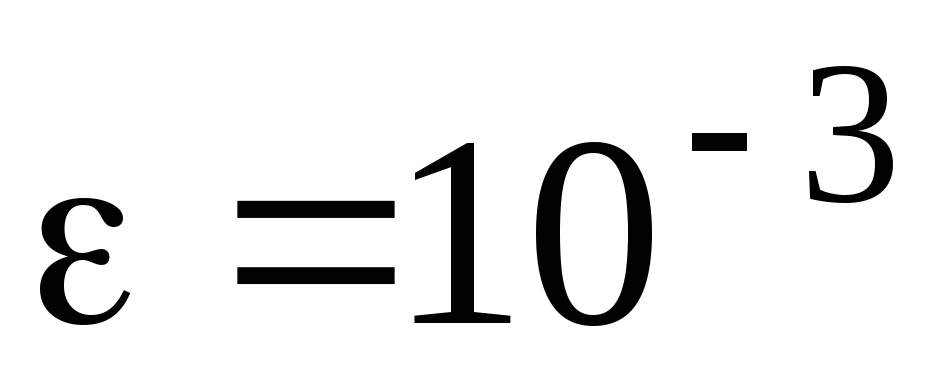Доказать равномерную сходимость на указанном отрезке:
;
.
ВАРИАНТ 9
-
Проверить, выполняется ли необходимый признак сходимости и сделать соответствующий вывод.
а)
, б)
.
-
Найти сумму ряда:
а)
, б)
.
-
Исследовать сходимость рядов:
а)
, б)
,
в)
, г)
.
-
Найти область сходимости ряда:
а)
, б)
,
в)
.
-
Разложить функцию в ряд Тейлора по степеням
:
а)
;
,
б)
;
,
в)
;
.
-
Найти первые четыре отличных от нуля члена разложения в ряд решения дифференциального уравнения, удовлетворяющего начальным условиям.
;
; 
.
-
Разложить функцию
в ряд Фурье в интервале
:
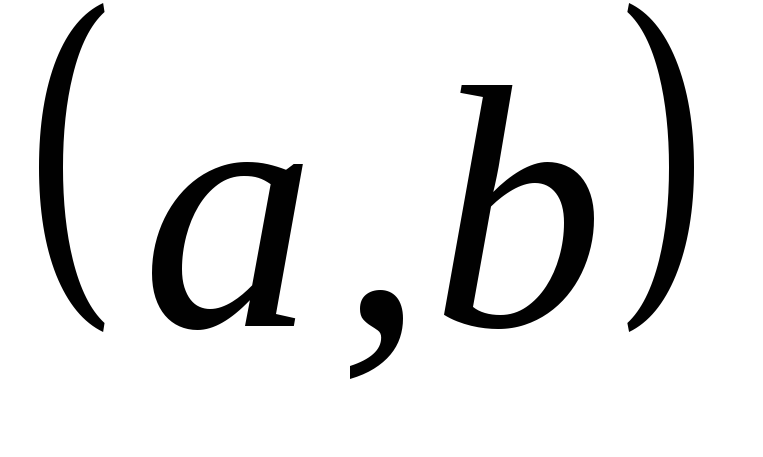а)
;
;
;
,
б)
,
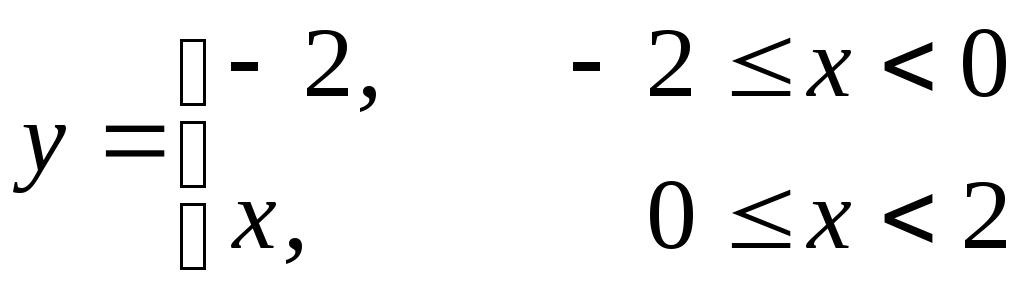в)
;
;
по синусам кратных дуг.
-
Вычислить определенный интеграл с точностью
:
.
-
Доказать равномерную сходимость на указанном отрезке:
;
.
ВАРИАНТ 10
-
Проверить, выполняется ли необходимый признак сходимости и сделать соответствующий вывод.
а)
, б)
.
-
Найти сумму ряда:
а)
, б)
.
-
Исследовать сходимость рядов:
а)
, б)
,
в)
, г)
.
-
Найти область сходимости ряда:
а)
, б)
,
б)
.
-
Разложить функцию в ряд Тейлора по степеням
:
а)
;
,
б)
;
,
в)
;
.
-
Найти первые четыре отличных от нуля члена разложения в ряд решения дифференциального уравнения, удовлетворяющего начальным условиям.
;
; 
.
-
Разложить функцию
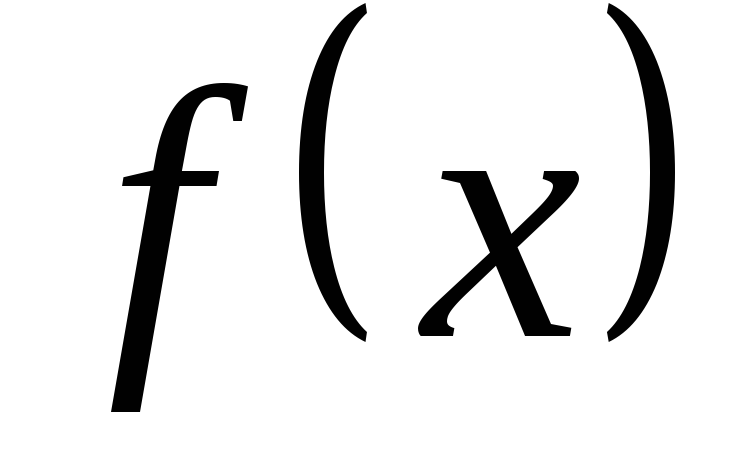в ряд Фурье в интервале
:
а)
;
;
;
,
б)
;
;
по синусам кратных дуг,
в)
;
.
-
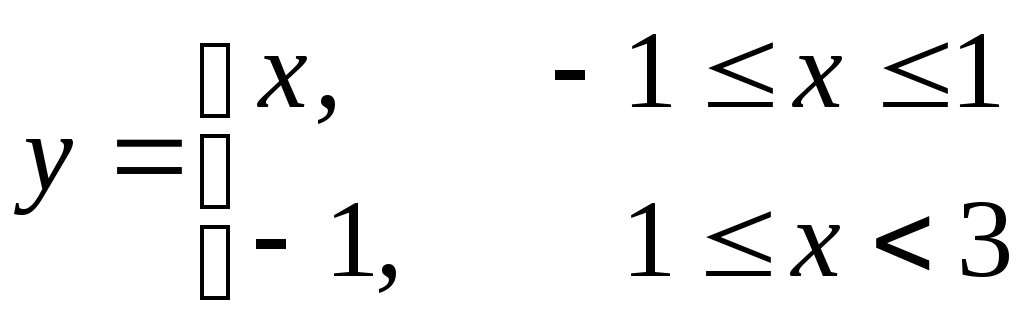Вычислить определенный интеграл с точностью
:
.
-
Доказать равномерную сходимость на указанном отрезке:
;
.
ВАРИАНТ 11
-
Проверить, выполняется ли необходимый признак сходимости и сделать соответствующий вывод.
а)
, б)
.
-
Найти сумму ряда:
а)
, б)
.
-
Исследовать сходимость рядов:
а)
, б)
,
в)
, г)
.
-
Найти область сходимости ряда:
а)
, б)
,
в)
.
-
Разложить функцию в ряд Тейлора по степеням
:
а)
;
,
б)
;
,
в)
;
.
-
Найти первые четыре отличных от нуля члена разложения в ряд решения дифференциального уравнения, удовлетворяющего начальным условиям.
;
; 
.
-
Разложить функцию
в ряд Фурье в интервале
:
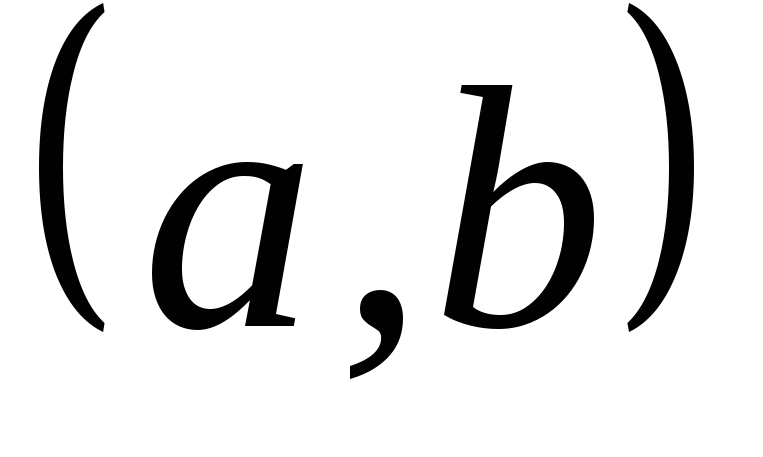а)
;
;
;
,
б)
,
в)
;
;
по синусам кратных дуг.
-
Вычислить определенный интеграл с точностью
:
.
-
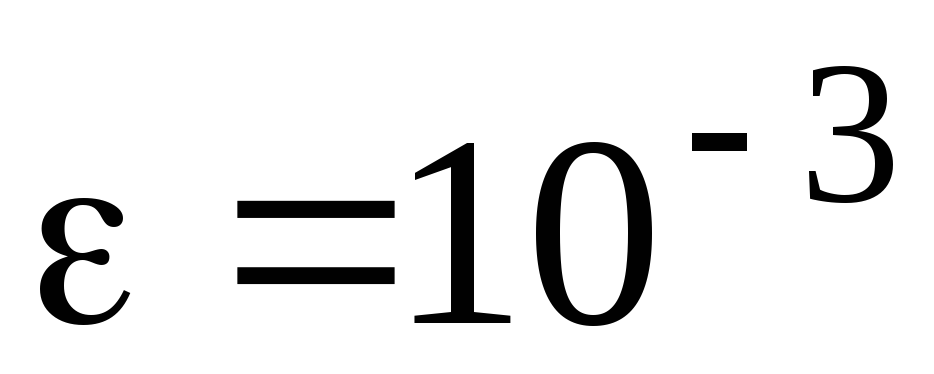Доказать равномерную сходимость на указанном отрезке:
;
.
ВАРИАНТ 12
-
Проверить, выполняется ли необходимый признак сходимости и сделать соответствующий вывод.
а)
, б)
.
-
Найти сумму ряда:
а)
, б)
.
-
Исследовать сходимость рядов:
а)
, б)
,
в)
, г)
.
-
Найти область сходимости ряда:
а)
, б)
,
в)
.
-
Разложить функцию в ряд Тейлора по степеням
:
а)
;
,
б)
;
,
в)
;
.
-
Найти первые четыре отличных от нуля члена разложения в ряд решения дифференциального уравнения, удовлетворяющего начальным условиям.
;
; 
.
-
Разложить функцию
в ряд Фурье в интервале
:
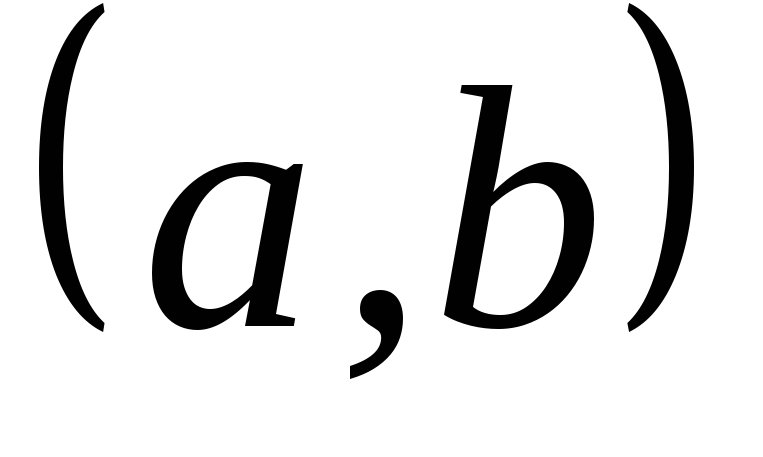а)
;
;
;
,
б)
,
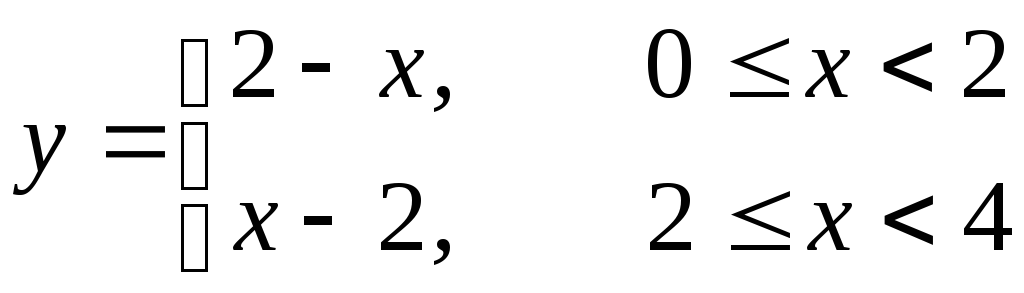в)
;
;
по синусам кратных дуг.
-
Вычислить определенный интеграл с точностью
:
.
-
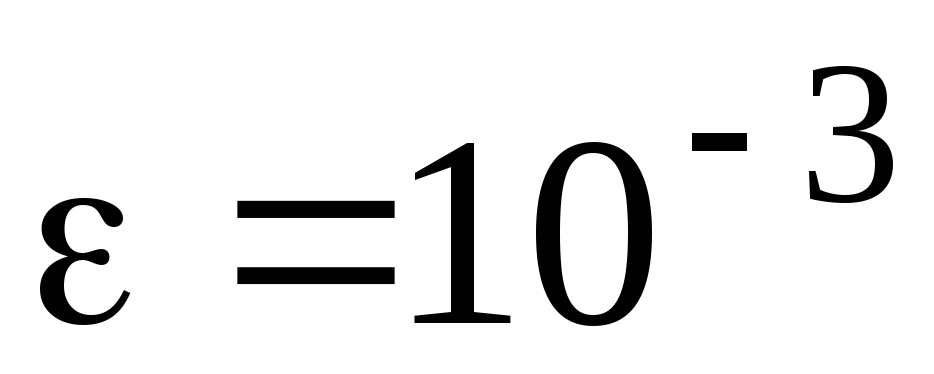Доказать равномерную сходимость на указанном отрезке:
;
.
ВАРИАНТ 13
-
Проверить, выполняется ли необходимый признак сходимости и сделать соответствующий вывод.
а)
, б)
.
-
Найти сумму ряда:
а)
, б)
.
-
Исследовать сходимость рядов:
а)
, б)
,
в)
, г)
.
-
Найти область сходимости ряда:
а)
, б)
,
в)
.
-
Разложить функцию в ряд Тейлора по степеням
:
а)
;
,
б)
;
,
в)
;
.
-
Найти первые четыре отличных от нуля члена разложения в ряд решения дифференциального уравнения, удовлетворяющего начальным условиям.
;
; 
.
-
Разложить функцию
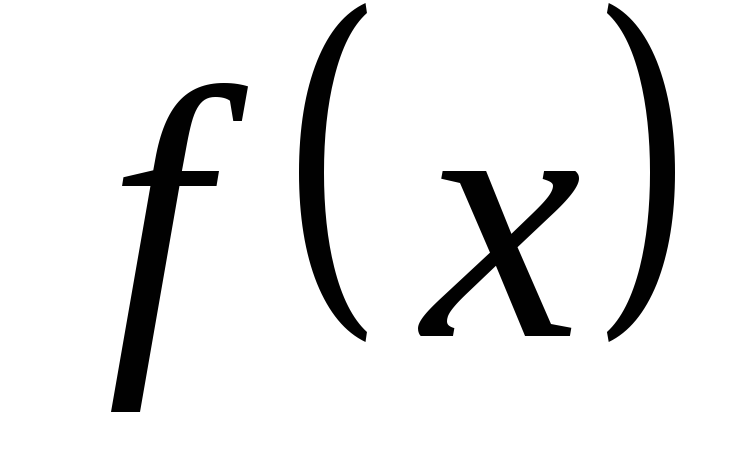в ряд Фурье в интервале
:
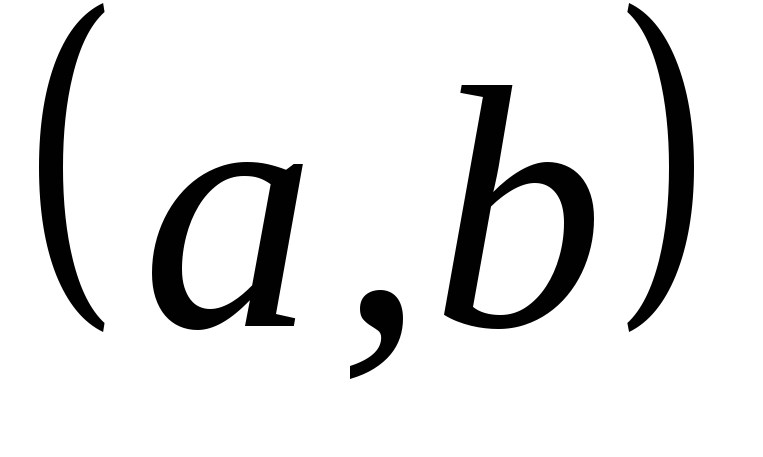а)
;
;
;
,
б)
,
в)
;
;
по синусам кратных дуг.
-
Вычислить определенный интеграл с точностью
:
.
-
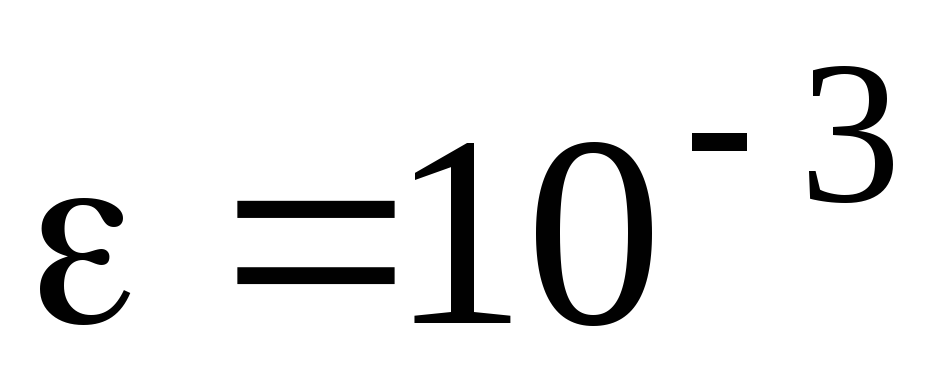Доказать равномерную сходимость на указанном отрезке:
;
.