Шпоры по рядам / ш4эм
.doc
12. Теорема о
виде остаточного члена ряда Тейлора
Пусть действ. f(x)
определена в окрестности хо и имеет в
ней производные всех порядков, тогда
ряд ∑ f^n(xo)/n!
* (x-xo)^n
называется рядом Тейлора в точке хо.
Если f(x)
(n+1)
раз непрерывно диф-ма на интервале
(xo-h,xo+h),
h>0,
то остаточный член r
n(x)
ее ряда можно записать в виде
Д-во:
Построим вспомогательную функцию
Д-во:
Мo
и М1 можно соединить ломанной из D.
Если последовательно перебирать вершины
ломаной, то найдется такая сторона, на
концах которой ф-ция принимает разные
знаки. Будем считать, что Mo,
M1
– концы стороны. x=xo+t(x1-xo),
y=yo+t(y1-yo),
где o<t<1
Если т. М(х,у)
передвигается вдоль этой стороны, то
первоначальная ф-ция превращается в
ломаную ф-цию от t.
f(t)=f(xo+t(x1-xo),
yo+t(y1-yo));
очевидно, что F(t)
непрерывна.
Существует
промежуточная точка t’,
где F(t’)=0;
мы нашли M’(x’,y’)
в f(M’)=0;
13. Функции
непрерывные в области. Теорема Больцано
-Коши
Пусть f(x1..xn)
непрерывна в каждой точке множ-ва M
n-го
пространства, тогда она непрерывна и
в самом множестве.
Теорема
Больцано-Коши
Пусть f(x,
y)
определена на непрерывна в некоторой
связной области D.
Если в 2 точках Mo(xo,yo),
M1(x1,y1),
f(xo,yo)<0,
f(x1,y1)>0
функция принимает значения разных
знаков, то в этой области существует
точка M’(x’,y’),
в которой ф-ция обращается в 0.
(вместо
a=xo)
(3) тогда (а)=f(x)(x)=f(x)+f
`(x)(x-x)+..=f(x)
(a)=f(x)
и (x)=f(x).
Тогда по т-ме Ролля найдется точка
в которой ’()=0.
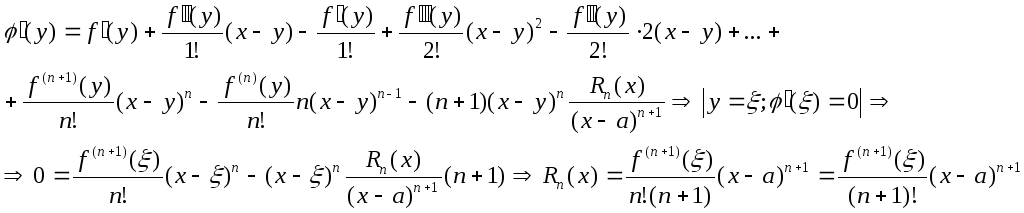получим
’()=0.
Д-во:
ΔU=f(xo+Δx,
yo+Δy,
zo+Δz)-
f(xo,yo,
zo)=[
f(xo+Δx,
yo+Δy,
zo+Δz)-
f(xo,yo+Δy,
zo+Δz)]+[
f(xo,
yo+Δy,
zo+Δz)-
f(xo,yo,
zo+Δz)]+[
f(xo,
yo,
zo+Δz)-
f(xo,yo,
zo)]=
f(x)'(xo+өΔx,
yo+Δy,
zo+Δz)Δx+
f(y)'(xo,
yo+өΔy,
zo+Δz)Δy+
f(z)'(xo,
yo,
zo+өΔz)Δz.
f(x)'(xo+өΔx,
yo+Δy,
zo+Δz)=
f(x)'(xo,
yo,
zo)+a;
f(y)'(xo,
yo+өΔy,
zo+Δz)=
f(y)'(xo,
yo,
zo)+b;
+ f(z)'(xo,
yo,
zo+өΔz)=
+ f(z)'(xo,
yo,
zo)+c;
a,b,c
зависят от Δх, Δy,
Δz.
Если Δ,x,y,z→o,
то a,b,c→0;
равенство (1)
14. Полное
приращение функции. Теорема о полном
приращении
Пусть x=xo,
y=yo,
x=xo.
Придадим переменным приращение Δx,
Δy,
Δz.
Получим
ΔU=Δf(xo,yo,zo)=f
(x)’
(xo,yo,zo)Δx+
f
(y)’
(xo,yo,zo)Δy+
f
(z)’
(xo,yo,zo)Δz+aΔx+bΔy+cΔz
(1)
Теорема:
если частные производные f(x)’(x,y,z),
f(y)’(x,y,z),
f(z)’(x,y,z)
существуют не только в точке (xо,yо,zо),
но и в некоторой окрестности и кроме
того непрерывна как ф-ии от x,y,z,
то имеет место формула (1)
получим