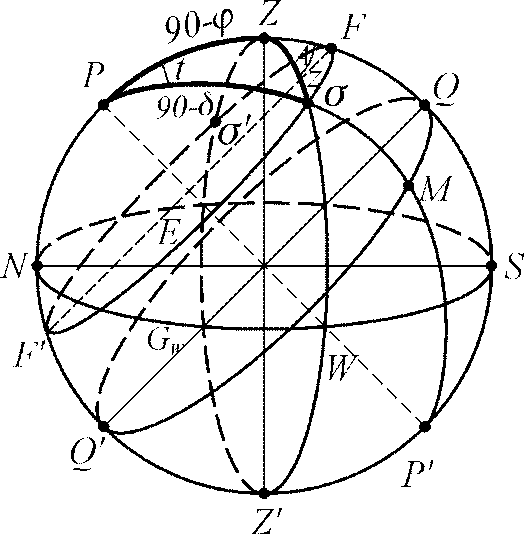
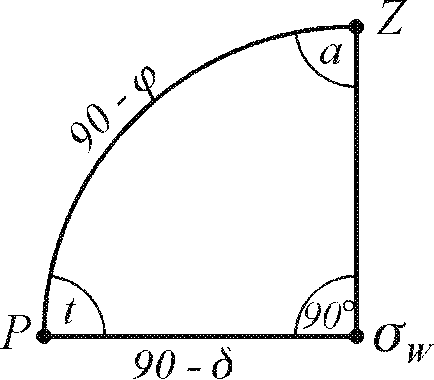- •5. Небесна сфера. Основні точки і круги небесної сфери.
- •6. Географічна система координат.
- •7. Горизонтальна система координат
- •8. Перша екваторіальна система координат
- •9 .Екліптична система координат
- •10. Зв'язок між першою і другою екваторіальними системами координат. Формула зоряного часу.
- •11. Зв’язок між географічною і першою екваторіальною системами координат.
- •12.Класифікація зірок за добовим рухом.
- •13 Визначення часу і горизонтальних координат зірок в точках кульмінації.
- •14.Визначення часу і горизонтальних координат в точках заходу і сходу світил.
- •15.Визначення часу і горизонтальних координат зірок через заданий альмукантарат.
- •16.Визначення часу і горизонтальних координат зірок в першому вертикалі.
- •18. Видимий добовий і річний рух Сонця
- •19. Дослідження видимого руху зірок
16.Визначення часу і горизонтальних координат зірок в першому вертикалі.
В
своєму видимому добовому русі світила
перетинають або не перетинають площину
першого вертикала .Умова, при збереженні
якої добова паралель зірки буде
перетинатись з першим вертикалом, буде
![]() .
.
Приймаємо, що для заданого світила відомими є його екваторіальні координати і , а також відомою є географічна широта точки спостереження
. Рисунок 3.3 – Проходження зір через І-й вертикал |
Розрахуємо
для точок
і
Відомо, що першим вертикалом називається великий круг небесної сфери, що проходить через прямовисну лінію перпендикулярно до площини небесного меридіану.
|
З
площиною небесного горизонту перший
вертикал перетинається по лінії
![]() ,
утворюючи точки заходу
і
сходу
.
Тому азимут західної частини першого
вертикала
,
утворюючи точки заходу
і
сходу
.
Тому азимут західної частини першого
вертикала
![]() становитиме 90,
а східної частини
становитиме 90,
а східної частини
![]() – 270º.
Таким чином,
– 270º.
Таким чином,
![]()
Визначаємо
зенітну віддаль світила
:

Це
значення зенітної віддалі буде однаковим
як для точки
,
так і для точки
![]() ,
оскільки
вони розміщені на одній і тій же зенітній
відстані. Тому маємо для точок
і
,
оскільки
вони розміщені на одній і тій же зенітній
відстані. Тому маємо для точок
і
![]()
Для визначення часу, коли зірка буде знаходитись в точці (західна півкуля) і точці (східна півкуля) встановимо, величину годинного кута .
![]() ,
,
![]()
Годинний кут для західної частини небесної сфери:
tw=t,
te=24h-t.
17.Визначення часу і горизонтальних координат світил в точках елонгації
Рисунок 3.5 – Елонгація світил |
Розглянемо
видимий добовий рух світил, у яких
Тоді
|
Розглянемо
видимий рух такого світила по добовій
паралелі і зміну його азимутів. В точці
верхньої кульмінації
азимут даного світила буде дорівнювати
180
і при русі світила за ходом годинникової
стрілки з точки
до точки
буде зменшуватись і в точці
досягаючи мінімального значення. Після
проходження точки
азимут світила буде збільшуватись і в
точці нижньої кульмінації
знову досягне значення 180.
При подальшому русі по добовій паралелі
азимут світила буде збільшуватись і
досягне максимального значення в точці
.
На ділянці добової паралелі
![]() величина азимута буде поступово
зменшуватись і в точці верхньої
кульмінації
знову досягне величини 180.
величина азимута буде поступово
зменшуватись і в точці верхньої
кульмінації
знову досягне величини 180.
Таким
чином, світило схилення якого
,
у своєму видимому добовому русі завжди
проходить через дві точки, азимут яких
досягає екстремальних значень: в точці
він
мінімальний, в точці
![]() – максимальний.
– максимальний.
Точки небесної сфери, в яких азимут світил, що не перетинають у своєму видимому добовому русі площини першого вертикала, набуває мінімального і максимального значень, називаються точками елонгації світила. Відповідно точка – точка західної елонгації і точка – точка східної елонгації.
В точках елонгації вертикал світила перетинається з кругом його схилення під прямим кутом.
Рисунок 3.6 – До визначення ефемерид світил в точках елонгації |
Ефемеридні координати світила в цих точках будемо визначати на основі відомого значення широти точки спостереження і відомих екваторіальних координат світила і .
Щоб
визначити зенітну відстань
,
азимут
і зоряний час
світила в точках елонгації, розглянемо
сферичний трикутник
|
Оскільки
трикутник
![]() прямокутний, то за правилом Непера,
застосувавши його до сторони
,
знаходимо:
прямокутний, то за правилом Непера,
застосувавши його до сторони
,
знаходимо:
![]()
І
звідки
![]()
або
![]() На
основі законів симетрії встановлюємо,
що
На
основі законів симетрії встановлюємо,
що
![]() тобто
для точок західної і східної елонгації
зенітні відстані будуть однакові.
тобто
для точок західної і східної елонгації
зенітні відстані будуть однакові.
Для
визначення азимута світила в точках
елонгації обчислюємо величину допоміжного
кута
![]() (рис. 3.6), користуючись правилами Непера,
застосувавши їх до сторони
(рис. 3.6), користуючись правилами Непера,
застосувавши їх до сторони
![]() (рис. 3.6).
(рис. 3.6).
Встановимо, що
![]()
і
звідси
![]() ;
;
або
![]()
Тоді, виходячи з визначення азимута, встановлюємо, що в точках елонгацій азимути можна знаходити за формулами
![]() (3.30)
(3.30)
Застосовуємо
до визначення елемента
сферичного трикутника
![]() (рис. 22) правило Непера .
(рис. 22) правило Непера .
Отримаємо
![]() (3.31)
(3.31)
і
![]() (3.32)
(3.32)
Формула
(3.31) має зміст, коли
![]() тобто
тобто
![]() ,
а значить
,
а значить
![]() (3.33)
(3.33)
Умова (3.33) є умовою елонгації світил.
Годинні кути світила в точках елонгацїі визначаються через табличний годинний кут з виразів
![]()
і
![]()
а зоряний час в точках елонгації за формулою:
![]() (3.34)
(3.34)