168

5. Нелинейные цепи.

П р и м е р 5.1 Линейный элемент с сопротивлением

R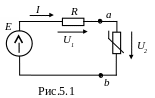 = 200 Ом и нелинейный элемент (НЭ), вольт-амперная характеристика (ВАХ) которого задана данными табл.1, соединены последовательно и подключены к источнику питания с ЭДС Е = 200 В (рис.5.1). Определить ток в цепи и напряжение на нелинейном элементе.

Таблица 1

U, В	0	20	40	60	80	100	120	160	200	240
I, А	0	0,22	0,36	0,45	0,53	0,60	0,65	0,76	0,80	0,85

Р е ш е н и е.Воспользуемся методом пересечения характеристик – графическим решением задачи.

П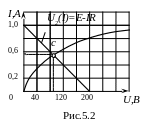 о второму закону Кирхгофа уравнение напряжения для рассматриваемой цепи имеет вид U_ab = Е – RI. Нелинейный элемент имеет ВАХ U_ab = U₂( I ). Точка пересечения характеристик определяет решение этой системы уравнений.

Строим зависимость U₂( I ), заданную табл.1 (рис.5.1). На том же графике строим линейную зависимость U_ab = Е – RI по двум точкам с координатами U_к = 0, I_к = Е/R = 1 А и I_х = 0, U_x = E = 200 В. В точке пересечения с определяем ток в цепи I = 0,55 А и напряжение на нелинейном элементе U = 85 В.

П р и м е р 5.2 Найти в аналитической форме зависимость отношения ∆U_вх / ∆U_вых от параметров балластного резистора R_б и стабилитрона VD в схеме стабилизации напряжения рис. 5.3,а.

Р е ш е н и е. В режиме стабилизации напряжения стабилитрон работает на линейном участке его ВАХ: I_{ст min} < I_ст < I_{ст max} (рис.5.3,б), при этом схема рис.5.3,а может быть заменена эквивалентной линеаризованной схемой рис.5.3,в (параметры Е_эк и

R_эк = R_диф схемы определяются графически для линейного участка ВАХ стабилитрона).

Рис5.3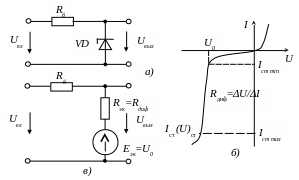

Для схемы рис.5.3,в справедливо уравнение U_вх = U_вых + R_бI.

Так как I = (U_вых – Е_эк) / R_эк, то можно записать

U_вх = U_вых + (R_б / R_эк)(U_вых – Е_эк).

Продифференцировав полученное выражение для U_вх по выходному напряжению, находим

∂U_вх/∂U_вых=1+R_б/R_эк=1+R_б/R_диф.

Так как в схеме стабилизации напряжения выполняется неравенство R_б>>R_диф, окончательно имеем

∆U_вх / ∆U_вых = ∂U_вых/∂U_вых = R_б/R_диф.

Коэффициент стабилизации напряжения в схеме рис. 5.3 возрастает с увеличением сопротивления балластного резистора и уменьшением дифференциального сопротивления стабилитрона.

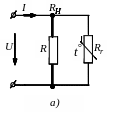
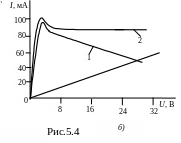
П р и м е р 5.3 На рис. 5.4,а, представлена цепь содержащая позистор СТ5-1, ВАХ которого показана на рис. 5.4,б (кривая 1), и линейное сопротивление R.

Подобрать величину R так, чтобы цепь могла быть использована как стабилизатор тока. Построить входную ВАХ I(U) и определить ток стабилизации.

Р е ш е н и е. Чтобы цепь рис. 5.4,а работала как стабилизатор тока, нужно подобрать такое сопротивление R, при котором суммарная ВАХ параллельной цепи имеет горизонтальный участок (I=сonst). Это достигается при равенстве сопротивления R модулю дифференциального сопротивления позистора на падающем участке. Следовательно, на участке 8  U  32 В (см. рис. 5.4,б) дифференциальное сопротивление позистора R_д=ΔU/ΔI= –600 Ом, тогда R=|R_д|=600 Ом.

Ток стабилизации можно определить аналитически для любого значения напряжения на данном участке, например для U=8 В:

I_ст=I_нс+I_R=80+(8/600)·10³=93,3мА.

Ток стабилизации можно получить графически, сложив ординаты ВАХ позистора и сопротивления R. При этом получим кривую 2, которая представляет входную ВАХ I(U).

П р и м е р 5.4 Катушка с кольцевым сердечником, содержащим воздушный зазор, подключена к сети постоянного тока напряжением U=12 В. Обмотка катушки имеет сопротивление R = 12 Ом и число витков w = 1000. Сердечник выполнен из стали 1512 и имеет внешний диаметр D = 22 см, внутренний диаметр d = 18 см, толщину пакета b = 1 см, коэффициент заполнения стали k_з.с.≈ 1. Определить магнитный поток и индуктивность катушки, если воздушный зазор сердечника δ₁ = 0,01 см, и начертить схему замещения магнитной цепи.

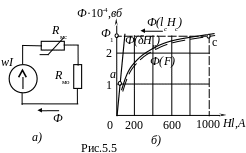Р е ш е н и е. Схема замещения магнитной цепи аналогична схеме последовательной электрической цепи. Аналогом тока является магнитный поток, аналогом ЭДС является МДС Iw, аналогом линейного сопротивления – магнитное сопротивление воздушного зазора, аналогом нелинейного сопротивления – магнитное сопротивление магнитопровода (рис.5.5,а).

Магнитодвижущая сила для заданного сердечника определяется уравнением wI = l_cH_c + δH_н, которое можно решить графическими методами: 1) построением суммарной вебер-амперной характеристики; 2) пересечением вебер-амперных характеристик (аналогично методам решения уравнений нелинейных электрических цепей постоянного тока). Рассмотрим оба метода решения.

1) Вычисляем индукцию В, задаваясь произвольно несколькими значениями потока Ф в сердечнике и зная поперечное сечение сердечника см². Затем по кривой намагничивания (табл. 2) находим соответствующие значения Н_с и вычисляем l_cH_c, где длина магнитной линии по стали см.

Кривая намагничивания стали 1512

Таблица 2

В.Тл	0,2	0,4	0,5	0,75	1,0	1,2	1,34
Н, А/м	40	100	125	240	440	800	1650

Полученные результаты расчетов сведены в табл. 3.

Таблица 3

Ф∙10-4, Вб В, Тл Нс, А/м LcHc, А

0,84 0,42 100 62,8

1,0 0,5 125 78,4

1,5 0,75 240 151

2 1 440 276

2,2 1,1 575 361

2,4 1,2 850 534

2,48 1,24 1000 628

2,68 1,34 1650 1035

На основании данных таблицы и схемы замещения (рис.5.5,а) строим вебер-амперную характеристику Ф (l_cH_c) (рис.5.5,б ). Далее строим линейную зависимость – вебер-амперную характеристику воздушного зазора Ф (δН_в). Для этого определяем координаты одной точки: например, для В = 0,5 Тл и δ₁= 0,01 см находим

Ф₁ = BS = 1∙10^-4 Вб, Н_в = В/μ₀= 4∙10⁵ А/м и Н_вδ = 40 А. Откладываем на графике точку а с координатами Ф₁ = 1∙10^-4 Вб и lH = 40 А. Проводим через начало координат и точку а искомую прямую Ф (δН_в). Затем в соответствии со схемой замещения (рис. 5.5,а) производим сложение абсцисс кривых Ф(l_cH_c) и Ф(δН_в) и получаем суммарную кривую Ф(F) (обозначена пунктиром), где F = lH – МДС.

Заданную МДС А откладываем на оси абсцисс, восставляем перпендикуляр до пересечения в кривой Ф(F) в точке с. От этой точки проводим горизонтальную линию до пересечения с осью ординат. Получаем искомое значение магнитного потока Ф₁ = 2,62∙10^-4 Вб;

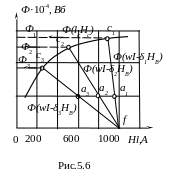2) Другой метод целесообразно применять для нахождения магнитного потока при различных зазорах. При этом на графике с построенной вебер-амперной характеристикой Ф_с =(I_cH_c) строим прямые Ф(wI – δ_iH_в), соответствующие заданным воздушным зазорам δ_i (рис. 5.6), по двум точкам. Для этого нужно предварительно определить напряженность поля Н_в для одного из значений индукции (или магнитного потока). Определим, например, Н_в для индукции В = 0,5 Тл (что соответствует магнитному потоку Ф = 1∙10⁴ Вб): Н_в = 8∙10⁵∙В = 4∙10⁵ А/м. Тогда δH_в = 40 А, wI – δ₁H_в = 960 А.

Находим на графике рис.5.6 точку а₁, с ординатой Ф = 1∙10^-4 Вб, абсциссой lH = 960 А и проводим через нее и точку f прямую. Точка с₁ пересечения кривой Ф(l_cH_c) и прямой Ф(wI – δ₁H_в) определяет искомое значение потока Ф₁ = 2,62∙10^-4 Вб при зазоре δ₁= 0,01 см. Для других зазоров аналогично через точки а₂ и а₃ проводят прямые до пересечения с кривой Ф_с =(I_cH_c) и определяют величины потоков Ф₂ и Ф₃.

Индуктивность катушки при зазоре δ₁= 0,01 см равна

L = wФ₁/I = 262 мГн.

П р и м е р 5.5 На магнитопровод, размеры которого в миллиметрах приведены на рис. 5.7, а намотана обмотка с числом витков w= 100. По обмотке протекает ток 2А. Определить магнитную индукцию в воздушном зазоре. Площадь сечения воздушного зазора считать равной площади сечения магнитопровода, δ = 1 мм, кривая намагничивания материала задана таблицей 4.

Табл. 4

В,Тл	0,25	0,6	0,7	0,8	0,9	1,1	1,25	1,35	1,4	1,45	1,5	1,6	1,7	1,8	1,9	2,0
H,А/м	50	88	113	138	170	250	530	1000	1500	2800	4200	7800	13000	23000	34000	70000

Р е ш е н и е. Задачу решаем графически на основании закона полного тока для магнитной цепи: Iw=Hl_ср+0,8·10⁶В·2δ=U_м∑.

З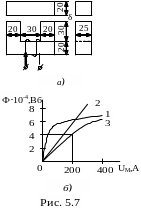 десь первое слагаемое определяет падение магнитного напряжения в магнитном материале, второе - падение магнитного напряжения в воздушном зазоре. Значение индукции берется в теслах, длина зазора - в метрах.

Строим вебер-амперную характеристику магнитной цепи Ф(U_м∑). Определяем сечение магнитопровода S=20·25=500 мм² и среднюю длину магнитной цепи l_ср=30+50+30+50=160 мм.

Пользуясь кривой намагничивания (или таблицей 1) определяем несколько значений U_м= Hl_ср и соответствующие им величины Ф = ВS.

Зависимость потока от падения магнитного напряжения в стали, построенная на основании соотношений Ф=ВS, U_м= Hl_ср, приведена на рис. 5.7, б (кривая 1).

Зависимость магнитного потока от падения напряжения в воздушном зазоре линейна (прямая 2). Кривая 3 является результирующей вебер-амперной характеристикой всей цепи.

Таким образом, здесь наблюдается полная аналогия с нелинейной цепью постоянного тока – замена двух последовательно включенных нелинейного и линейного сопротивления одним эквивалентным нелинейным. При Iw=200A; Ф=4·10^-4 Вб; В=0,8 Тл.

П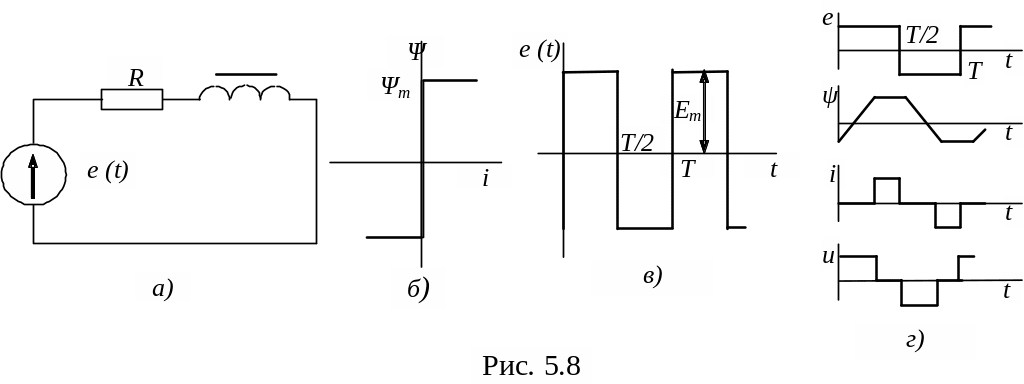 р и м е р 5.6 Построить кривые изменения во времени потокосцепления Ψ, тока I и напряжения U в схеме рис. 5.8, а.

Характеристика Ψ = f(i) изображена на рис. 5.8, б; Ψ _т=0,015 Вб. График воздействующей ЭДС е= f(t) изображен на рис. 5.8, в; E_т=100 В, период Т=9·10^-4 с; R=1000 Ом.

Р е ш е н и е. К концу отрицательного полупериода потокосцепление и ток, соответственно равны Ψ = –Ψ_т и i=0. В положительный полупериод в уравнении dΨ/dt+Ri=e(t) слагаемое Ri=0.

Когда изображающая точка перемещается по вертикальному участку зависимости Ψ = f(i), происходит перемагничивание нелинейной индуктивности. В этом интервале времени

dΨ/dt= Е и Ψ=Et+C,

где С - постоянная интегрирования.

При t=0 Ψ= –Ψ_т , отсюда С = – Ψ _т ; потокосцепление Ψ изменяется по закону Ψ = Et  –Ψ _т до момента времени t₁=2 Ψ _т/E=T/3, когда Ψ достигает Ψ _т.

В интервале от Т/3 до Т/2 потокосцепление остается равным Ψ_т;

при этом dΨ /dt=0; Ri=e(t).

Отсюда i=E/R= 0,1А. Графики требуемых величин в функции времени показаны на рис. 5.8, г.

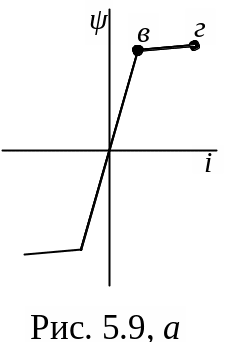
П р и м е р 5.7 Через нелинейную индуктивность, зависимость Ψ = f(i) которой изображена на рис. 5.9,а протекает синусоидальный ток I_msin ωt. Построить кривую изменения напряжения на индуктивности в функции ωt для этого случая, если I_m=1А, ω=1000 с^-1 (координаты точек в – Ψ_в=0,95 Вб, i_в=0,05 А; г - Ψ_г=1 Вб; i_г=1 А)

Р е ш е н и е. При изменении потокосцепления от

– 0,95 до 0,95 Вб (рис.5.9,а) Ψ = κ₁ i, где κ₁=0,95/0,05=19.

Н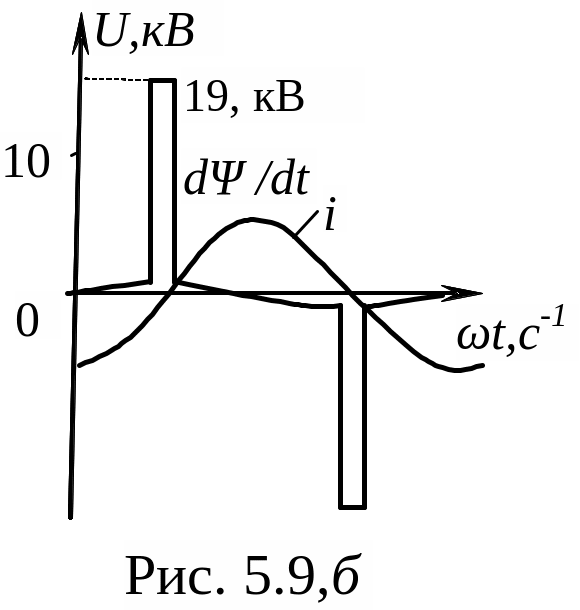 а этом участке dΨ / dt = κ₁ωI_m cos ωt=19∙10³ cos ωt.

Изменение dΨ/dt по такому закону происходит на участке

от – ωt₁ до ωt₁= arcsin 0,05=2˚53΄ (рис. 5.9, б).

На участке от 0,95 до 1 Вб Ψ= Ψ₀+ κ₂ i, где κ₂=0,05/0,95=1/19.

Здесь dΨ/dt= κ₂ωI_m cos ωt=52,7 cos ωt В.