3. Первая теорема о вариационных неравенствах

Некоторые сведения о билинейных формах:

Пусть Х− банахово пространство, F:Х→Х′, где Х′- двойственное пространство к Х, т.е. пространство всех линейных форм а: Rⁿ→R, x→ .

F:Rⁿ→(Rⁿ)′, где (Rⁿ)′− пространство линейных непрерывных функционалов над Rⁿ

π: (Rⁿ)′→Rⁿ, где π такое отождествление ,что f (Rⁿ)′ : (πf)_i= , где (e_i)_j –базис пространства Rⁿ.

Пусть x Rⁿ, то есть х=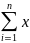 _ie_i, где e_i-базисные вектора в Rⁿ

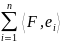= = x_i= x_i, где (πF)_i= , i=1,n, следовательно

=(πF,x )

Теорема 3.1.

Пусть К Rⁿ – компактное выпуклое множество и F:К→(Rⁿ)′- непрерывное отображение. Тогда существует х К, такое что

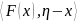≥0, η К (2.2)

Доказательство.

Pr_K: Rⁿ→K; I:K→Rⁿ, такое что Ix=x π:(Rⁿ)′→ Rⁿ ; F:K→(Rⁿ)′;

Рассмотрим отображение Pr_K (I-πF):K→K. Так как

πF:K→ Rⁿ − непрерывное отображение

I-πF:K→ Rⁿ − непрерывное отображение, то учитывая следствие 2.1, имеем

Pr_K (I-πF):К→К− непрерывное отображение, а следовательно по теореме 2.2 существует неподвижная точка х К такая что Pr_K (I-πF)(х)=х, а так как х из К, то (I-πF)(x)=x

По теореме 2.1 для любого η К выполняется неравенство

(x, η-x)≥(x-πF(x),η-x)=(x,η-x)-(πF(x),η-x).

Следовательно

(πF(x),η-x)≥0

Поэтому в силу определения отождествления π имеем

(πF(x),η-x)≥0 ≥0 η К.

Теорема доказана.

Следствие 3.1.

Пусть х – решение неравенства (3.1), принадлежащее внутренности множества К. Тогда F(x)=0.

Доказательство.

По условию следствия х- решение ≥0, y К. Так как х К, то r>0: шар B(x,r) K. Возьмем ξ Rⁿ, такое что |ξ|≤ε, ε>0.

Пусть у B(x,r) K, тогда у=х+ ξ

|y-x|=| ξ |= |ξ|≤ ε=r

Предположим, что F(x)≠0.

По теореме 3.1 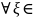Rⁿ выполняется ≥0. (3.2)

Пусть F(x) 0, так как F(x) (Rⁿ)′, то ξ₀ Rⁿ: 0, тогда ввиду (3.2) имеем

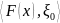>0

Возьмем элемент -ξ₀ Rⁿ, по (3.2) ≥0 следовательно, ≤0. Пришли к противоречию. Полученное противоречие доказывает, что F(x)=0.

Следствие доказано.

4. Вариационные неравенства

Рассмотрим следующую задачу

Задача(4.1)

Пусть даны выпуклое замкнутое множество К в Rⁿ и непрерывное отображение F: K→(Rⁿ)′ . Требуется найти элемент x K, такой что ≥0, y К (4.1)

Из теоремы 3.1 следует, что если R>0 и K_R=K Σ_R≠ (Σ_R− замкнутый шар в Rⁿ радиуса R с центром в нуле), то существует такое x_R K_R:

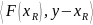≥0, y К_R (4.2)

Теорема 4.1.

Пусть К Rⁿ замкнуто и выпукло и F: K→(Rⁿ)′ − непрерывное отображение. Тогда для существования решения задачи(4.1) необходимо и достаточно, чтобы для некоторого R>0 решение (4.2) x_R K_R удовлетворяло условию: | x_R |<R

Доказательство.

Очевидно, что если х− решение задачи(4.1),то х является решением неравенства (4.2) при | x|<R.

Предположим, что для некоторого R имеем x_R K_R и| x_R |<R. Так как | x_R |<R, то для любого y К найдется такое ε>0, что w= x_R+ε(у- x_R) K_R. Следовательно, в силу (4.2)

0≤ =ε y К.

Это значит, что x_R – решение задачи (4.1). Теорема доказана.

Следствие 4.1.

Пусть отображение F: K→(Rⁿ)′ удовлетворяет условию

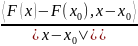→∞, при |x|→∞, x К,

для некоторого х₀ К₀, тогда существует решение задачи(4.1)

Доказательство.

Пусть |F(x₀)|<H, |x₀|<R, так что ≥H|x-x₀|, при |x|≥R, x K.

Тогда = - ≥H|x-x₀| . Поэтому

≥H|x-x₀|+ ≥H|x-x₀|-|F(x₀)||x-x₀|≥(H-|F(x₀)|)(|x|-|x₀|)>0 при |x|≥R. (4.3)

Если теперь x_R K_R−решение неравенства (4.2), то

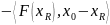= ≤0, отсюда и из (4.3) следует, что |x_R|<R, то есть x_R является решением задачи(4.1)

Следствие доказано.

Следствие 4.2.

Пусть К Rⁿ замкнуто и выпукло и F: K→(Rⁿ)′ − непрерывное отображение. Пусть для любых х, х′ К, х≠х′, выполняется условие:

>0.

Тогда решение задачи(4.1) единственно.

Доказательство.

Пусть х, х′− два различных решения задачи(4.1), тогда

≥0 у К

≥0 у К

Подставим в первое уравнение у= х′, во второе у= х и складывая их, получим:

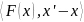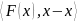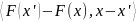+ = - = ≥0. Тогда

≤0, (4.4)

Но так как х≠х′, то в силу условия данного следствия имеем

>0

Но это противоречит (4.4). Полученное противоречие доказывает, что х=х′.

Следствие доказано.

Определение 4.1.

Отображение F: :K→(Rⁿ)′ называется монотонным, если

≥0, х,х′ К,

и строго монотонным, если равенство возможно только при х=х′

Предложение 4.1.

Пусть К₁ Rⁿ − замкнутое выпуклое множество и F:K₁→(Rⁿ)′− непрерывное строго монотонное отображение. Пусть, далее К₂ К₁, замкнуто и выпукло. Предположим, что существуют такие х_j К_j, j=1,2, такие что

≥0 у К_j, j=1,2 (4.5)

Тогда 1) если F(x₂)=0, то х₁=х₂;

2) если F(x₂)≠0 и х₁≠х₂, то гиперплоскость 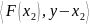=0 отделяет х₁ от К₂ , т.е. ≥0>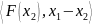 при всех у К₂.

Доказательство.

1. ≥0 и ≥0, вычтем из первого неравенства второе

- = ≥0, так как F(x₂)=0, получим ≥0.

По условию F-строго монотонно, а из определения строго монотонной функции вытекает, что х₁=х₂.

2. ≥0 , ≥0, F(x₂)≠0 и х₁≠х₂

Вычтем из первого уравнения второе:

- = = ≥0

<0, так как F-строго монотонное отображение.