6.6. Особенности регулирования момента и тока в системе г — д

Для реализации стандартной настройки на технический оптимум контура регулирования момента в системе Г—Д при последователь­ной коррекции имеются две возможности: непосредственная коррек­ция и введение подчиненного контура регулирования ЭДС генератора или его тока возбуждения.

Так же как и в системе ТП—Д, регулирование момента в системе Г—Д осуществляется с помощью отрицательной обратной связи по току якорной цепи. Структурная схема контура регулирования тока, учитывающая влияние внутренней связи по ЭДС двигателя в виде независимого возмущения по скорости, представлена на рис. 6.18, а.

Если принять, что компенсации подлежат большая постоянная Тг и средняя Тя, то Τμ = Tτ,β 0,01 с, при этом передаточная функция регулятора тока получается в виде

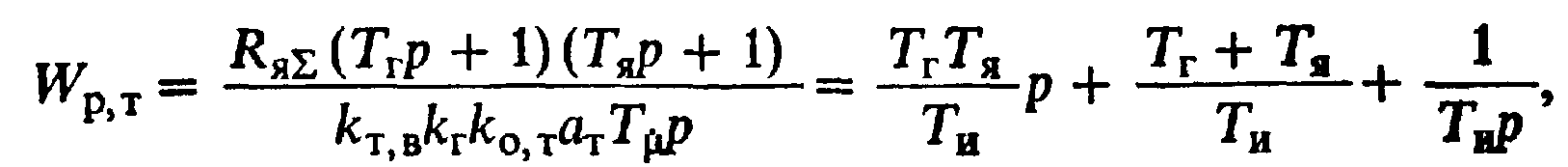(6.47)

где

Получена передаточная функция ПИД-регулятора. Свойства элект­ропривода при этом в пределах линейности системы совпадают с рассмотренными выше для системы УП—Д с быстродействующим преобразователем. Если использование ПИД-регулятора нежелательно, можно отказаться от компенсации постоянной Тя, положив Tμ= Тτ.β + Тя >0,01 с. Передаточная функция регулятора тока при этом получается в виде

(6.48)

Полученный ПИ-регулятор удобен в реализации, но увеличение суммарной некомпенсируемой постоянной Тμ= Тт,в + Тя определяет соответствующее снижение быстродействия контура и уменьшение точности регулирования. Это ухудшение свойств контура регулиро­вания тем более значительно, чем больше Тя. Поэтому при повы­шенных значенияхТ_Яболее благоприятные условия регулирования тока и момента обеспечиваются введением подчиненного контура регулирования ЭДС генератора (рис. 6.18, б).

Применив уже неоднократно использованный выше метод опре­деления передаточной функции регулятора для контура регулирования ЭДС,получим

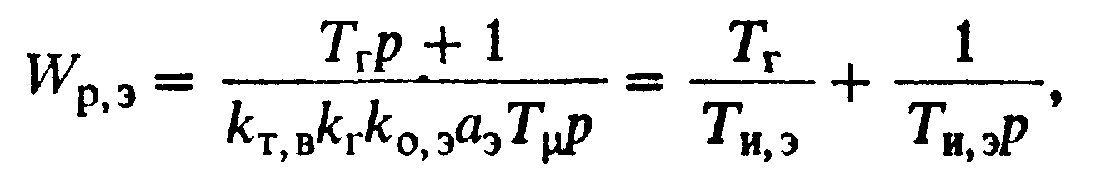(6.49)

Замкнутый контур регулирования ЭДСимеет передаточную функ­цию

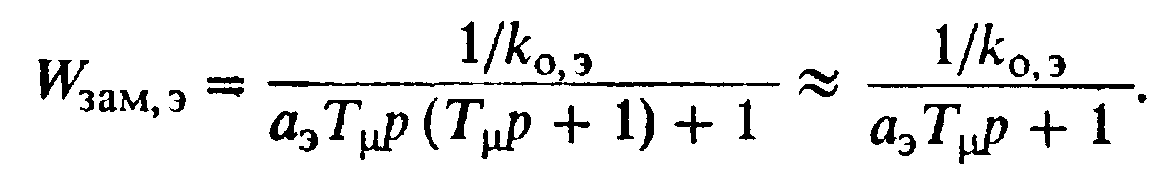(6.50)

Следовательно, благодаря введению подчиненного контура регу­лирования ЭДС передаточная функция объекта регулирования тока принимает вид

(6.51)

В контуре регулирования тока якоря осталась одна подлежащая компенсации постоянная Тя, но некомпенсируемая инерционность кон­тура возросла: Τμт = а_ЭТμ. Отсюда регулятор тока должен иметь следующую передаточную функцию:

(6.52)

Таким образом, введение подчиненного контура регулирования ЭДС позволяет ограничиться применением ПИ-регуляторов. Получен­ная в результате коррекции передаточная функция замкнутого кон­тура тока якоря имеет вид

(6.53)

При настройке на технический оптимум (а_Э = а_Т= 2) динамические свойства контура регулирования тока качественно получаются такимиже,как и в системе с быстродействующим преобразователем, однако количественно быстродействие контура и точность регулирования тока и момента ухудшаются в 2 раза. Сравнивая вариант однокон­турной системы с ПИ-регулятором тока (6.48) с двухконтурной, можно заключить, что при Тт.в +T_Я< 2·Тт,в быстродействие и точ­ность регулирования в одноконтурной системе выше, чем в двухконтурной. При Тт,в + Тя>2Тт,в предпочтителен вариант двухконтур­ной системы, особенно в тех случаях, когда возможность ограничения максимальной ЭДС генератора представляет практический интерес.

Для ограничения ЭДС генератора значением Е_ГЕ_Гmaxв струк­туре на рис. 6.18, б достаточно ограничить выходное напряжение регулятора тока, которое является сигналом задания ЭДС генератора, значениемU_З.Эmax.

Весьма большая постоянная времени генератора Тр является важной особенностью системы Г-Д. Необходимо иметь в виду, что компенсация постоянной Τι-исключает эту инерционность из контура только математически. Физически она в контуре регулирования при­сутствует, и ее влияние компенсируется соответствующим форсиро­ванием напряжения возбуждения только в пределах, ограниченных предусмотренным запасом по напряжениюU_В.MAX= α·U_В.ном.

Высокое быстродействие контура регулирования при стандарт­ной настройке требует соответственно быстрых изменений ЭДС ге­нератора. Для изменения ЭДС генератора по закону е_Г=(de_Г/dt)_maxt=(de_Г/dt)_max/р к его обмотке возбуждения в соответствии с передаточной функцией необходимо приложить напряжение

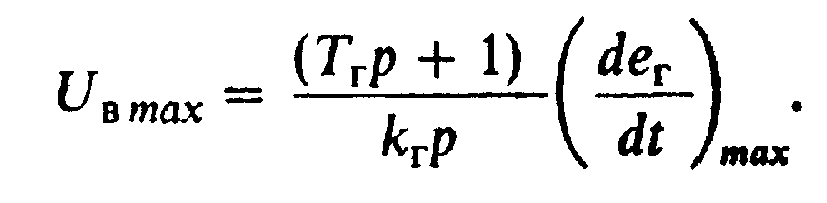(6.54)

Если при этом Е_Г <<Ег ном. (6.54) можно упростить:

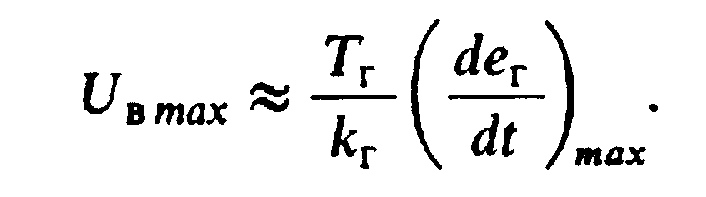(6.55)

Этим же соотношением можно воспользоваться для определения требуемых форсировок возбуждения генератора для изменения ЭДС генератора по синусоидальному законуе_Г= ΔЕ_ГmaxsinΩt,при этом

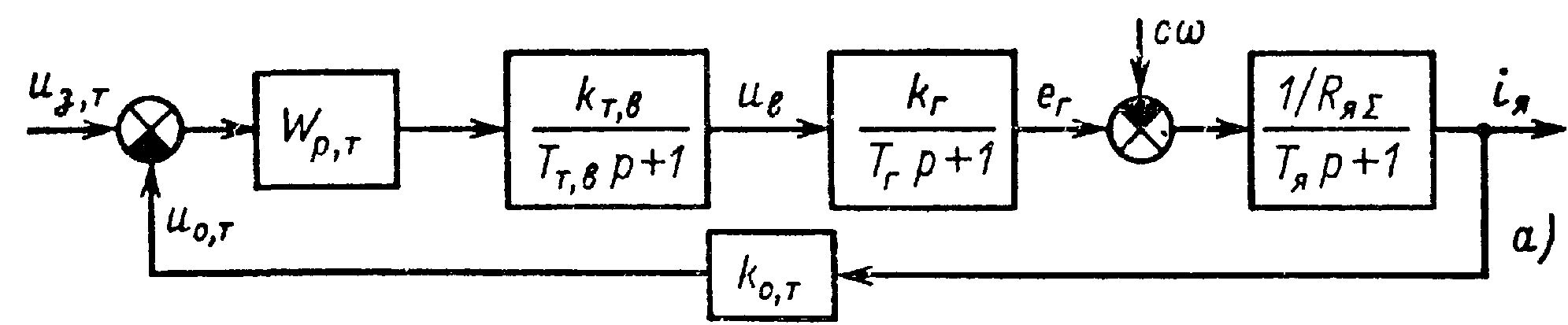
Рис.6.18. Структурные схемы при последовательной коррекции конту­ра регулирования тока в системе Г — Д

подстановка в (6.55) амплитуды производной от е_Гдает

(6.56)

Уравнение (6.56) свидетельствует о том, что в связи с большим значением Тг напряжение U_В.MAXдолжно быстро возрастать с увели­чением частоты и амплитуды колебаний ЭДС. Пренебрегая насыще­нием магнитной цепи генератора, с помощью (6.56) оценим требуемый запас по напряжению возбуждения на частоте среза контура регули­рования тока, настроенного на технический оптимум:

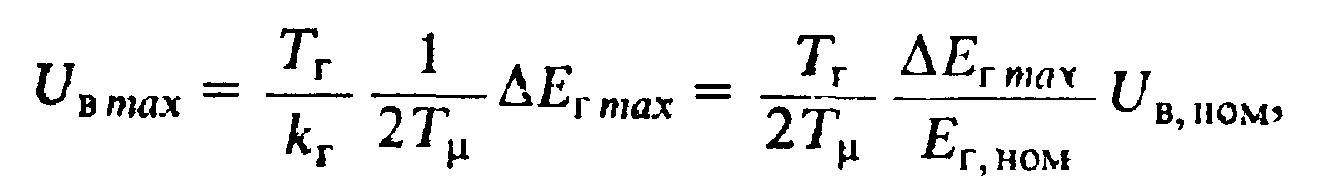(6.57)

где

Следовательно, в данном режиме требуется коэффициент форси­рования

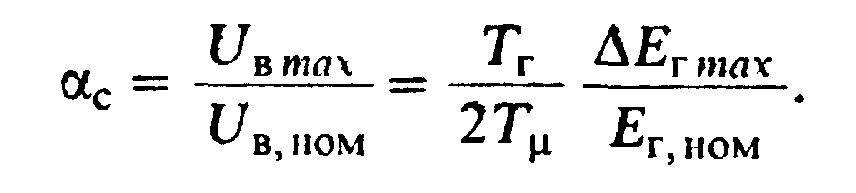(6.58)

При ограниченном запасе по напряжению возбудителя αпределы частот и амплитуд колебаний, в которых система Г—Д остается линейной системой, ограниченны:

(6.59)

Если условие (6.59) не выполняется, система регулирования яв­ляется нелинейной, главным образом, из-за нелинейности характе­ристики возбудителя. При этом все полученные выше оценки быстро­действия и точности регулирования могут быть недостаточно досто­верными. Поэтому при проектировании электроприводов по системе Г—Д с последовательной коррекцией контуров регулирования ЭДС, тока якоря и других координат системы необходимо проверять достаточность принятого запаса по напряжению возбудителя для реализации стандартных показателей регулирования.

С помощью уравнения электрического равновесия якорной цепи Г-Д

можно определить производную ЭДС генератора как функцию регу­лируемой координаты:

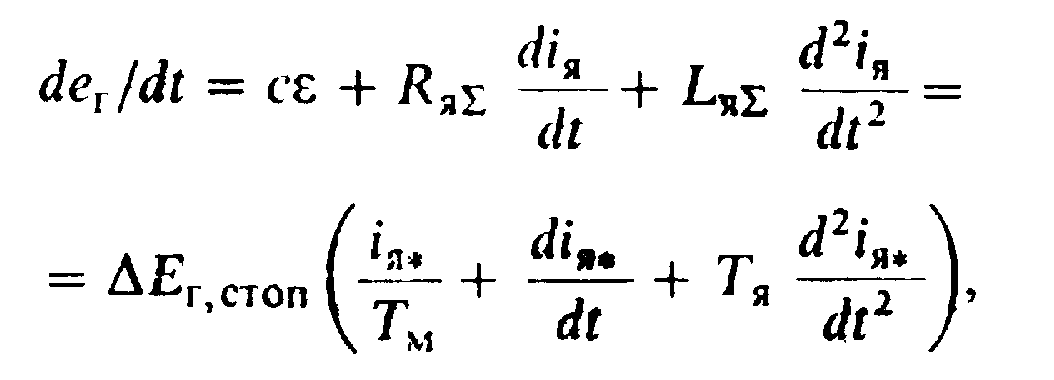(6.60)

где

Зависимость i_Я=f(t)при настройке натехнический оптимум определяется соотношением (5.32):

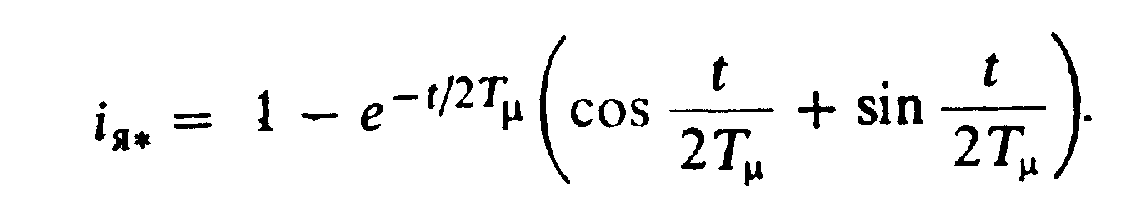(6.61)

Соответствующие зависимости di_Я/dt=f(t)иd²i_Я/dt²=f(t)мо­гут быть получены с помощью (6.61). Подстановка этих зависимостей в (6.60) позволяет рассчитать кривуюde_Г/dt=f(t), определить по ней (de_Г/dt)maxи далее с помощью (6.55) вычислить требуемое максималь­ное напряжение возбудителяU_В.MAX=α_ТР·U_В.НОМ.

Если полной реализации возможного при настройке на техни­ческий оптимум быстродействия не требуется, можно ограничиться выбором α_ТРпо заданному времени пуска (см. § 5.3). При этом для определения динамических показателей качества и точности регули­рования необходим расчет переходных процессов в системе с учетом основных нелинейностей, который целесообразно выполнять с по­мощью ЭВМ.