6.4. Автоматическое регулирование момента в системе уп—д

Общий анализ свойств регулируемого электропривода, замкнутого отрицательной обратной связью по электромагнит­ному моменту, целесообразно провести с помощью обобщен­ной структурной схемы на рис. 5.12,6, дополнив ее цепью указанной обратной связи. При этих условиях структурная схема имеет вид, показанный на рис. 6.9, и позволяет записать следующую систему уравнений механической характеристики электропривода:

(6.22)

Путем преобразования системы (6.22) получим уравнение механической характеристики электропривода в виде зависи­мости момента от скорости:

(6.23)

Уравнение статической механической характеристики полу­чим из (6.23) при p=0:

(6.24)

где Мкз = Uз,м·k`<sub>П</sub>βе/(1 + βе·k<sub>о.м</sub>·k`_П) — момент короткого замыкания;

βз.м = βе/(l+ β_С·k_о.м·k`_П)- модуль статической жесткости;

ω_0З.М=Uз,м·k`_П/с —скорость идеального холостого хода в замкнутой системе регулирования.

Примем, что необходимо получить при ω=0 заданное зна­чение момента стопорения электропривода Мкз=Мстоп- Это значение может быть получено при различных коэффициентах обратной связи по моменту путем выбора соответствующих значенийU_З.М.с помощью соотношения

Семейство механических характеристик электропривода, со­ответствующее Мк,з=Мстоп=const при k_o,м=var, приведено на рис. 6.10,а.Рассматривая его, можно установить, что ста­тическая точность регулирования момента в данной схеме при прочих равных условиях ограничена сильным возмущающим воздействием, оказываемым электромеханической связью.

Рис. 6.9. Структурная схема электропривода с обратной связью по моменту

Вследствие действия этой связи изменения скорости двигателя в замкнутой системе регулирования оказывают на момент тем более значительное влияние, чем меньше коэффициент обрат­ной связи по моменту. При возрастании k_о,м жесткость ста­тической характеристики уменьшается и при неограниченном возрастанииk_о,мм илиk`_Пстремится к нулю. Однако при реаль­ных значениях этих величин исключить существенное влияние изменений скорости на точность регулирования момента без принятия специальных мер практически невозможно.

При отсутствии обратной связи по моменту (k_о,м=0) для получения момента Мстоп необходимо небольшое значение задающего сигналаUз,м. Увеличениеk_о,мприводит к соответ­ствующему возрастаниюUз,м и задаваемой преобразователем скорости идеального холостого хода ω_0з,м. Поэтому при боль­ших коэффициентах обратной связи на форме характеристик двигателя сказывается ограничение выходной переменной пре­образователя, обусловленное в системе Г—Д насыщением магнитной цепи генератора и ограниченностью максимального напряжения возбуждения, в системе ТП — Д — необходимым ограничением предельных углов регулирования реверсивного преобразователя в выпрямительном и инверторном режимах и напряжением сети, а в системе ПЧ — АД — ограничением максимальной частоты. Если представить характеристику пре­образователя линейной зависимостьюω₀=f(Uу,ч) с идеальным ограничением максимального значения ω₀величиной ω_0max, то легко установить, что пределы изменения скорости, в которых с помощью отрицательной связи по моменту обеспечивается с той или иной точностью регулирование момента, ограничены сверху и снизу характеристиками разомкнутой системы, соответствующими ω₀=±ω_0мах=const(рис. 6 10,а).

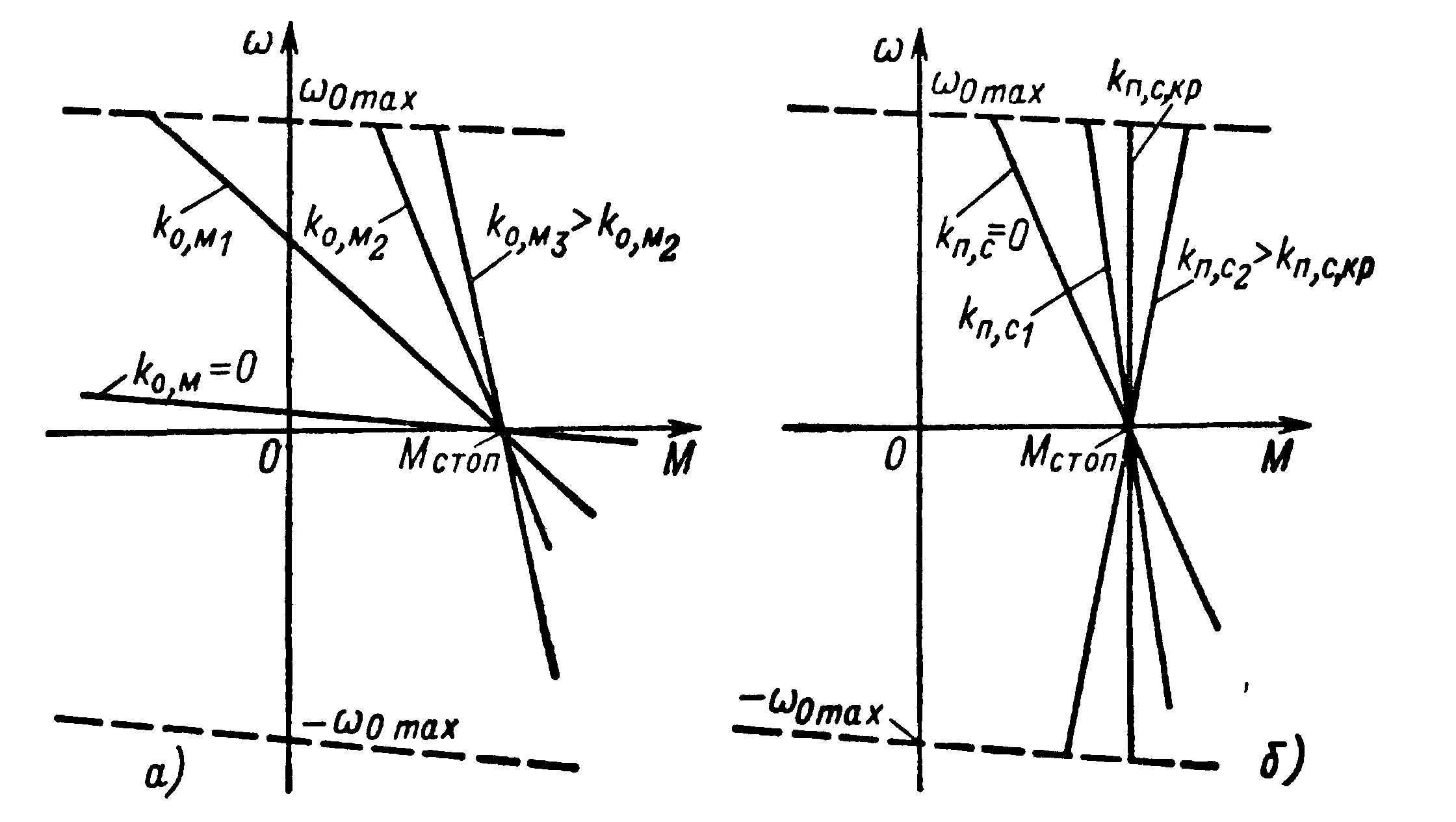
Рис. 6.10. Механические характеристики при автоматическом регу­лировании момента

В электроприводах постоянною тока вместо обратной свя­зи по моменту обычно используется обратная связь по току якоря, действие которой при Φ= Фном=const вполне анало­гично рассмотренному. При этом в полученных соотношениях коэффициентk_o,мможет быть выражен через коэффициент отрицательной связи по току якоря:

При конечных значениях коэффициентов усиления k`_Пи об­ратной связиk_o,мэффективным средством уменьшения зависи­мости момента от скорости является использование форми­рующей положительной обратной связи по скорости двига­теля, т. е. компенсационного принципа, в дополнение к основ­ной системе регулирования по отклонению. Цепь формирую­щей положительной связи по скорости показана на рис. 6.9 штриховой линией. Уравнение статической характеристики электропривода при введении этой связи можно получить из соотношений

(6.25)

где k_П.С- коэффициент положительной связи по скорости. Откуда

(6.26)

Модуль статической жесткости механической характеристи­ки в замкнутой системе зависит от коэффициента формирую­щей обратной связи по скорости:

(6.27)

При увеличении k_П,Смодуль статической жесткости быстро убывает и при критической положительной связи по скоростиk_П,С,кр=1/k`_Пстановится равным нулю. Дальнейшее увеличениеk_П,Сприводит к изменению знака жесткости, как это показано на рис. 6.10,6. При критической положительной связи стати­ческая ошибка, обусловленная изменениями скорости, исклю­чается, и система обеспечивает астатическое регулирование момента без введения в цепь регулирования регуляторов с интегральной характеристикой.

Сочетание компенсационною принципа с регулированием по отклонению дает комбинированную систему управления, обеспечивающую высокую статическую точность регулирова­ния наиболее простым путем. С помощью уравнения (6.23) при Uз,м=0 получим уравнение динамической жесткости механи­ческой характеристики в замкнутой системе:

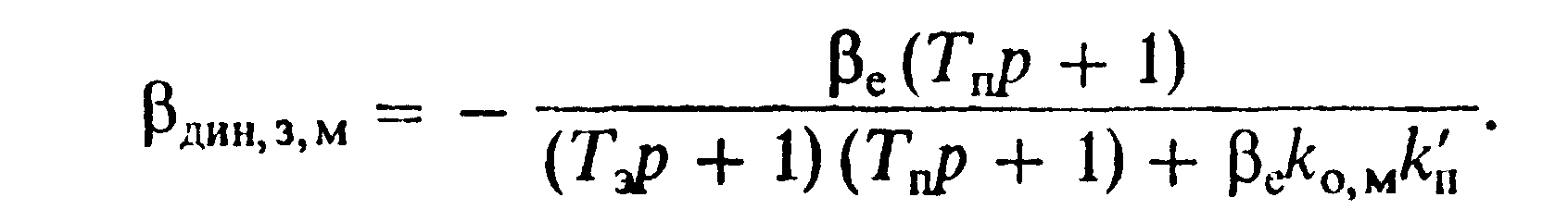(6.28)

При безынерционном преобразователе Тп=0 выражение (6.28) принимает вид

(6.29)

где β_З.М=β_C/(1+ β_C·k_O,M·k`<sub>П</sub>);Тэ.з,м =Т<sub>Э</sub>/(1 +β<sub>C</sub>·k<sub>O,M</sub>·k`_П).

Уравнение (6.29) по форме совпадает с выражением дина­мической жесткости в разомкнутой системе УП—Д, а анализ его параметров показывает, что при Тп=0 отрицательная обратная связь по моменту влияет на характеристики электро­привода так же, как введение резистора в цепь якоря двига­теля постоянного тока. Модуль жесткости βз,м при этом уменьшается и одновременно уменьшается эквивалентная постоянная времени Тэ,з,м.

На рис. 6.11, априведены ЛАЧХ и ЛФЧХ динамической жесткости, построенные по (6.29), которые подтверждают ска­занное. Динамическая жесткость в замкнутой системе при Тп=0 (кривые1и1`)снижается во всем диапазоне частот относительно жесткости в разомкнутой системе (кривые 2 и 2'), при этом точность регулирования момента в широком диа­пазоне частот остается высокой и ошибки регулирования с ростом частоты снижаются.

В случае когда Тп >> Тэ, выражение (6.28) можно представить:

(6.30)

где Тп.э - эквивалентная постоянная времени преобразователя в замкнутой системе, Тп,э=Тп/(1 + β_C·k_O,M·k`<sub>П</sub>) если приближенно принять (Тп + Тэ)/(1 + β<sub>C</sub>·k<sub>O,M</sub>·k`_П)≈Тп,э + Тэ при Тп,э > Тэ. Соот­ветствующие (6.30) ЛАЧХ и ЛФЧХ динамической жесткости замкнутой системы представлены на рис. 6.11,6. Онисвиде­тельствуют о том, что при большой Тп высокая точность регулирования момента имеет место лишь при низких часто­тах, а в области средних и высоких частот динамические свойства замкнутой системы электропривода аналогичны динамическим свойствам разомкнутой системы. Таким же путем можно убедиться, что введение формирующей положительной связи по скорости влияет на вид ЛАЧХи ЛФЧХ только в области низких частот, т. е. сказывается в основном на ста­тической точности регулирования момента.

Для анализа влияния обратной связи по моменту (току) на колебательность электропривода при жестких механических связях структурную схему рис. 6.9 с помощью (6.28) полезно представить в виде, показанном на рис. 6.12. Колебательность электропривода при Тп≈0 оценим с помощью характеристи­ческого уравнения замкнутой системы, которое можно полу­чить из передаточной функции замкнутого контура на рис. 6.12 при Μс=0 в виде

(6.31)

Нетрудно видеть, что при Тп=0 регулируемый по моменту электропривод представляет собой колебательное звено

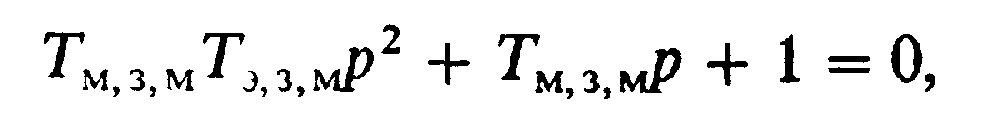(6.32)

где

Рис. 6.11 Частотные характеристики электропривода с обратной связью по моменту

Рис. 6.12. Преобразование структурной схемы электропривода с обрат­ной связью по моменту

Введение отрицательной связи по моменту увеличивает Тм,з,м и уменьшает Тэ,з,м, при этом соотношение постоянных тизменяется в сторону меньшей колебательности, а быстро­действие по моменту в связи с уменьшением Тэ.з.м увеличи­вается. Как следствие, необходимости коррекции контура регу­лирования момента при Тп=0 не возникает.

Учет инерционности преобразователя (Тп≠0) увеличивает порядок характеристического уравнения системы, что затруд­няет оценку колебательности по его корням. Динамические свойства электропривода, замкнутого обратной связью по мо­менту, удобнее проанализировать по соответствующей ЛАЧХ разомкнутого контура:

(6.33)

При Тп >> Тэ в структуре на рис. 6.12 звено динамической жесткости можно приближенно представить в виде (6.30) вместо (6.28), при этом

(6.34)

Соответствующая (6.34) ЛАЧХ показана на рис. 6.13. Ана­лизируя (6.34) и рис. 6.13, можно установить, что при неболь­ших Тм и Тп, а также при больших Тп и сильной отрица­тельной связи по моменту (Тп,э ≈Тэ) частота среза может находиться в области асимптоты с наклоном —40 дБ/дек и качество регулирования момента может быть неудовлетво­рительным.

Поэтому обычно при автоматическом регулировании мо­мента электропривода требуется коррекция динамических свойств тем или иным способом. Безкоррекции удается обойтись только в техслучаях, когда требования к быстро­действию и точности регулирования момента и тока в дина­мике невысоки. При этом необходимая точность регулирова­ния в статике обеспечивается введением критической положи­тельной связи по скорости (или по напряжению генератора в системе Г - Д), а отрицательная связь по моменту (току) ослабляется до уровня, обеспечивающего требуемое демпфиро­вание переходных процессов.

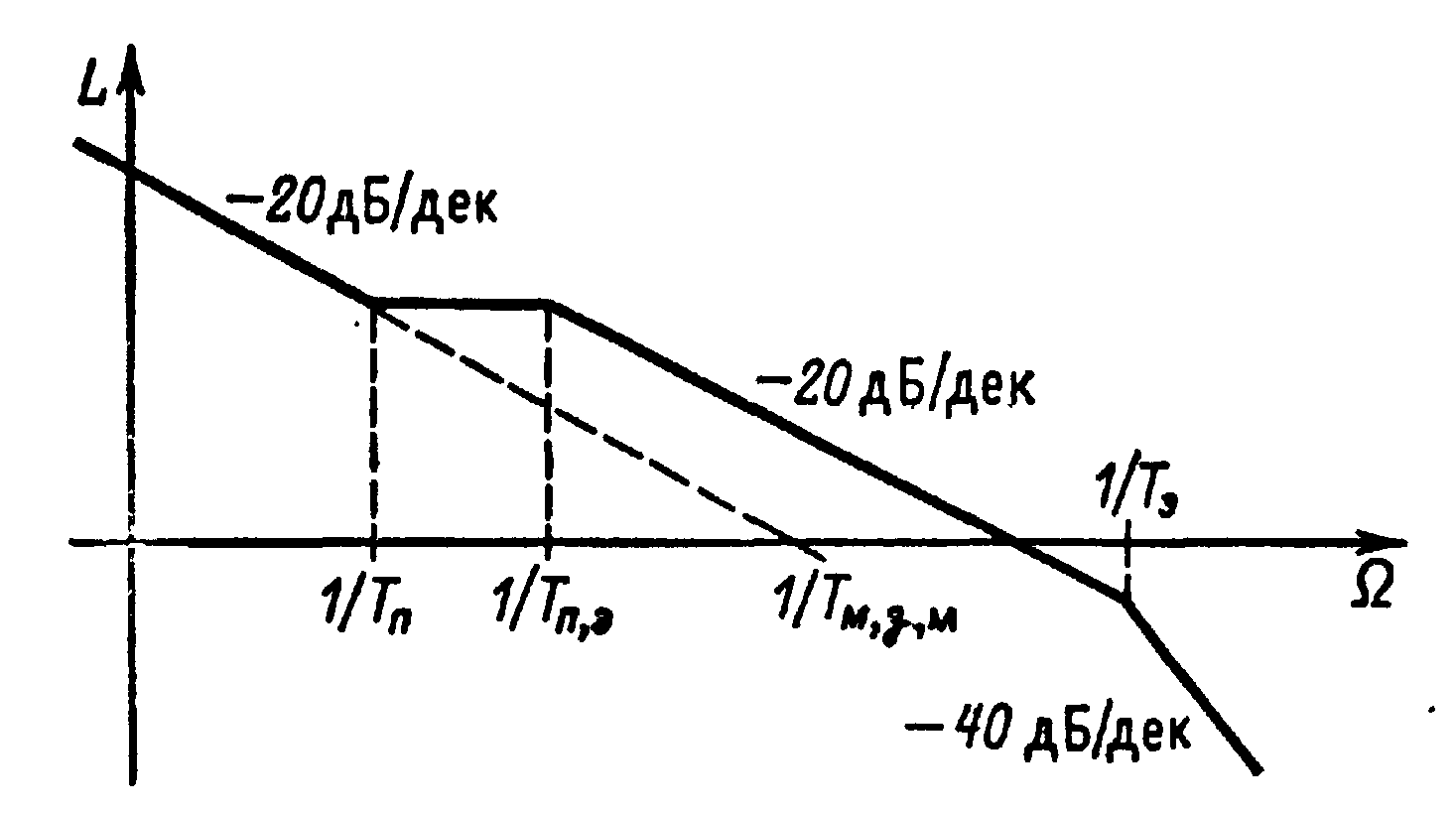
Рис. 6.13. Логарифмические амплитудно-частотные характеристики ра­зомкнутого контура регулирования момента при Тп >> Тэ