Розв’язання.

а) Так як чисельник та знаменник при дорівнюють нулю, то маємо невизначеність типу . Для того щоб розкрити цю невизначеність, розкладемо чисельник та знаменник на множники і скоротимо їх надалі на спільний множник :

.

В отриманій дробі знаменник вже не дорівнює нулю при , тому можна застосовувати теорему про границю частки:

.

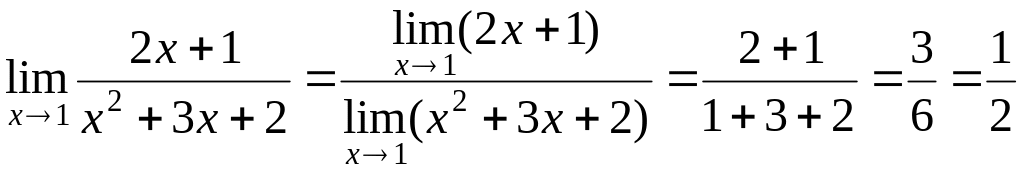Остаточно, .

б) При маємо невизначеність . Позбавимося ірраціональності в чисельнику та знаменнику. Помножимо чисельник та знаменник на вираз, спряжений до чисельника:

.

В отриманій границі невизначеність зберігається. Доповнимо знаменник дробі до різниці кубів та виконаємо необхідні перетворення:

.

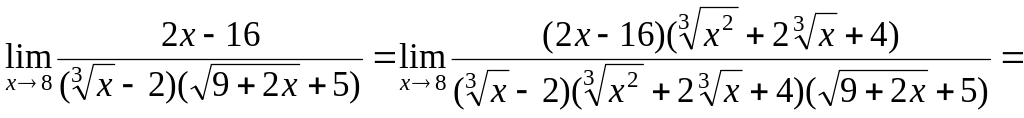
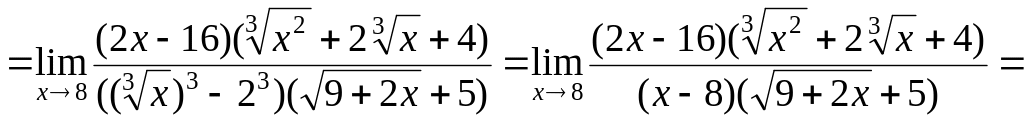
В отриманій дробі знаменник вже не дорівнює нулю при , тому можна застосовувати теорему про границю частки:

.

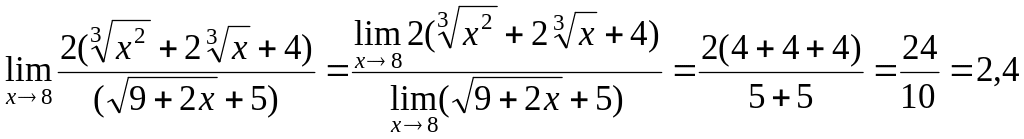Отже, .

в) Якщо , то маємо невизначеність . Розглянемо окремо знаменник дробу:

.

Маємо границю

.

Чисельник та знаменник дробу є нескінченно малими функціями при . Замінимо їх еквівалентими нескінчено малими: ~ , ~ . Тоді отримаємо

.

Отже, .

г) Зведемо дану границю до першої стандартної, зробимо заміну . Тоді при , а . Маємо

.

Перетворимо останній вираз шляхом зведення до першої визначної границі:

.

Таким чином, .

д) Якщо , то маємо невизначеність . Перетворимо чисельник та скористуємося еквівалентністю нескінчено малих, зокрема ~ , ~ , якщо :

.

Таким чином, .

е) Скористуємося властивістю границь:

.

Обчислюємо окремо кожну границю:

,

.

У першому випадку застосовуємо першу визначну границю, у другому – властивості границі.

Отже, .

Завдання 6. Довести (знайти ), що функція неперервна в точці .

Розв’язання. Зафіксуємо довільне число . Необхідно за цим ε знайти таке число , щоб з умови , тобто виходила нерівність . Значення функції в точці , тому остання нерівність набуває вигляду або .

Маємо або .

Щоб знайти , слід розв’язати останню нерівність відносно . Проте за допомогою тотожних перетворень це вдається зробити для лінійних функцій. Застосуємо прийом підсилення нерівності. Останню нерівність запишемо у вигляді

або . (*)

Підсилимо нерівність (*), замінюючи множник на число, яке він не перевищує. Для цього накладемо на шукане число обмеження . Це завжди можна зробити, оскільки залежить від ε, а число ε можна задавати як завгодно малим.

Тоді , або . Додаючи до всіх трьох частин останньої нерівності число 2, дістанемо , тому .

Замінимо в нерівності (*) множник на число 5, не порушивши при цьому знака нерівності:

.

Дістанемо, що . Отже за можна взяти менше з двох чисел 1 і . Таким чином, якщо і , то , що і завершує доведення.

Завдання 7. Задана функція і два значення аргументу і . Необхідно:

1. Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;

2. У випадку розриву знайти її односторонні границі в точках розриву;

3. Зробити схематичний рисунок.

Розв’язання. Проведемо дослідження функції на неперервність в точках та , для чого знайдемо односторонні границі.

В точці маємо ,

,

.

Отже, в даній точці і функція в точці є неперервною.

В точці маємо , тобто в дані точці функція невизначена. Далі

,

.

Таким чином, в точці функція має розрив другого роду. Дослідимо поведінку функції коли :

,

.

Отже, пряма є горизонтальною асимптотою графіка функції . Схематичний графік функції наведено на рисунку 5.

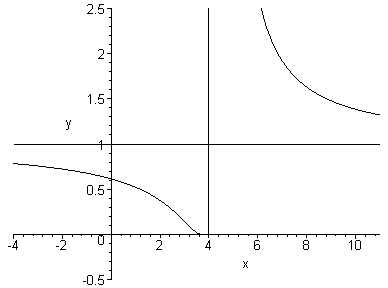
Рис. 5.

Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.

Розв’язання. Функції , неперервні на всій числовій вісі, функція неперервна на проміжку . Отже, задана функція може мати розриви тільки в точках, де змінюється її аналітичний вираз, тобто в точках і . Проведемо дослідження функції на неперервність в цих точках, для чого знайдемо відповідні односторонні границі і значення функції.

В точці маємо:

, , .

Таким чином, в даній точці

,

Тобто функція має розрив 1-го роду і неперервна зліва. Стрибок функції в точці дорівнює 1.

Аналогічно, в точці маємо:

, , .

Таким чином, в даній точці

,

тобто, функція в точці функція неперервна.

Схематичний графік функції наведено на рисунку 6.

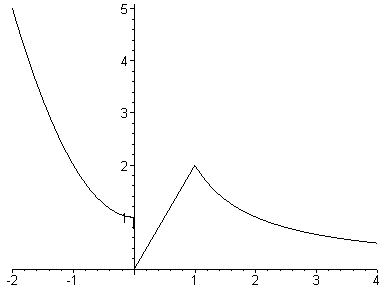
Рис. 6.