
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДНІПРОДЗЕРЖИНСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
МЕТОДИЧНІ ВКАЗІВКИ
до самостійної роботи з дисципліни
«Математичний аналіз»
(змістовий модуль 1)
для студентів, що навчаються за напрямом
6.040301 “Прикладна математика”
ЗАТВЕРДЖЕНО:
Редакційно-видавничою секцією
науково-методичної ради ДДТУ
“ _____ ” _____ 2011 р. протокол №
Дніпродзержинськ
2011
Розповсюдження і тиражування без офіційного дозволу Дніпродзержинського державного технічного університету заборонено.
Методичні вказівки до самостійної роботи з дисципліни «Математичний аналіз» для студентів, що навчаються за напрямом 6.040301 “Прикладна математика” (змістовий модуль 1) / Укладач С.В.Тимченко – Дніпродзержинськ, ДДТУ, 2011. - 46 с.
Укладач: С.В.Тимченко, ст. викладач
Відповідальний за випуск: С.Є.Самохвалов,
проф., доктор техн. наук
Рецензент: В.В.Кармазіна, к.ф.-м.наук, доцент
Затверджено на засіданні кафедри ПМ
протокол № 12 від 31.05.2011 р.
Коротка анотація до видання. У методичних вказівках до самостійної роботи студентів з дисципліни “Математичний аналіз” (змістовий модуль 1) надано варіанти індивідуальних завдань для модульного контролю. Наведено зразок виконання індивідуального завдання.
ЗМІСТ
Вступ . . . . . . . . . . . . . . . . . . . . . . . . . . 4 |
Варіант 1 . . . . . . . . . . . . . . . . . . . . . . . . . . 5 |
Варіант 2 . . . . . . . . . . . . . . . . . . . . . . . . . . 6 |
Варіант 3 . . . . . . . . . . . . . . . . . . . . . . . . . . 7 |
Варіант 4 . . . . . . . . . . . . . . . . . . . . . . . . . . 9 |
Варіант 5 . . . . . . . . . . . . . . . . . . . . . . . . . . 10 |
Варіант 6 . . . . . . . . . . . . . . . . . . . . . . . . . . 11 |
Варіант 7 . . . . . . . . . . . . . . . . . . . . . . . . . . 13 |
Варіант 8 . . . . . . . . . . . . . . . . . . . . . . . . . . 14 |
Варіант 9 . . . . . . . . . . . . . . . . . . . . . . . . . . 15 |
Варіант 10 . . . . . . . . . . . . . . . . . . . . . . . . . 17 |
Варіант 11 . . . . . . . . . . . . . . . . . . . . . . . . . 18 |
Варіант 12 . . . . . . . . . . . . . . . . . . . . . . . . . 19 |
Варіант 13 . . . . . . . . . . . . . . . . . . . . . . . . . 21 |
Варіант 14 . . . . . . . . . . . . . . . . . . . . . . . . . 22 |
Варіант 15 . . . . . . . . . . . . . . . . . . . . . . . . . 23 |
Варіант 16 . . . . . . . . . . . . . . . . . . . . . . . . . 25 |
Варіант 17 . . . . . . . . . . . . . . . . . . . . . . . . . 26 |
Варіант 18 . . . . . . . . . . . . . . . . . . . . . . . . . 27 |
Варіант 19 . . . . . . . . . . . . . . . . . . . . . . . . . 29 |
Варіант 20 . . . . . . . . . . . . . . . . . . . . . . . . . 30 |
Зразок виконання індивідуального завдання . . . . . . 31 |
Перелік літератури . . . . . . . . . . . . . . . . . . . . 46 |
ВСТУП
Важливим елементом засвоєння математики й оволодіння її методами є самостійна робота студентів. Ця робота є неперервною складовою виконання поточних домашніх завдань і циклічної роботи з виконання індивідуальних модульних завдань. Результативність самостійної роботи студентів забезпечується ефективною системою контролю, яка включає опитування студентів за змістом лекції, перевірку виконання поточних домашніх завдань, розв’язування задач біля дошки, захист індивідуальних модульних робіт.
Метою індивідуальних домашніх завдань є перевірка результативності самостійної роботи з даного модуля.
Студент повинен самостійно розв’язати індивідуальні домашні завдання свого варіанта, який відповідає номеру студента у списку навчальної групи.
Розв’язання завдань із поясненнями слід подати у зошиті, на обкладинці якого необхідно написати назву дисципліни та модуля; прізвище студента, його ім’я і по батькові; курс, номер групи; номер варіанта. Кожне завдання необхідно позначати його номером за методичними вказівками. Умову завдання треба переписати повністю.
Якщо після перевірки роботи викладачем зроблені зауваження, студент повинен розв’язати наново неправильно виконані завдання у тому самому зошиті і повторно подати його на перевірку. Після позитивної оцінки викладача робота підлягає захисту.
ВАРІАНТ 1
Завдання
1.
Довести, що
![]() (знайти номер
(знайти номер
![]() ):
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() , б)
, б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ;
в)
;
в)
![]() ;
б)
;
б)
![]() ;
г)
;
г)
![]() .
.
Завдання
4.
Довести (знайти
![]() ), що:
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() , б)
, б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() , д)
, д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
![]() ),
що функція
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і два значення аргументу
![]() і
і
![]() .
Необхідно:
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8.
Функція
![]() задана різними аналітичними виразами
для різних областей зміни незалежної
змінної. Знайти точки розриву функції,
якщо вони існують. Зробити рисунок.
задана різними аналітичними виразами
для різних областей зміни незалежної
змінної. Знайти точки розриву функції,
якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 2
Завдання
1.
Довести, що
![]() (знайти номер
):
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ;
в)
;
в)
![]() ;
б)
;
б)
![]() ;
г)
;
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() , е)
, е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і два значення аргументу
![]() і
і
![]() .
Необхідно:
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 3
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ;
в)
;
в)
![]() ;
б)
;
б)
![]() ;
г)
;
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() , б)
, б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 4
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
),
що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() , б)
, б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і два значення аргументу![]() і
і
![]() .
Необхідно:
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 5
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
),
що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція![]() і два значення аргументу
і два значення аргументу
![]() і
.
Необхідно:
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 6
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
і два значення аргументу
і
![]() .
Необхідно:
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 7
Завдання
1.
Довести, що
(знайти номер
):![]() ,
,![]()
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
),
що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() , б)
, б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
.
неперервна в точці
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і два значення аргументу
![]() і
.
Необхідно:
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 8
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() , б)
, б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і два значення аргументу
![]() і
і
![]() .
Необхідно:
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 9
Завдання
1.
Довести, що
(знайти
номер
):![]() ,
,
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() , г)
, г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() , б)
, б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
 .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
.
неперервна в точці
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і два значення аргументу
![]() і
і
![]() .
Необхідно:
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 10
Завдання
1.
Довести, що
(знайти номер
):![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що: ![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() , е)
, е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і два значення аргументу
![]() і
і
![]() .
Необхідно:
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 11
Завдання
1.
Довести, що
(знайти номер
):![]() ,
.
,
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() , г)
, г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 12
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
 ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
.
,
г)
.
Завдання
4.
Довести (знайти
), що: ![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() , е)
, е)
 .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 13
Завдання
1.
Довести,
що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() , е)
, е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 14
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() , е)
, е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 15
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() , е)
, е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
неперервна в точці
![]() .
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 16
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() , е)
, е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
.
неперервна в точці
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 17
Завдання
1.
Довести, що
(знайти номер
):![]() ,
,![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() , е)
, е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
.
неперервна в точці
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і два значення аргументу![]() і
.
Необхідно:
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 18
Завдання
1.
Довести,
що
(знайти номер
):
![]() ,
,
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
.
неперервна в точці
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 19
Завдання
1.
Довести,
що
(знайти номер
):
![]() ,
.
,
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() , д)
, д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
.
неперервна в точці
.
Завдання
7.
Задана функція
![]() і два значення аргументу
і
.
Необхідно:
і два значення аргументу
і
.
Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
ВАРІАНТ 20
Завдання
1.
Довести,
що
(знайти номер
):
![]() ,
.
,
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Завдання
4.
Довести (знайти
), що:
![]() .
.
Завдання 5. Обчислити границі функцій:
а)
![]() ,
б)
,
б)
![]() , в)
, в)
![]() ,
,
г)
![]() ,
д)
,
д)
![]() ,
е)
,
е)
![]() .
.
Завдання
6. Довести
(знайти
),
що функція
![]() неперервна в точці
.
неперервна в точці
.
Завдання 7. Задана функція і два значення аргументу і . Необхідно:
Встановити, чи буде дана функція неперервною чи розривною для кожного із заданих значень аргументу;
У випадку розриву знайти її односторонні границі в точках розриву;
Зробити схематичний рисунок.
Завдання 8. Функція задана різними аналітичними виразами для різних областей зміни незалежної змінної. Знайти точки розриву функції, якщо вони існують. Зробити рисунок.
![]()
Зразок виконання індивідуального завдання
Завдання
1.
Довести, що
(знайти номер
):
![]() ,
.
,
.
Розв’язання.
Виберемо
довільне число
![]() .
Тоді
.
Тоді
![]() .
.
Нерівність
![]() буде виконуватися в точності тоді, коли
буде виконуватися в точності тоді, коли
![]() ,
тобто
,
тобто
![]() ,
звідки
,
звідки
![]() .
.
Покладемо
![]() ,
отримаємо, що для всіх
,
отримаємо, що для всіх
![]() справедлива нерівність
справедлива нерівність
![]() .
Відповідно до означення границі, маємо
що
.
Відповідно до означення границі, маємо
що
![]() .
.
Завдання 2. Обчислити границі числових послідовностей:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
.
Розв’язання.
а)
Маємо невизначеність
![]() .
Перетворимо окремо вираз чисельника
та знаменника:
.
Перетворимо окремо вираз чисельника
та знаменника:
![]()
![]() ;
;
![]() .
.
Тоді границя набуває вигляду:
![]() .
.
Поділимо
чисельник та знаменник на старшу степінь
n,
тобто на
![]() :
:
 .
.
В
останній рівності ми використали той
факт, що послідовність
![]() є нескінченно малою.
є нескінченно малою.
Таким
чином,
![]() .
.
б) Маємо невизначеність .
 .
.
Враховуємо,
що послідовності
![]() і
і
![]() - нескінченно малі. Поділимо чисельник
та знаменник на старшу степінь n,
тобто на
:
- нескінченно малі. Поділимо чисельник
та знаменник на старшу степінь n,
тобто на
:
 .
.
Отже,
![]() .
.
в) Сума, що стоїть в чисельнику є сумою арифметичної прогресії, тоді
![]() .
.
Таким чином,
![]()
 .
.
г)
Маємо невизначеність виду
![]() .
Для її розкриття перетворимо вираз в
дужках
.
Для її розкриття перетворимо вираз в
дужках
![]()
![]() .
.
Отже,
![]() .
.
Зводимо отриману границю до другої стандартної границі
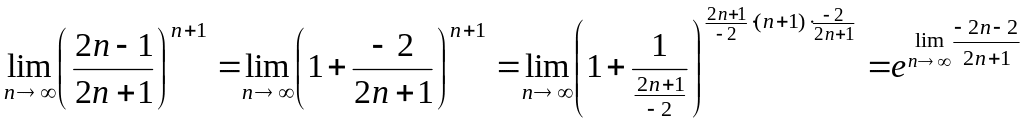 .
.
Обчислимо границю, що присутня в степені
 ,
,
тоді
![]() .
.
д)
маємо невизначеність
![]() .
Помножимо та поділимо вираз під знаком
границі на спряжене до нього, після чого
скористуємося формулою різниці квадратів.
.
Помножимо та поділимо вираз під знаком
границі на спряжене до нього, після чого
скористуємося формулою різниці квадратів.

 .
.
Тому
![]()
 .
.
Враховуємо,
що послідовності
![]() і
і
![]() - нескінченно малі, а послідовність
- нескінченно малі, а послідовність
![]() - нескінченно велика, Отже,
- нескінченно велика, Отже,
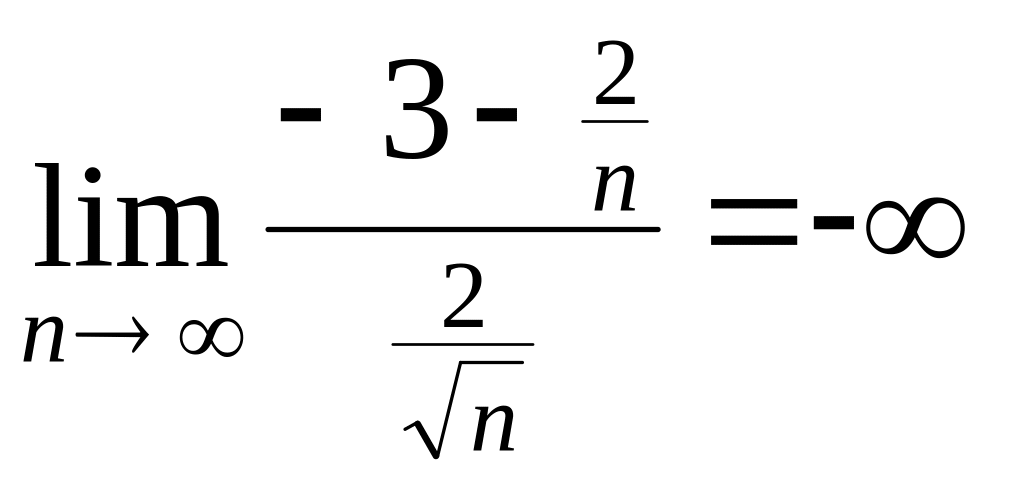 ,
а значить і
,
а значить і
![]() .
.
Завдання 3. Побудувати графіки заданих функцій:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
.
;
г)
.
Зауваження. На рисунка точками позначено графік початкової функції, лінією – графік шуканої функції.
Розв’язання.
а) .
Перетворимо задане рівняння наступним чином (виділяємо повний квадрат):
![]() .
.
Отже,
щоб отримати графік заданої функції
необхідно вершину параболи
![]() перенести у точку (-2; -2) (рис.1).
перенести у точку (-2; -2) (рис.1).
б) .
Виконуємо перетворення заданого рівняння:
![]() .
.
Таким
чином, графік функції
![]() необхідно перенести праворуч на 2
одиниці, стиснути уздовж осі Ох
у 2 рази та перенести на 6 одиниць вниз
(рис.2).
необхідно перенести праворуч на 2
одиниці, стиснути уздовж осі Ох
у 2 рази та перенести на 6 одиниць вниз
(рис.2).
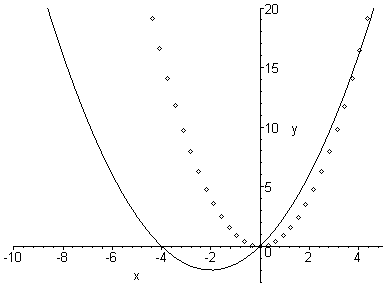

Рис.1. Рис.2.
в) .
Виконуємо перетворення заданого рівняння наступним чином:
![]() .
.
Отже,
графік початкової функції
![]() необхідно перенести праворуч та вгору
на 2 одиниці (рис.3).
необхідно перенести праворуч та вгору
на 2 одиниці (рис.3).
г) .
Перетворимо задане рівняння наступним чином:
![]() .
.
Отже,
графік початкової функції
![]() необхідно перенести на
необхідно перенести на
![]() одиниць праворуч, стиснути у 3 рази
уздовж осі Ох,
дзеркально відобразити відносно осі
Ох та перенести на ½ одиниць вниз (рис.4).
одиниць праворуч, стиснути у 3 рази
уздовж осі Ох,
дзеркально відобразити відносно осі
Ох та перенести на ½ одиниць вниз (рис.4).
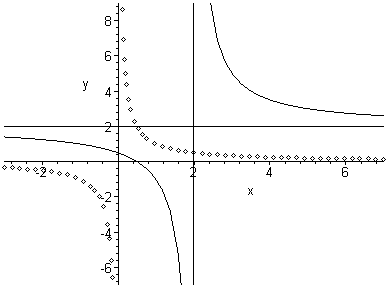
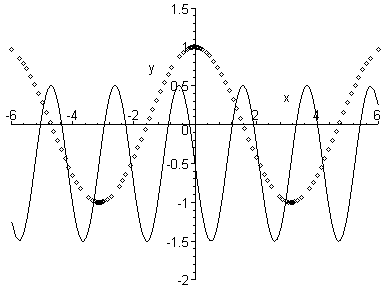
Рис.3. Рис.4.
Завдання
4.
Довести (знайти
), що
![]() .
.
Розв’язання.
Зафіксуємо довільне число
.
Необхідно за цим ε
знайти таке число
![]() ,
щоб з умови
,
щоб з умови
![]() ,
тобто
,
тобто
![]() виходила нерівність
виходила нерівність
![]() ,
тобто
,
тобто
![]() .
Останню нерівність перепишемо наступним
чином
.
Останню нерівність перепишемо наступним
чином
![]() .
.
Маємо
![]() ,
, ![]() ,
,
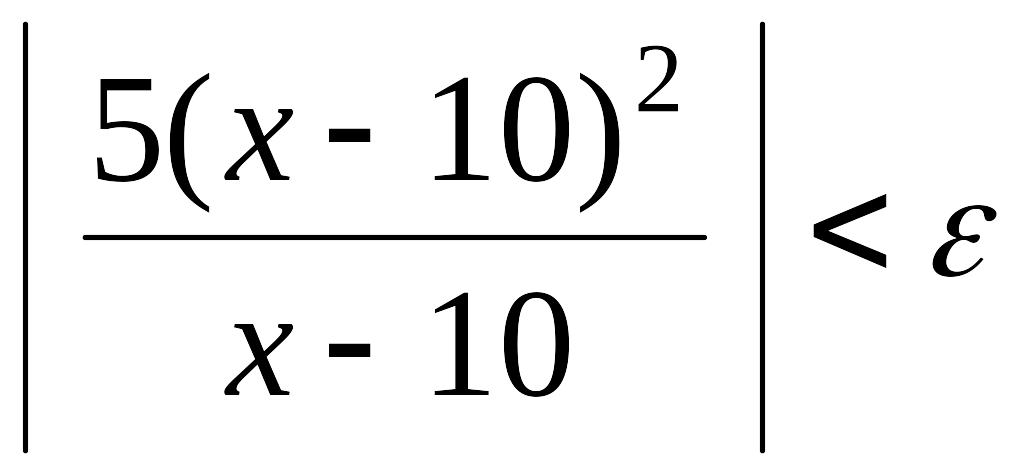 ,
, ![]() .
.
Звідси
виходить, що, якщо взяти
![]() ,
то нерівність
,
то нерівність
![]() буде автоматично тягнути за собою
нерівність
,
тобто для всіх х,
для яких виконується перша нерівність
буде виконуватися і друга. За означенням
границі маємо, що
.
буде автоматично тягнути за собою
нерівність
,
тобто для всіх х,
для яких виконується перша нерівність
буде виконуватися і друга. За означенням
границі маємо, що
.
Завдання 5. Обчислити границі функцій:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
.
