3.7. Оценка качества воды с использованием  -метода проверки статистических гипотез

Раздел подготовлен в соавторстве с д-ром Натаном Цейтлиным (Геттинген, Германия) и на основе материалов его книги "Из опыта аналитического статистика" [http://matstat.gmxhome.de].

Методики, описанные в предыдущих разделах, основаны на предположении, что заранее известны точные (т.е. истинные) значения C₁, C₂ ,..., C_n концентраций вредных веществ в воде изучаемого водоема. В реальных условиях исследователь имеет дело с некоторой эмпирической выборкой значений C_i, j =  , из стохастического временного ряда наблюдений, имеющего принципиально вероятностную природу вследствие нестационарного воздействия антропогенных факторов и погрешности измерений.

Пусть (С₁, С_2,…, С_n)^Т - случайный вектор концентраций примесей в воде, элементы которого независимы и измеряются со случайными погрешностями. Концентрация каждого j-го компонента (j =  ) имеет нормальный закон распределения с математическим ожиданием M{С_j} и дисперсией D{С_j }.

Предположим, что мы располагаем представительными выборками   объемом по N_j значений результатов параллельных измерений концентрации вредных веществ, что позволяет получить оценки параметров - математических ожиданий   и среднеквадратических отклонений   для распределений соответствующих случайных величин С_j :

,  , (3.10)

где f_j = N_j -1 - число степеней свободы величины S_j (j = ).

Рассмотрим возможные подходы к комплексной оценке качества воды. Согласно СанПиН 2.1.5.980-00 “при обнаружении в воде химических веществ с одинаковыми лимитирующими признаками вредности, сумма отношений обнаруженных концентраций к их ПДК:

  (3.11)

не должна быть более единицы”. Использование формулы (3.11) предполагает две оценки качества воды - “безвредная” (при μ < 1) и “вредная” (при μ > 1).

Поскольку концентрации загрязняющих компонентов С_i представляют собой случайные величины, то и критерии качества воды на их основе также носят вероятностный характер. Следовательно, для оценки качества воды необходимо воспользоваться теорией проверки статистических гипотез [Леман, 1964].

Статистическая оценка математического ожидания показателя μ загрязнения воды примесями может быть вычислена по формуле (3.11), куда вместо параметров С_j подставляются их соответствующие оценки  :

,  (3.12)

а ПДК каждой примеси являются действительными (неслучайными) числами.

Оценка   дисперсии D{μ} и дисперсия   ошибки оценки m показателя качества μ выражаются формулами

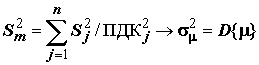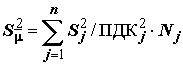 и  .  (3.13)

Формально задача ставится следующим образом. Необходимо оценить качество воды путем проверки двух гипотез Н_А: μ < 1 (безвредная) против Н_В: μ > 1 (вредная), для чего воспользуемся последовательностью действий, определяемой теорией [Леман, 1964] и практикой [Цейтлин, 1984] проверки статистических гипотез.

1. В качестве статистической характеристики гипотезы выбирается распределение Стьюдента t_f с f степенями свободы при малых значениях f (1 ≤ f ≤ 25) и нормированное нормальное распределение Z при больших значениях f (f > 25).

2. В качестве нулевой Н₀ гипотезы формулируется то предположение, ошибочное отклонение которого дает наибольший ущерб. Например, с точки зрения экосистемы водоема ошибочное отклонение гипотезы Н_В, когда она верна, приводит к более тяжелым последствиям, чем ошибочное отклонение Н_А, когда она верна. Исходя из этого, формулируем

Н₀ = Н_В : μ ≥ 1 против альтернативы Н₁ = Н_А : μ < 1.   (3.15)

3. Задается критические значения уровня значимости α_к из рекомендованных в работе [Цейтлин, 1984] интервалов: 0,3 ≤ α_к ≤ 1, когда ответственность за выводы предельно малая, 0,1 ≤ α_к < 0,3 - малая; 0,03 ≤ α_к < 0,1 - обычная; 0,001<α_к<0,03 - большая; 0 < α_к < 0,001 - предельно большая.

4. Выполняются необходимые эксперименты, имеющие цель получить представительные выборки   объемом по N_j значений величин С_j (i = ) результатов параллельных измерений концентрации загрязняющих веществ.

5. Вычисляется оценка   уровня значимости α (α - вероятность ошибочного отклонения проверяемой гипотезы Н₀, если она верна):

,   (3.16)

где Z_α = L- [L²-2t_f,α•(f + 3)]^0,5, L = f +1.5 t_f,α+3; t_f,α - верхний α-предел распределения Стьюдента (t_f,α > 1) с f степенями свободы, число которых может быть определено по формуле Уэлча [Браунли, 1977]: .  (3.17)

Если рассматривается гипотеза Н₀ = Н_B, то значения t_f,α вычисляются как

 .  (3.18)

6. Принимается решения о проверяемой гипотезе. Условия отклонения нулевой гипотезы   ≤ α_к. Если же   > α_к , то гипотезу Н₀ не отклоняют.

Формулировка нулевой гипотезы Н₀ в виде (3.15) отражает точку зрения “Водопользователя” (ВП), т.е. населения, использующего воду в хозяйственных или питьевых целях, а также сообществ гидробионтов, населяющих водоем, активистов движения “Green Peace” и проч. С позиций ВП ошибочное отклонение гипотезы о плохом качестве воды может привести к тяжелым последствиям для экосистемы и здоровья человека и, с учетом этого риска, критическое значение α_к выбирается из большого или предельно большого уровня ответственности, например,α_кВП = 0.01.

Однако, представляется целесообразным учесть и экономические интересы “Водоочистителя” (ВО) – организации, ответственной за очистку сбрасываемых в водоем сточных вод до нормативного качества, а также другого производителя, лимитирующего свою хозяйственную деятельность в соответствии с требованиями водоохранных органов. Для ВО ошибочное отклонение гипотезы о чистоте воды (Н_А), когда она верна, приводит к более тяжким экономическим последствиям, чем ошибочное отклонение Н_B, если она справедлива (см. табл. 3.20). Поэтому ВО формулирует нулевую гипотезу следующим образом:

Н₀ = Н_А: μ ≤ 1 против Н₁ = Н_B: μ > 1,  (3.19)

а верхний α-предел распределения Стьюдента вычисляется по формуле:

.  (3.20)

Для принятия решения о проверяемой гипотезе для ВО могут быть выбраны более "мягкие" уровни ответственности за выводы, например, при критических значениях α_кВ0 = 0.1.

Области (0 <   ≤ α_кi) (i   [ВО; ВП]) отклонения нулевой гипотезы называются критическими. Их взаимно однозначное отображение на область значений показателя μ загрязнения водоема происходит по-разному, в зависимости от сформулированных нулевой и альтернативной гипотез, отражающих интересы субъектов с различной точкой зрения (см. рис. 3.2.).

Для ВО критической областью является (μ: μ_кВО< μ < ∞); для ВП - это (μ: 0 < μ < μ_кВП). Поскольку уравнение (3.16) легко выразить явно относительно t_f,α , то критические значения меры μможно найти [Дубницкий, Цейтлин, 1999], подставив в формулы (3.18) и (3.20) критические значения уровней значимости α_кВ0 и α_кВП соответственно, и решая их относительно  :

μ_кВО = 1 +  ; α = α_кВ0; (3.21)

μ_кВП = 1 -  ; α = α_кВП. (3.22)

На рис. 3.2 представлены функции распределения оценки   величины μ в предположении о справедливости гипотезы Н₀, сформулированной с точки зрения “Водоочистителя” F(μ) и “Водопользователя” P( < μ). Очевидно, что P(μ) = 1- F(μ).

Таблица 3.20

Распределение результатов решений при проверке гипотез о соответствии качества воды установленным нормам

Предполагается	Позиция лица, принимающего решение (ЛПР)	Результат решения в зависимости от истинности гипотезы
		НА:  <1 (безвредная вода)	НВ :  >1 (вредная вода)
Отклонить НВ:  >1 (вода безвредная)	Станция очистки воды (ВО)	Верно: получает плату за безвредную воду	Ошибка: получает плату за безвредную воду, хотя она вредная
	Потребитель воды (ВП)	Верно: платит за безвредную воду	Ошибка: платит за безвредную воду, но отравляется вредной водой
Отклонить НА:  <1 (вода вредная)	Станция очистки воды (ВО)	Ошибка: лишние затраты на очистку или (и) штраф	Верно: необходимы затраты на очистку или (и) штраф
	Потребитель воды (ВП)	Ошибка: лишние затраты, вызванные ограничением потребления воды	Верно: необходимы затраты, вызванные ограничением потребления воды

 

Рис. 3.2. Отображение критических областей оценки уровня значимости   (0 <   ≤ α_кi) показателя качества воды μ для лиц, принимающих решения в интересах “Водоочистителя” (а) и “Водопользователя” (б)

Среди множества решений о качестве воды существует область (μ_кВП< <μ_кВО), в которой могут встретиться спорные решения, т.е. “Водоочиститель” оценивает качество воды какбезвредное, а “Водопользователь” – как вредное. Один из способов разрешения такого "спора" заключается в увеличении объемов N_j выборок: согласно формуле (3.13) среднеквадратичное отклонение S_μ новой оценки μ с ростом N_j уменьшается; а спорная область при неизменных α_кВ0 и α_кВП сужается. Менее трудоемким способом выхода из спорной области может быть пересмотр обоими субъектами критических уровней значимости α_кi: при их увеличении принимается меньший уровень ответственности за выводы (чем больше α_кi, тем значения t_f,α в формулах (3.21) и (3.22) меньше).

Изложенный подход формализации задачи остается, в основном, без изменений и при других способах комплексной оценки качества воды, описанных в разделе 3.4. В алгоритм необходимо лишь внести коррективы, учитывающие особенности расчетной формулы выбранного показателя, отличного от (3.11). Например, примем более мягкие условия нормирования качества: вода считается "чистой", если каждая из анализируемых примесей C_i, j =  , не более нормируемой величины ПДК_i то есть, для всех j справедливо C_i,/ ПДК_i < 1. Тогда исходные гипотезы примут вид: Н_{А j}: С_j < ПДК_j (безвредная) против Н_Вj : С_j > ПДК_j (вредная).