Глава 2 Плоскость в пространстве
§1 Различные виды уравнения плоскости
Каждая плоскость
в пространстве
определяется линейным алгебраическим
уравнением
первой степени.
1 Общее уравнение плоскости:
(17)
2 Уравнение
плоскости, проходящей через точку
перпендикулярно вектору
:
(18)
Всякий ненулевой
вектор, перпендикулярный данной
плоскости, называется нормальным
вектором этой плоскости. В частности,
вектор
- нормальный вектор плоскости.
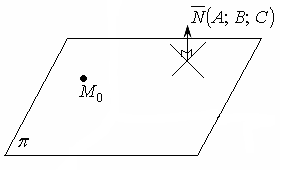
Рисунок 30
Частные случаи уравнения (17):
- плоскость проходит
через начало координат;
- плоскость
параллельна оси
(аналогичный смысл
имеют уравнения
);
- плоскость проходит
через ось
(
,
- через ось
и
соответственно);
(
)
– плоскость параллельна плоскости
(
,
- параллельно плоскости
и
соответственно);
,
т.е.
- плоскость совпадает с плоскостью
(
,
- уравнения плоскостей
и
соответственно).
3 Уравнение
плоскости в отрезках:
,
где
- абсцисса, ордината и аппликата точек
пересечения плоскостью
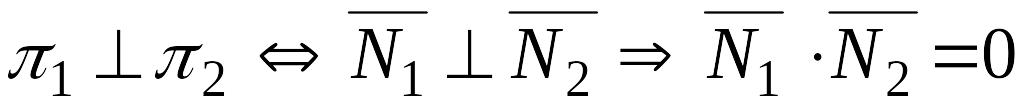
Рисунок 31
4 Уравнение
плоскости, проходящей через три различные
точки
,
и
:
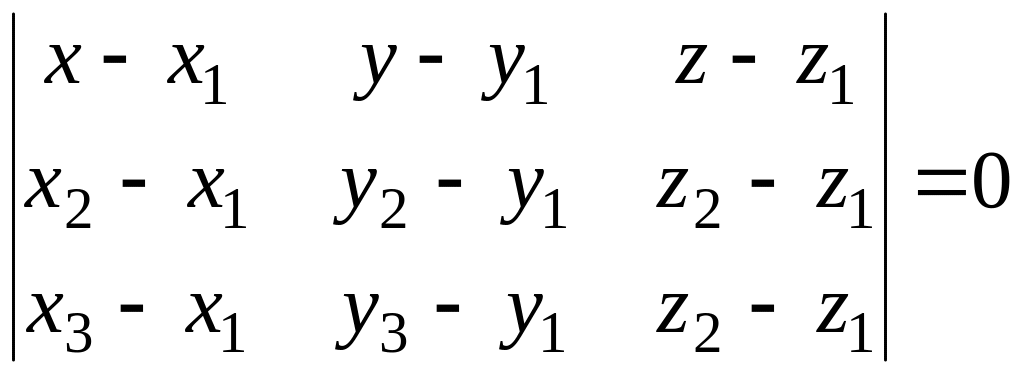(19)
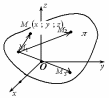
Рисунок 32
5 Нормальное уравнение плоскости:
(20)
где
- длина перпендикуляра
,
опущенного из начала координат на
плоскость;
- углы, образованные единичным вектором
,
имеющего направление перпендикуляра
(рисунок 33), с осями
,
и
(
).
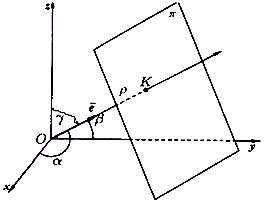
Рисунок 33
Общее уравнение плоскости (17) приводится к нормальному виду (20) путем умножения на нормирующий множитель
;
знак перед дробью
берется противоположный знаку свободного
члена
(в общем уравнении плоскости).
§2 Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей. Расстояние от данной точки до данной плоскости
Углом между
плоскостями в пространстве называется
угол между нормальными векторами этих
плоскостей. Две плоскости
и
заданы уравнениями
и
,
где
,
.
Наименьший из двух смежных углов, образованных этими плоскостями, находится по формуле:
(21)
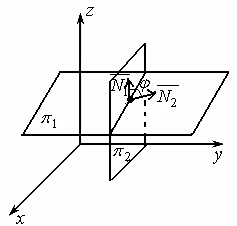
Рисунок 34
Условие параллельности плоскостей:
Д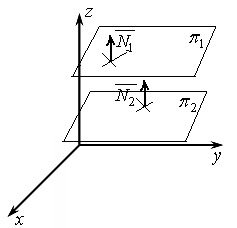
ве
плоскости параллельны
тогда и только
тогда, когда их нормальные вектора
коллинеарны,
т.е.
(22)
Рисунок 35
Условие перпендикулярности плоскостей:
Две плоскости перпендикулярны тогда и только тогда, когда их нормальные вектора перпендикулярны, т.е.
(23)
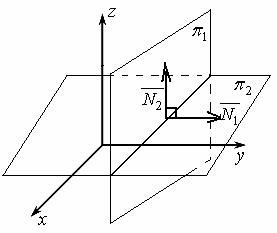
Рисунок 36
Условие совпадения
двух плоскостей
:
(24)
Рисунок 37
Расстояние
от точки
до плоскости
находится по формуле
(25)
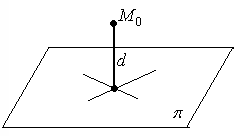
Рисунок 38
Если плоскость
задана уравнением
,
то расстояние от точки
до плоскости может быть найдено по
формуле
(26)