
- •Глава 4.
- •Глава 6.
- •Глава 9.
- •Глава 10.
- •Глава 11.
- •Глава 12.
- •Глава 13.
- •Глава 14.
- •Глава 15.
- •Глава 16
- •Глава 18
- •Глава 1.
- •§ 1. Аксиомы и принципы статики твёрдого тела.
- •§ 2. Момент силы относительно произвольного центра, оси.
- •§ 3. Пара сил и её свойства.
- •§ 4.Главный вектор и главный момент системы сил. Правило Пуансо.
- •§ 5. Приведение системы сил к простейшему виду.
- •§ 6. Уравнения равновесия тела.
- •Глава 2. Центр параллельных сил и центр тяжести.
- •§ 1. Центр параллельных сил.
- •§ 2. Центр тяжести, методы определения координат центра тяжести.
- •Глава 3. Равновесие при наличии сил трения.
- •§ 1. Трение скольжения Угол трения, конус трения.
- •§ 2. Задача об опрокидывании тела. Трение качения.
- •Кинематика
- •Глава 4. Кинематика точки.
- •§ 1. Способы задания движения точки. Уравнения движения точки; траектория.
- •§ 2. Натуральный триэдр траектории.
- •§ 3. Скорость точки.
- •§ 4. Ускорение точки.
- •§ 5. Поступательное движение твердого тела.
- •Глава 5. Вращение твердого тела вокруг неподвижной оси.
- •§ 1 Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси.
- •§ 2. Векторные формулы скорости и ускорения точек тела, вращающегося вокруг неподвижной оси.
- •Глава 6. Кинематика плоского движения твердого тела
- •§ 1. Уравнения плоского движения.
- •§ 2. Скорости точек плоской фигуры.
- •§ 3. Мгновенный центр скоростей плоской фигуры.
- •§ 4. Ускорения точек плоской фигуры.
- •Глава 4. Вращение тела вокруг неподвижной точки. Общий случай движения тела.
- •§ 1. Определение положения твердого тела, имеющего неподвижную точку.
- •§ 2 Углы Эйлера, матрицы поворота.
- •§ 3. Угловая скорость и угловое ускорение твердого тела, имеющего неподвижную точку.
- •§ 4. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижного центра.
- •Глава 6.
- •§ 5. Определение положения твердого тела в пространстве.
- •§ 6. Скорости и ускорения в общем случае движения твердого тела.
- •Глава 8. .Кинематика относительного движения точки и тела.
- •§ 1. Абсолютное, относительное и переносное движения.
- •§ 2. Теорема о сложении скоростей в относительном движении.
- •§ 3. Сложение ускорений, теорема Кориолиса.
- •§ 4. Сложение вращений твёрдого тела.
- •§ 5. Общий случай движения тела (для скоростей).
- •Динамика точки и твёрдого тела
- •Глава 9. Динамика точки.
- •§ 1. Основные положения и аксиомы динамики
- •§ 2. Дифференциальные уравнения движения материальной точки.
- •§ 3. Динамики относительного движения точки.
- •Глава 10. Количество движения системы.
- •§ 1. Уравнения динамики системы материальных точек и твёрдого тела.
- •§ 2. Теорема об изменении количества движения системы материальных точек.
- •§ 3. Теорема о движении центра масс.
- •Глава 11. Кинетический момент системы и твёрдого тела.
- •§ 1. Теорема об изменении главного момента количества движения системы материальных точек.
- •§ 3. Кинетический момент тела, вращающегося относительно неподвижной точки.
- •§ 3. Момент инерции относительно произвольной оси. Тензор инерции.
- •§ 4. Главные оси инерции и главные моменты инерции.
- •§ 5. Вычисление моментов инерции.
- •§ 6. Преобразование моментов инерции.
- •§ 7. Кинетический момент твердого тела.
- •Глава 12. Дифференциальные уравнения движения твердого тела.
- •§ 1. Дифференциальные уравнения вращения твердого тела.
- •§ 2. Общий случай движения твердого тела.
- •§ 3. Динамика плоско-параллельного движения тела.
- •§ 4. Реакция оси вращающегося тела.
- •§ 5. Задача о физическом маятнике.
- •Глава 13. Кинетическая энергия системы и твёрдого тела.
- •§ 1. Кинетическая энергия системы материальных точек.
- •§ 2. Кинетическая энергия твердого тела.
- •§ 3. Работа силы. Мощность.
- •§ 4. Примеры вычисления потенциальной энергии и работы
- •§ 5. Теорема об изменении кинетической энергии.
- •§ 6. Закон сохранения механической энергии.
- •Динамика несвободной системы. __________________________________________________________Глава 14. Возможные перемещения.
- •§1. Связи, классификация связей, число степеней свободы.
- •§2. Возможные перемещения.
- •§ 3. Принцип освобождаемости. Идеальные связи.
- •§ 4. Статический принцип возможных перемещений.
- •§ 5. Динамический принцип возможных перемещений. Общее уравнение динамики.
- •Глава 15. Уравнение Лагранжа второго рода и его приложения.
- •§ 1. Вывод уравнения Лагранжа второго рода.
- •§ 2. Диссипативная функция.
- •§ 8. Представление кинетической энергии как функции обобщённых скоростей.
- •§ 9. Интеграл энергии.
- •Малые колебания системы с одной степенью свободы.
- •Глава 16 Свободные колебания системы с одной степенью свободы.
- •§ 1. Устойчивость равновесия голономной системы в консервативном силовом поле.
- •§ 2. Малые свободные колебания системы с одной степенью свободы.
- •§ 3. Свободные колебания системы с учётом линейно-вязкого сопротивления.
- •Глава 17.
- •§ 1. Вынужденные колебания без сопротивления. Биения, резонанс.
- •§ 2. Вынужденные колебания системы с учётом линейно-вязкого трения.
- •§ 3. Динамические характеристики вынужденных колебаний.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Глава 18 Уравнения статики деформируемого твёрдого тела.
- •§ 1. Дифференциальные уравнения равновесия нерастяжимой нити.
- •§ 2. Статика деформируемых прямых стержней.
- •Глава 19. Элементарная теория удара
- •§ 1. Теорема импульсов и её приложения в теории удара.
- •§ 2. Задача Герца о прямом и центральном ударе двух тел.
- •§ 3. Теоремы об изменении количества движения и кинетического момента при ударе.
- •§ 4. Удар, действующий на тело, вращающегося вокруг неподвижной оси.
- •§ 5. Условия отсутствия ударных реакций. Центр удара.
- •1.Статика.
- •2. Кинематика.
- •3. Динамика точки и твердого тела:
- •4. Динамика несвободной системы.
- •5. Колебания системы около положения устойчивого равновесия.
- •Дополнительные вопросы, включаемые по согласованию с выпускающими кафедрами: Динамические характеристики вынужденных колебаний. Нелинейные колебания точки. Метод Ван дер Поля.
- •3. Теорема о движении центра масс.
- •6. Теорема об изменении кинетической энергии.
Некоторые задачи статики и динамики точки и твёрдого тела.
Предлагаемые приложения не входят в обязательные главы курса теоретической механики, но представляют, по мнению автора, определённый интерес. Ниже будет показано, что для деформируемых тел выполняются те же необходимые и достаточные условия равновесия – равенство нулю главного вектора и главного момента приложенных сил, но сами уравнения равновесия имеют вид дифференциальных зависимостей.
Глава 18 Уравнения статики деформируемого твёрдого тела.
§ 1. Дифференциальные уравнения равновесия нерастяжимой нити.
Задана
невесомая нить длиной ds,
(рис.65 ), нагруженная распределённой
нагрузкой
![]() .
Нить абсолютно гибкая и нерастяжимая.
В данных предположениях достаточно
записать уравнения равновесия в виде
,
главный вектор всех сил равен нулю.
.
Нить абсолютно гибкая и нерастяжимая.
В данных предположениях достаточно
записать уравнения равновесия в виде
,
главный вектор всех сил равен нулю.

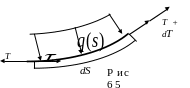
Раскроем полученное выражение
![]() .
.
Первые
два слагаемых сокращаются, произведением
![]() можно
пренебречь, как величиной второго
порядка, остаются только
можно
пренебречь, как величиной второго
порядка, остаются только
![]() .
Разделив полученную формулу на ds,
получаем дифференциальное уравнение
равновесия нити
.
Разделив полученную формулу на ds,
получаем дифференциальное уравнение
равновесия нити
 (6.1
(6.1
Или в проекциях на оси декартовой системы координат, вспоминая, что , имеем
 (6.2)
(6.2)
Уравнение (6.1) можно записать и в осях натурального триэдра, при этом

и окончательно получаем
 (6.3).
(6.3).
Рассмотрим приложения полученных двух формул: задачу о прогибе нити под действием своего веса и задачу о ленточном тормозе.
Равновесие цепи под действием своего веса (рис 66).
Цепь веса Р подвешена в двух точках на одном уровне. Расстояние между точками подвеса l. Считая прогиб цепи небольшим, определить прогиб и натяжение цепи. По определению
![]()
Т .к.
прогиб цепи небольшой, то можно считать
.к.
прогиб цепи небольшой, то можно считать
![]() ,
тогда
,
тогда
![]() и уравнения (6.2) запишутся в виде:
и уравнения (6.2) запишутся в виде:
 т.е.
т.е.
![]() ,
а второе уравнение примет вид
,
а второе уравнение примет вид
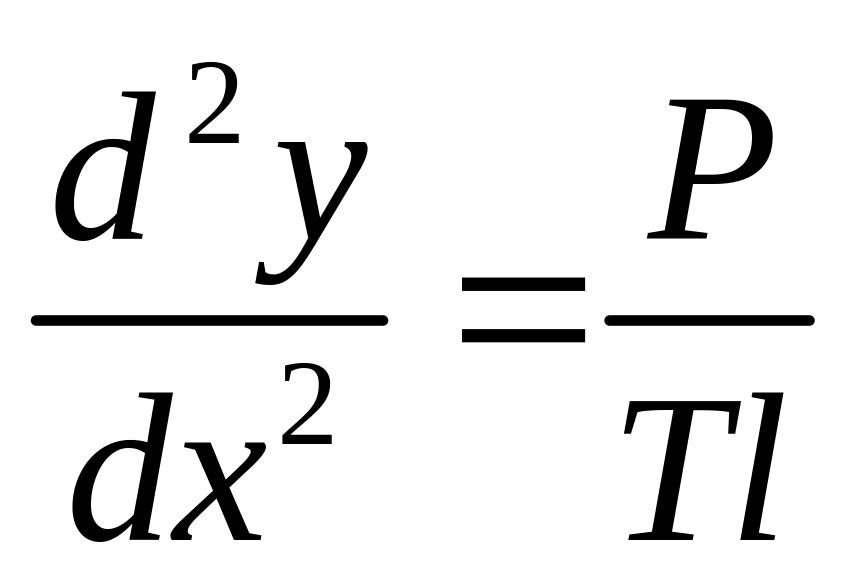 (здесь
(здесь
 ).
Интегрируя полученное выражение, получим
уравнение параболы
).
Интегрируя полученное выражение, получим
уравнение параболы
 .
.
Для
определения констант интегрирования
зададим два граничных условия
![]() .
Из первого условия
.
Из первого условия
![]() ,
а из второго
,
а из второго
 .
Окончательно получаем
.
Окончательно получаем

Максимальный
прогиб будет при
![]() и
равен
и
равен
 ,
отсюда можно получить значение натяжения
цепи в зависимости от её прогиба,
,
отсюда можно получить значение натяжения
цепи в зависимости от её прогиба,
 .
В случае, если концы цепи находятся на
разных уровнях, то в решение дифференциального
уравнения надо подставить условия
.
В случае, если концы цепи находятся на
разных уровнях, то в решение дифференциального
уравнения надо подставить условия
![]() ,
где
,
где
![]() и
и
![]() - координаты концов цепи.
- координаты концов цепи.
2. Задача о ленточном тормозе.
Н а
барабан радиуса R
(на рис 67 показана часть барабана)
находится нить АВ.
К концам которой приложены две силы
и
,
причём пусть
а
барабан радиуса R
(на рис 67 показана часть барабана)
находится нить АВ.
К концам которой приложены две силы
и
,
причём пусть
![]() .
Коэффициент трения скольжения между
нитью и барабаном f.
Надо определить: при каком соотношении
и
нить будет находиться в равновесии,
т.е. не будет скользить по барабану. В
нашем случае
.
Коэффициент трения скольжения между
нитью и барабаном f.
Надо определить: при каком соотношении
и
нить будет находиться в равновесии,
т.е. не будет скользить по барабану. В
нашем случае
![]() ,
а сила трения, направленная как показано
на рис. , равна
,
а сила трения, направленная как показано
на рис. , равна
![]() .
Тогда из уравнений (6.3) имеем
.
Тогда из уравнений (6.3) имеем
 и
и
 (*);
это дифференциальное уравнение с
разделяющимися переменными, интегрируя
которое
(*);
это дифференциальное уравнение с
разделяющимися переменными, интегрируя
которое
 ,получим
,получим
![]() .
Если
.
Если
![]() ,
то в уравнении (*) надо поменять знак
,
то в уравнении (*) надо поменять знак
![]() на
на
![]() и порядок интегрирования по φ,
тогда получим
и порядок интегрирования по φ,
тогда получим
![]() .
Окончательно условие равновесия нити
можно записать в виде
.
Окончательно условие равновесия нити
можно записать в виде
![]()
