§ 4. Примеры вычисления потенциальной энергии и работы

сил.

1. Потенциальная энергия силы тяжести вблизи поверхно­сти Земли. В большинстве технических задач можно считать поверхность Земли плоской, а силы тяжести, являющиеся ре­зультатом притяжения тел Землей, направленными по вер­тикали вниз и не изменяющимися в различных точках около­земного пространства. Рассмотрим отдельную тяжелую точку; для нее (ось z направлена по вертикали вверх) и элементарная работа определится выражением: , где Р - сила тяжести (вес) рассматриваемой точки. С другой стороны, по уравнению (121), имеем . Таким образом, dП = Pdz = d(Pz) и потенциальная энергия силы тяжести представляется формулой П = Pz + С. Для системы N тяжелых точек элементарная работа най­дется суммированием отдельных элементарных работ сил тяжести точек системы

.

И в этом случае П = . Здесь Р - общий вес системы, a - координата ее цен­тра тяжести.

2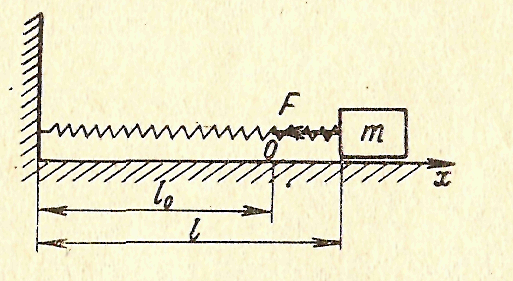 . Потенциальная энергия упругой деформации. Здесь будет исследован случай линейной теории упругости, когда материал подчиняется закону Гука. Рассмотрим упругую пружину дли­ны , один конец которой закреп­лен неподвижно (рис 62), а к другому под­вижному концу прикреплена точка массы ; при растяжении (или сжатии) пружины ее длина будет равна , а на массу действует сила, пропорциональная удлинению Рис 62

пружины . Помещая начало координат на конце недеформированной пружины, направим ось х по движению массы ; обозначая через с коэффициент жест­кости пружины, имеем

Fx =- сx, Fy = Fz = 0,

но , откуда, интегрируя, получаем

(3.93)

П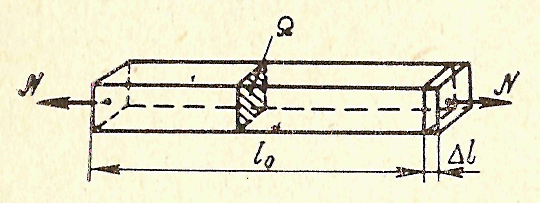 роизвольная постоянная в выражении (3.93) отброшена, так как потенциальная энергия деформации недеформированной пружины, естественно, принимается равной нулю. В эту же схему укладывается решение задачи о продоль­ной деформации (растяжении или сжатии) призматического стержня. Появляющиеся при нагружении стержня Рис 63

продольными сила­ми N нормальные напряжения пропорциональны относи­тельному удлинению ; здесь Ω - площадь попереч ного сечения, - первоначальная длина стержня. Коэффициентом пропорциональности служит мо­дуль нормальной упругости (модуль Юнга) Е, поэтому , и, таким образом, упругая сила, с которой деформирован­ный стержень действует на прикрепленную к его концу массу, будет определяться формулой

Координатой х здесь является удлинение стержня , и коэффициент жесткости с, входящий в выражение (17) для потенциальной энергии деформации, в этом случае будет равен

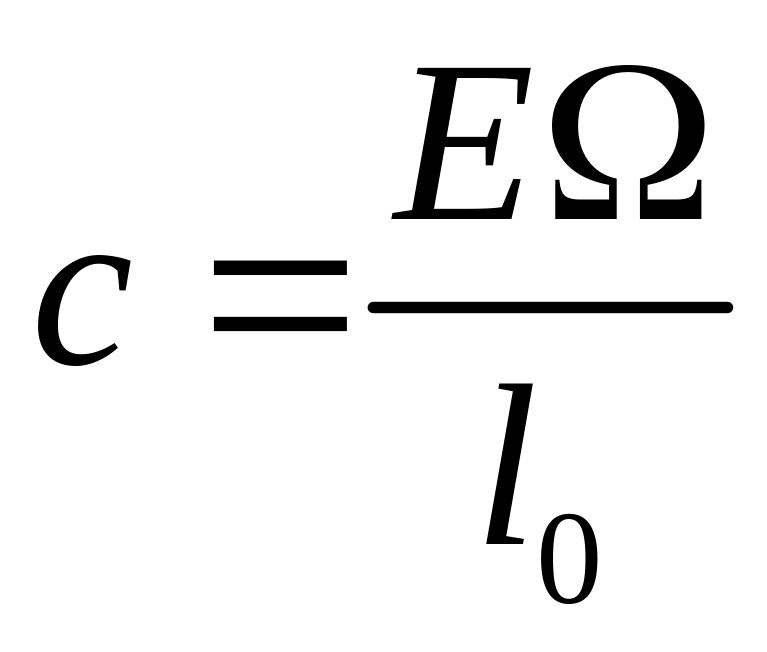
П ри изгибе балки за координату х принимается прогиб f в некоторой точке, а жесткость с зависит от размеров про­лета, расположения внешней нагрузки Рис 64.

и условий закрепле­ния балки. Так, для балки на двух шарнирных опорах, на­груженной посредине пролета сосредоточенной силой Р, жесткость следует вычислять по формуле , где - длина пролета, а - момент инерции по­перечного сечения балки. Для консольной балки будем иметь . Формула (3.93) теперь дает потенциальную энергию де­формации изгиба балки.

При кручении круглого цилиндра имеет место аналогич­ный результат. Пусть к торцам сплошного цилиндра из упругого материала приложены крутящие моменты М; размеры цилиндра: длина и радиус R считаются известными, ось z направлена по оси цилиндра. Угол закручивания на единицу длины цилиндра определяется формулой , где Mz есть упругий момент, создаваемый касательны­ми напряжениями в поперечном сечении цилиндра; G — модуль сдвига; -полярный момент инерции сечения. Та­ким образом, момент внутренних сил, действующих в сечении цилиндра, пропорционален углу поворота сечения ; элементарная работа этого момента на угле поворота будет полным дифференциалом:

Интегрируя последнее соотношение, получаем потенци­альную энергию кручения круглого стержня в виде 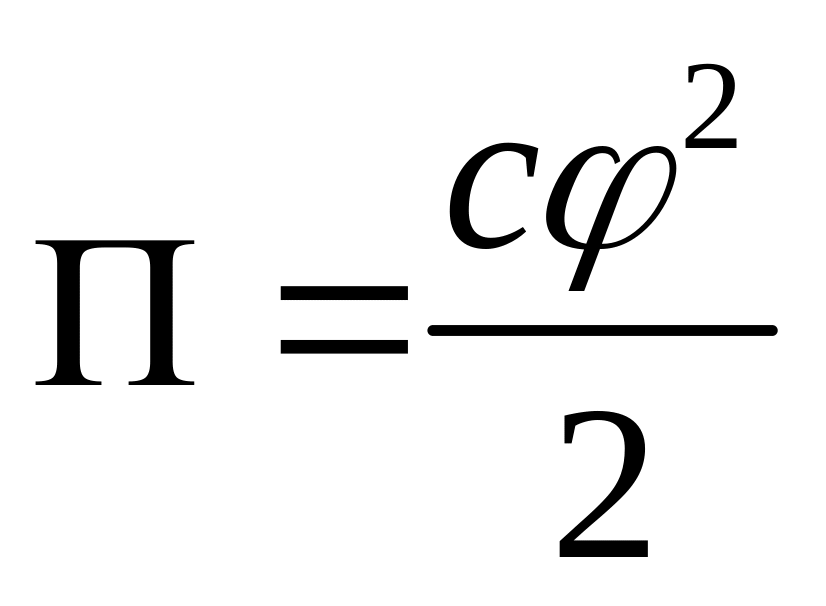, аналогичном (3.93), причем жесткость стержня на кручение, как это следует из проделанных вычислений, равна .

В приведенных примерах поведение упругой системы опи­сывалось одной координатой; возможны и более сложные (случаи, например, при одновременном растяжении, изгибе и кручении консольного стержня потенциальная энергия выражается соотношением

.

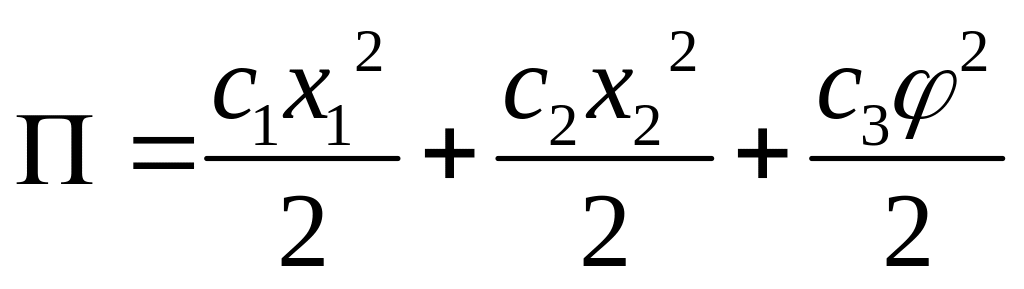3. Работа сил, приложенных к твёрдому телу.

Пусть силы ……., приложены к твердому телу в точках ……., . Выбирая произвольную точку тела О за полюс и обо­значая вектор-радиус -й точки тела , получим: , т. е. перемещение точки равно геометрической сумме пере­мещения полюса и перемещения поворота вокруг полюса ( - бесконечно малый вектор поворота). Тогда элементарная работа силы запишется в форме:

.

Второе слагаемое, согласно свойству скалярно-векторного про­изведения, может быть переписано в виде

.

Элементарная работа всех сил будет

Обозначая через - главный вектор системы сил, через - ее главный момент относительно полюса О, получим

(3.92а)

В частном случае поступательного движения твердого тела , где - элементарное перемещение, одинаковое для всех точек тела. При вращении тела вокруг неподвижной оси (пусть это будет ось Oz), выбирая за полюс точку, лежащую на оси вращения, получим .

В случае плоского движения твердого тела имеем

где через обозначен главный момент системы сил относительно оси Oz, перпендикулярной к плоскости движения и проходящей через полюс О.

4 . Работа внутренних сил, приложенных к твердому телу, выражается через главный вектор и главный момент этих сил. Работа внутренних сил взаимодействия частиц твердого тела равна нулю, так как главный вектор и главный момент этих сил равны нулю.

Рассмотрим задачу о качении цилиндра по шероховатой поверхности. Составим выра-

Рис 65. жение для элементарной работы

В этой формуле - перемещение центра диска, - поворот колеса (здесь по часовой стрелке). Перепишем полученное выражение

.

Если диск катится без скольжения, т.е. мгновенный центр скоростей находится в нижней точке диска, то и работа силы трения скольжения равна нулю и . Если диск катится с проскальзыванием, то , так как в этом случае , где f - коэффициент трения скольжения диска о поверхность.