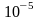3. Коефіцієнт прозорості
Однією з характеристик тунельного ефекту є коефіцієнт прозорості. За означенням коефіцієнт пропускання дорівнює відношенню інтенсивності хвилі, що проходить через бар’єр, до інтенсивності хвилі, яка падає на межу поділу двох областей. Оскільки інтенсивність хвилі пропорційна квадрату амплітуди коливань, то коефіцієнт прозорості бар’єра можна записати у вигляді:
![]()
Враховуючи співвідношення :
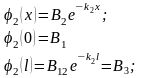
Вираз (11) можна записати у вигляді :
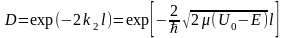 (12)
(12)
Формулу
(12) можна узагальнити на випадок
потенціального бар’єра довільної
форми. Тоді бар’єр поділяють на ряд
вузьких майже прямокутних бар’єрів
шириною
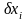 ,
для кожного з яких коефіцієнт прозорості
,
для кожного з яких коефіцієнт прозорості
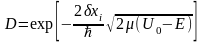
Оскільки коефіцієнт прозорості всього бар’єра дорівнює добутку коефіцієнтів прозорості окремих його ділянок, то коефіцієнт приймає вигляд:
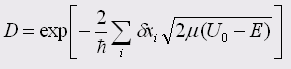
Якро товщини виділених бар’єрів вважати нескінченно малими, то співвідношення (13) має вигляд:
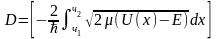 (14)З
виразу (12) виплива, що коефіцієнт
прозорості потенціального бар’єра
значною мірою залежить від його ширини
l.
Наводимо цю залежнысть для електрона,
коли
(14)З
виразу (12) виплива, що коефіцієнт
прозорості потенціального бар’єра
значною мірою залежить від його ширини
l.
Наводимо цю залежнысть для електрона,
коли
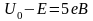 :
:
l* |
1 |
1,3 |
1,5 |
1,8 |
2 |
5 |
D |
0,101 |
0,051 |
0,032 |
0,016 |
0,008 |
1,02* |
Характерним є те, що енергія частинки, яка проходить крізь потенціальний бар’єр, не змінюється. Частинка виходить за межі бар’єру з тією ж енергією, з якою в нього входила
4. Парадоксальність "тунельного ефекту"
Проходження
частинок
через потенціальні
бар'єри
є на
перший погляд парадоксальним. Ця
парадоксальність проявляється
в
тому, що частинка,
що знаходиться усередині потенціального
бар'єру при повній енергії
,
меншої
висоти бар'єра U,
повинна
мати негативну кінетичну енергію
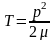 ,
і
повна енергія, як це має місце в класичній
механіці,
є сумою енергій кінетичної
і потенціальної:
,
і
повна енергія, як це має місце в класичній
механіці,
є сумою енергій кінетичної
і потенціальної:
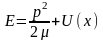
У
області, де
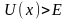 ,
,
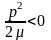 це
безглуздо, оскільки імпульс
це
безглуздо, оскільки імпульс
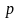 є
дійсна величина. Якраз ці області, як
ми знаємо з класичної механіки недоступні
для частинки.
Тим часом, згідно квантовій механіці,
частинка
може бути виявлена і в цій
"забороненій"
області. Таким чином
квантова
механіка приводить
до висновку,
що кінетична
енергія частинки
може бути негативною, а імпульс частинки
уявним. Цей висновок
і називають парадоксом "тунельного
ефекту".
є
дійсна величина. Якраз ці області, як
ми знаємо з класичної механіки недоступні
для частинки.
Тим часом, згідно квантовій механіці,
частинка
може бути виявлена і в цій
"забороненій"
області. Таким чином
квантова
механіка приводить
до висновку,
що кінетична
енергія частинки
може бути негативною, а імпульс частинки
уявним. Цей висновок
і називають парадоксом "тунельного
ефекту".
Насправді
тут немає жодного парадоксу, а сам
висновок
невірний. Річ у тому, що оскільки тунельний
ефект є явище квантове (при
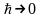 коефіцієнт прозорості
коефіцієнт прозорості
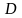 прямує
до нуля), він може обговорюватися лише
в рамках квантової механіки. Повну ж
енергію частинки
можна розглядати як суму кінетичної
і потенціальної
енергій
тільки
на основі класичної механіки. Формула
прямує
до нуля), він може обговорюватися лише
в рамках квантової механіки. Повну ж
енергію частинки
можна розглядати як суму кінетичної
і потенціальної
енергій
тільки
на основі класичної механіки. Формула
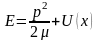 передбачає,
що одночасно знаємо величину як кінетичної
енергії
передбачає,
що одночасно знаємо величину як кінетичної
енергії
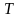 ,
так і потенціальної
.
Іншими
словами, ми приписуємо одночасно певне
значення координаті частинки
і
її імпульсу
,
що противоріче
квантовій
механіці.
Ділення повної енергії на потенціальну
і кінетичну в квантовій механіці
позбавлено сенсу, а в той же час
неспроможний і парадокс, заснований на
можливості представити повну енергію
як
суму кінетичної енергії (функція
імпульсу) і потенційної енергії (функція
координат).
,
так і потенціальної
.
Іншими
словами, ми приписуємо одночасно певне
значення координаті частинки
і
її імпульсу
,
що противоріче
квантовій
механіці.
Ділення повної енергії на потенціальну
і кінетичну в квантовій механіці
позбавлено сенсу, а в той же час
неспроможний і парадокс, заснований на
можливості представити повну енергію
як
суму кінетичної енергії (функція
імпульсу) і потенційної енергії (функція
координат).
Залишається лише поглянути, чи не може все ж виявитися так, що шляхом виміру положення частинки ми виявимо її всередині потенціального бар'єру, тоді як її повна енергія менше висоти бар'єра.
Виявити
частинку усередині бар'єру дійсно можна,
навіть якщо
;
проте
якщо фіксується координата частинки
,
при
цьому створюється, згідно співвідношення
невизначеності, додаткова дисперсія в
імпульсі
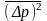 отже вже не можна стверджувати, що
енергія частинки, після того, як визначили
її положення, рівна
.
отже вже не можна стверджувати, що
енергія частинки, після того, як визначили
її положення, рівна
.
З
формули для коефіцієнта прозорості
витікає, що частинки
проникають помітним чином лише на
глибину що
визначається
рівністю
![]() .
Аби виявити частинку
усередині бар'єру, ми повинні фіксувати
її координату з точністю
.
Аби виявити частинку
усередині бар'єру, ми повинні фіксувати
її координату з точністю
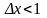 .
Але тоді неминуче виникає дисперсія
імпульсу
.
Але тоді неминуче виникає дисперсія
імпульсу
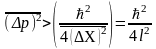
Підставляючи
сюди l2
з
,
знаходимо
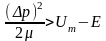 ,
тобто зміна кінетичної енергії частинки
має бути більша тієї енергії, якій їй
бракує до висоти бар'єра
.
Наведемо
ще приклад, що ілюструє це твердження.
Визначити координату частинки,
що знаходиться усередині потенціального
бар'єру таким чином,
що посилатимемо - вузький пучок світла
в напрямі, перпендикулярному до напряму
руху частинки.
Якщо пучок розсіється, то це
означає,
що на
його шляху трапилася частинка.
,
тобто зміна кінетичної енергії частинки
має бути більша тієї енергії, якій їй
бракує до висоти бар'єра
.
Наведемо
ще приклад, що ілюструє це твердження.
Визначити координату частинки,
що знаходиться усередині потенціального
бар'єру таким чином,
що посилатимемо - вузький пучок світла
в напрямі, перпендикулярному до напряму
руху частинки.
Якщо пучок розсіється, то це
означає,
що на
його шляху трапилася частинка.
Як пояснювалося вище, точність нашого виміру має бути така ; з іншого боку, не можна створити пучок світла, ширина якого була б менше довжини світлової хвилі λ, а отже, довжина хвилі світла має бути менше l, тобто
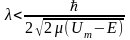 оскільки
оскільки
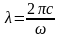 ,
де
,
де
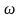 —частота
світлових коливань, а
—частота
світлових коливань, а
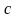 -
швидкість світла, то звідси витікає, що
-
швидкість світла, то звідси витікає, що
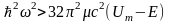
Енергії,
що зустрічаються
в нерелятивістській механіці, мають
бути менші
власної енергії частинки
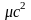 ,
тому
,
тому
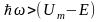 тобто
енергія вживаних в світловому пучку
квантів світла має бути більше, ніж
різниця між висотою потенціального
бар'єру і енергією частинки. Таким
чином, цей приклад ілюструє положення
про необхідність застосувати для виміру
координати прилади, що володіють досить
великою
енергією, аби можна було локалізувати
частинку.
тобто
енергія вживаних в світловому пучку
квантів світла має бути більше, ніж
різниця між висотою потенціального
бар'єру і енергією частинки. Таким
чином, цей приклад ілюструє положення
про необхідність застосувати для виміру
координати прилади, що володіють досить
великою
енергією, аби можна було локалізувати
частинку.
5. -розпад атомних ядер
Явище
радіоактивності було виявлене А.
Беккерелем в самому кінці XIX століття.
Він встановив, що атомні ядра спонтанно
(мимоволі) випускають
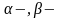 і
і
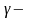 промені,
що характеризуються різною проникною
здатністю.
Незабаром після цього Э. Резерфорд і
М. Кюрі
встановили, що це
-частинки(ядра
гелію), електрони і
промені.
На початку XX століття був накопичений
значний експериментальний матеріал
про властивості радіоактивності
ядер. Зокрема, були виміряні періоди
напіврозпаду
ядер і енергії частинок,
що вилітають, і
промені,
що характеризуються різною проникною
здатністю.
Незабаром після цього Э. Резерфорд і
М. Кюрі
встановили, що це
-частинки(ядра
гелію), електрони і
промені.
На початку XX століття був накопичений
значний експериментальний матеріал
про властивості радіоактивності
ядер. Зокрема, були виміряні періоди
напіврозпаду
ядер і енергії частинок,
що вилітають, і
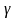 -променів.
Ці дані для
-частинок
виявилися на перший погляд несподіваними.
Так, з одного боку, енергії тих
-часток,
що вилітають для великого числа різних
ядер виявилися майже однаковими. З іншої
— періоди
напіврозпаду цих же ядер — розрізнялися
на багато порядків величини. Так,
наприклад, для
-розпаду
ядра полонія
-променів.
Ці дані для
-частинок
виявилися на перший погляд несподіваними.
Так, з одного боку, енергії тих
-часток,
що вилітають для великого числа різних
ядер виявилися майже однаковими. З іншої
— періоди
напіврозпаду цих же ядер — розрізнялися
на багато порядків величини. Так,
наприклад, для
-розпаду
ядра полонія
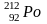 період напіврозпаду порядку
період напіврозпаду порядку
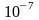 с,
а в разі ядра урану
с,
а в разі ядра урану
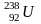 — порядка
— порядка
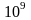 років. Цей парадокс знайшов пояснення
лише в рамках теорії тунелювання
-частинок
через потенціальний
бар’єр, що пояснив і сам факт
-розпаду
ядер.
років. Цей парадокс знайшов пояснення
лише в рамках теорії тунелювання
-частинок
через потенціальний
бар’єр, що пояснив і сам факт
-розпаду
ядер.
Тунельна теорія -розпаду була створена Г.А. Гамовим, а також Р. Герна і Е. Кондоном.
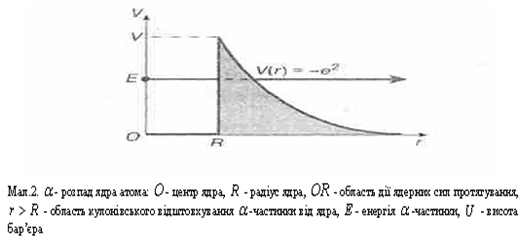
На
мал. 2 приведена схема тунелювання
-частинки
з ядра. Всередині
ядра при
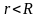 ,
де
— радіус ядра, на
-частинку
діють ядерні сили притягання,
поза ядром при
,
де
— радіус ядра, на
-частинку
діють ядерні сили притягання,
поза ядром при
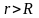 —
сили кулонівського відштовхування
від ядра. Таким чином, в області
—
сили кулонівського відштовхування
від ядра. Таким чином, в області
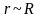 є
потенціальний
бар'єр. Висота бар'єру (в разі важких
ядер з числом нуклонів більше ста)
є
потенціальний
бар'єр. Висота бар'єру (в разі важких
ядер з числом нуклонів більше ста)
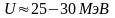 ,
а енергія
-частинки
,
а енергія
-частинки
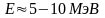 .
Чим менше
і
більше
,
тим
більша
проникність бар'єру для
-частинок
і тим менше період напіврозпаду ядра.
Експоненціальна
залежність проникності бар'єру від
різниці
.
Чим менше
і
більше
,
тим
більша
проникність бар'єру для
-частинок
і тим менше період напіврозпаду ядра.
Експоненціальна
залежність проникності бар'єру від
різниці
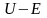 обумовлює
різкий розкид періодів напіврозпаду
для різних ядер.
обумовлює
різкий розкид періодів напіврозпаду
для різних ядер.
В 1928 Гамов, спираючись на незадовго до того часу створену квантову механіку, показав, що хвильові властивості α-частинки дозволяють їй з певною ймовірністю Р просочуватися через потенційний бар'єр. Тоді, якщо прийняти, що α-частинка існує в повністю сформованому вигляді всередині ядра, для ймовірності його α-розпаду в одиницю часу А, виникає формула:
λ = 2νP
де 2ν - число ударів α-частинки об внутрішню стінку бар'єру, яке визначається чатотою коливать ν α-частинки в середині материнського ядра. Тоді розрахувавши квантово-механічну величину Р і оцінивши ν в найпростіших наближеннях, Гамов отримав для lgТ1 / 2 закон Гейгера-Неттола, математичний вираз якого можна записати у вигляді:
![]() ,
,
де D, c - деякі сталі.
Результат Гамова мав величезний резонанс у середовищі фізиків, оскільки він продемонстрував, що атомне ядро описується законами квантової механіки

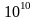 ,
м
,
м