Приложение 10

Примеры использования законов распределений СВ

в исследовании точности работы оптических приборов

(Применение одномерного и двумерного нормального распределения, распределения Рэлея, биномиального распределения для исследования влияния погрешностей оптических прицелов на результат спортивной стрельбы)

П10.1 Погрешности оптических прицелов

П10.2 Параболическое приближение траектории полета пули

П10.2.1 Дифференциальные уравнения движения материальной точки под действием приложенной силы

П10.2.2 Движение пули под действием силы тяжести после выстрела

П10.3 Моделирование явления деривации

П10.4 Влияние погрешностей ввода углов прицеливания на положение центра рассеивания точек попадания в мишень

П10.5 Влияние параллакса в оптических прицелах на точность стрельбы

П10.5.1 Угловой и линейный параллакс между шкалой и индексом

П10.5.2 Параллакс в телескопической системе и формы его представления

П10.5.3 Допустимый и остаточный параллакс в оптическом прицеле

П10.5.4 Порядок расчета

П.10.1. Погрешности оптических прицелов

В п.5.9.3 отмечено, что при стрельбе по мишени из спортивной винтовки с установленным на ней оптическим прицелом на результат стрельбы влияют баллистические характеристики оружия (например, рассеивание траекторий из-за разности пороховых зарядов в патронах, различия в формах пуль), условия стрельбы (влажность воздуха, давление, температура, наличие ветра, его направление и др.), опытность спортсмена, характеризуемая погрешностью наведения на мишень, погрешность определения дальности до нее, а также погрешности изготовления, сборки, юстировки и выверки самого прицела.

В последних случаях это обусловлено тем, что при наличии отдельной погрешности или в результате их совокупного действия неточно вводится угол прицеливания  в вертикальной плоскости (рис. 5.9.6). Поэтому увеличивается рассеивание точек попадания в мишень, а срединная траектория полета пуль смещается относительно расчетной и пересекает мишень не в ее центре. В результате уменьшается вероятность попадания в мишень.

Аналогичное действие оказывают и эксплуатационные погрешности, возникающие по мере износа и смещения деталей прицела от ударных воздействий при стрельбе и появления чрезмерных зазоров в механизмах ввода вертикальных и горизонтальных углов прицеливания.

В соответствии с методикой точностного расчета оптических прицелов их допустимые систематические и случайные погрешности определяются долей от суммы всех других случайных составляющих погрешности стрельбы, источники которых не связаны с самим прицелом и приводят к рассеиванию точек попадания в мишень.

Дополнительная случайная погрешность _пр, характеризующая рассеивание точек попадания в мишень от прицела, не должна увеличивать рассеивание от причин, не связанных с прицелом, более, чем на 10% (и, соответственно, уменьшать вероятность попадания):

, т.е. ; (П10.1)

где ₀ – СКО точек попадания в мишень; ₁ – составляющая общей случайной погрешности ₀, не зависящая от прицела; _Б – баллистическая составляющая; _н – составляющая, обусловленная наведением оружия с прицелом на мишень; _м – составляющая от определения положения мишени (например, от измерения дальности до нее).

Таким образом, случайная составляющая рассеивания _пр точек попадания в мишень от прицела не должна быть больше половины суммарной случайной составляющей ₁, не связанной с прицелом.

Дополнительная систематическая погрешность стрельбы от прицела _m,пр характеризует смещение срединной траектории с центра мишени. В этом случае плотность вероятности координат точек попадания в мишень изменяется по зависимости f(x) (рис. П10.1), а указанное смещение приводит к уменьшению вероятности попадания в небольшую (по сравнению с ₁) мишень размером l  ₁ приблизительно до величины f_ l, где:

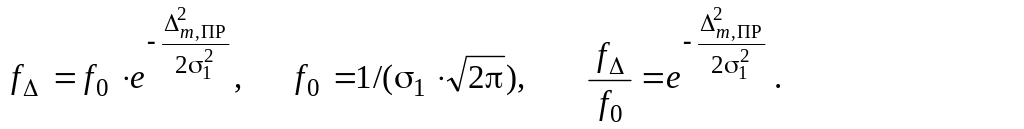(П10.2)

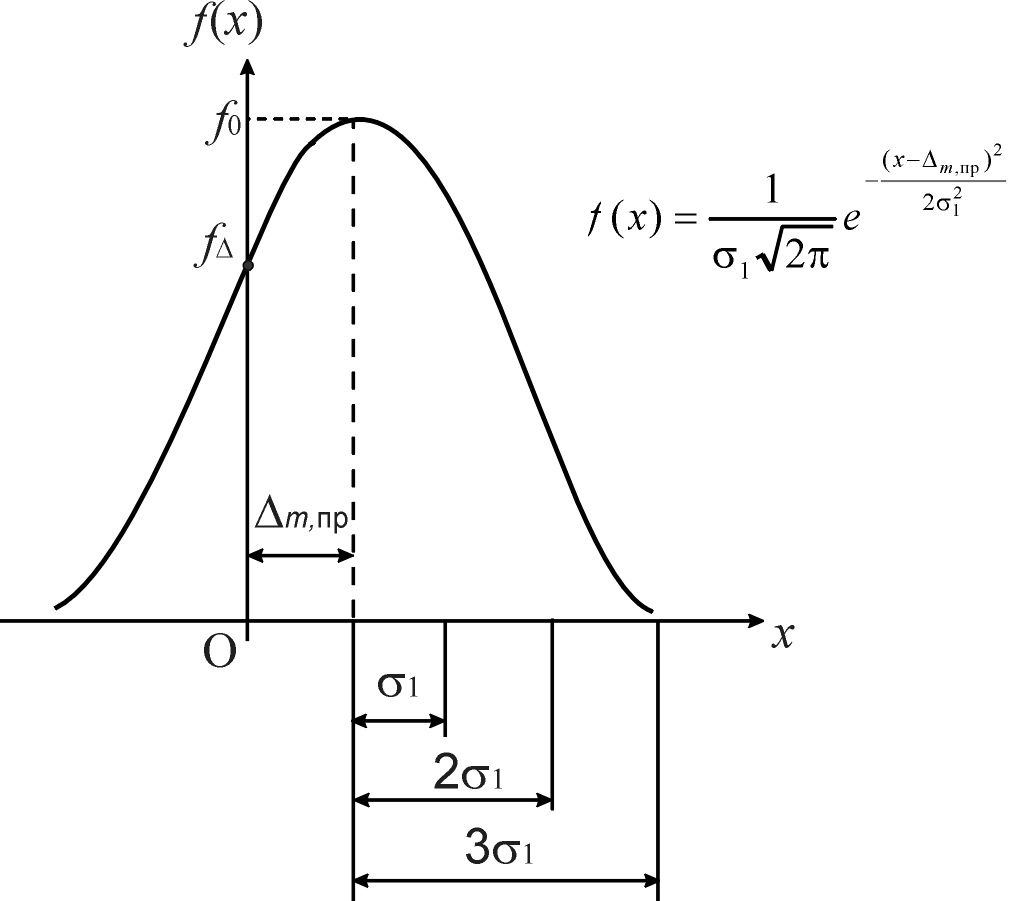
Рис. П10.1. Изменение (смещение) графика плотности вероятности

координат точек попадания в мишень f(x) при наличии

систематической погрешности прицела _m,,пр (0- центр мишени)

При проектировании прицела допускают снижение значения f_ не более, чем на 10% от f₀:

f_  0,9 f₀, f_  f₀  0,9, .

После логарифмирования получаем:

^. (П10.3)

Таким образом, составляющая систематической погрешности стрельбы от прицела _m,пр не должна превосходить 0,4 _1.

Общая систематическая погрешность стрельбы:

 _{m, 0} =  _{m, Б}+ _{m, н} + _{m, м}+ _m,пр. (П10.4)

Здесь _m,Б – баллистическая составляющая систематической погрешности (например, от разгара ствола винтовки во время стрельбы); _m,н – составляющая систематической погрешности от наведения на мишень (характеризует опытность стрелка); _m,м – составляющая от определения положения мишени (например, систематическая погрешность измерения дальности до нее).

При разработке прицелов бывает необходимо установить влияние отдельных погрешностей, из которых состоят суммарные _пр и _m,пр. Например, принимая в основу устройства прицела какие-то допущения, важно оценить, в какой мере эти допущения будут ухудшать результаты стрельбы.

При анализе систематических составляющих самой погрешности прицела _m,пр сравнивают их влияние между собой на результат стрельбы с целью выявления доминирующих. Важно заметить здесь, что _m,пр – результат расчета влияния этих составляющих на смещение графика плотности вероятности координат точек попадания в мишень (смещение центра рассеивания с центра мишени, рис. П10.1). Чтобы его получить, надо знать траекторию полета пули до мишени. При этом часто пользуются параболическим приближением для нее.

П10.2. Параболическое приближение траектории полета пули

П10.2.1. Дифференциальные уравнения движения материальной точки под действием приложенной силы

Пусть материальная точка М массой m движется в декартовой системе координат oxyz под действием силы (рис. П10.2). Здесь - радиус-вектор точки М, - векторное ускорение. Тогда закон движения можно записать в виде:

. (П10.5)

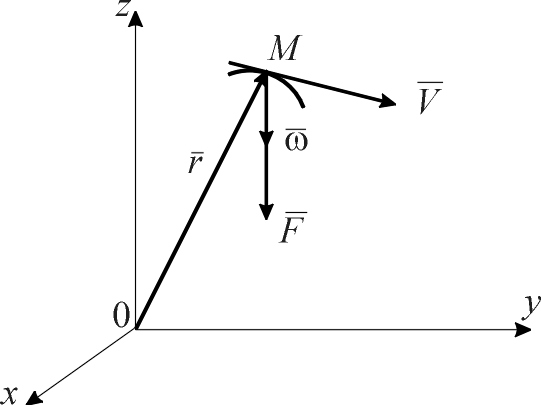
Рис. П10.2. Движение материальной точки М под действием силы

Сила зависит от положения точки М, ее скорости, времени от начала движения (т.е. от , , t или от x, y, z, x, y, z, t). Спроектируем векторное уравнение (П10.5) на оси координат:

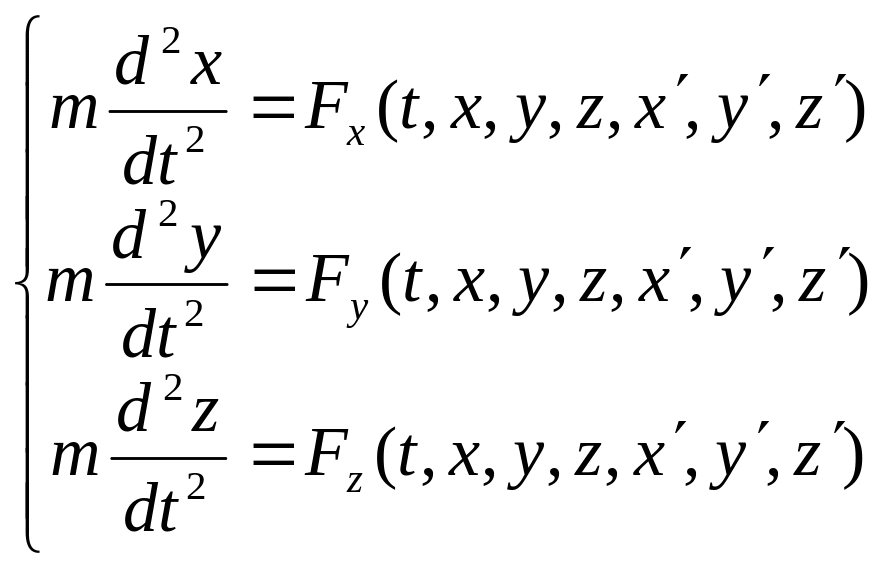(П10.6)

Здесь F_x, F _y, F _z - проекции на оси координат. Это система обыкновенных дифференциальных уравнений 2-го порядка, для которой решим задачу Коши.

Найдем решение, удовлетворяющее начальным условиям:

при t = t_0, x=x₀, y = y₀, z = z₀, x = x₀, y = y₀, z = z_0.

Здесь векторы и определяют начальное положение и скорость точки М в момент начала движения t = t₀.

Общее решение системы (П10.6) имеет вид:

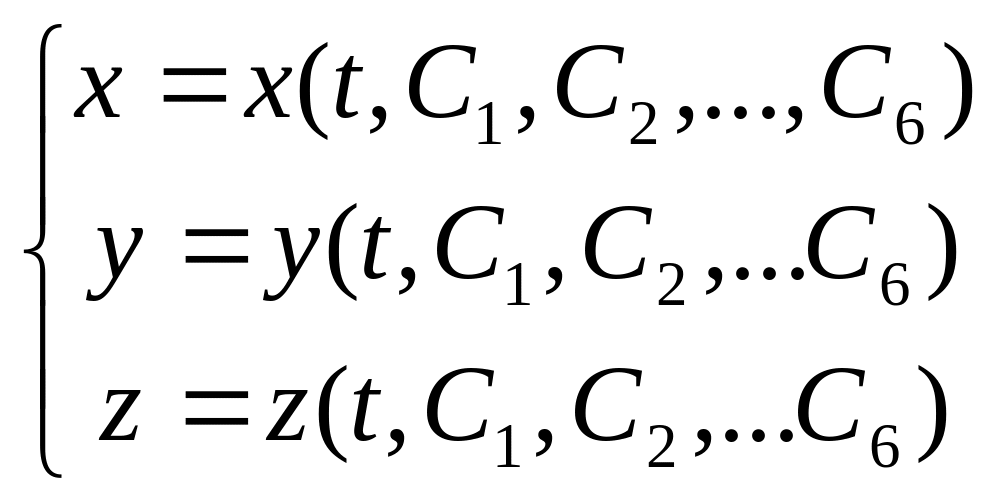(П10.7)

Здесь C_1, C_2,… _,C₆ – произвольные постоянные, однозначно определяемые начальными условиями. Подставив их в (П10.7), получаем:

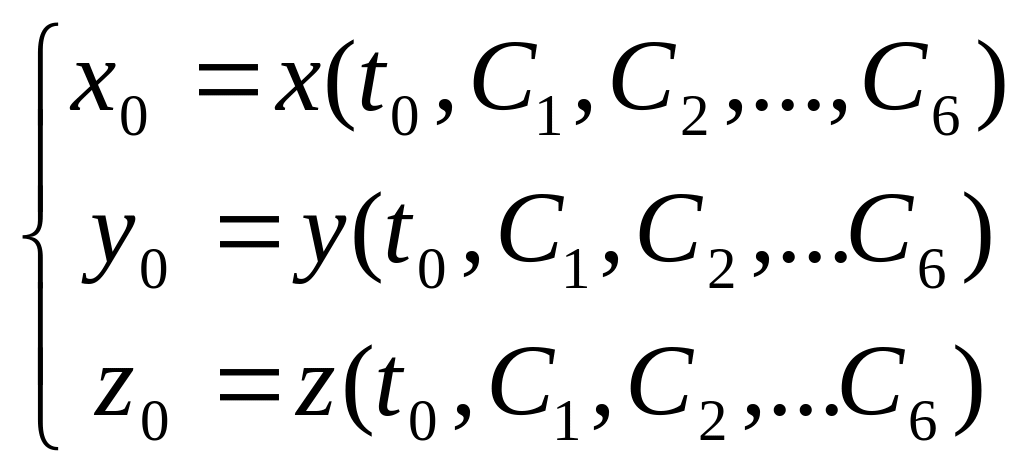
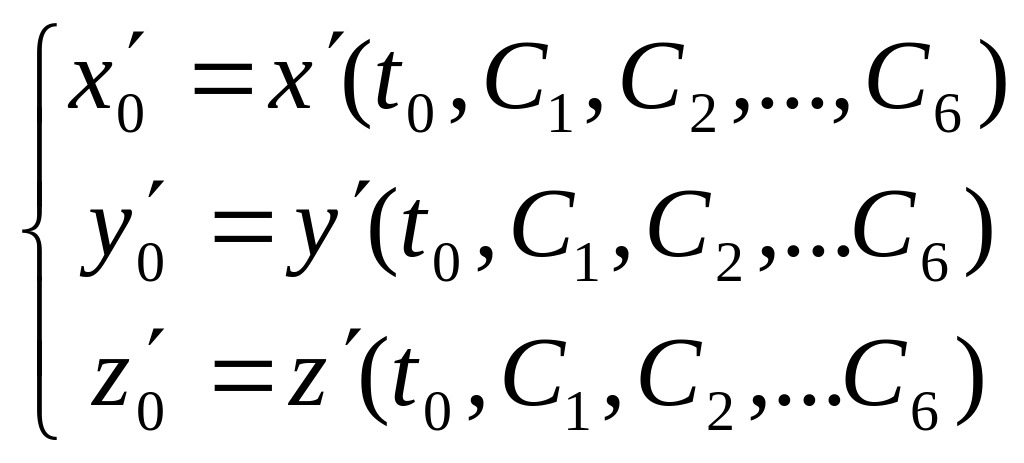(П10.8)

Из (П10.7) и (П10.8) определяются постоянные С_1, С_2,…, С₆ .

С_к = f_к(t_0, x₀, y₀, z₀, x₀, y₀, z₀), к =1,2,…,6.

Описанные дифференциальные уравнения движения материальной точки дают возможность рассмотреть две задачи.

1. По заданному движению точки найти действующую на нее силу, которая вызвала это движение (прямая задача динамики).

2. По заданной силе найти закон движения точки.

Для решения первой задачи, зная закон движения точки , по формуле (П10.5) достаточно найти производную второго порядка радиус-вектора .

Для решения второй задачи, которое дано ниже, надо проинтегрировать систему (П10.6). Для общих выражений функций F_x, F_у, F_z получение решений в виде квадратур невозможно. Однако часто для конкретных заданных сил такое решение системы удается записать и в квадратурах. Рассмотрим такой случай. (Более подробно эти вопросы рассмотрены в специальной литературе).

П10.2.2. Движение пули под действием силы тяжести после выстрела

Определим траекторию полета пули. Пусть материальная точка М (пуля) массой m движется после вылета из ствола винтовки со скоростью и на нее действует сила тяжести = (0,0, - mg) так, как показано на рис. П10.3 (g – ускорение силы тяжести).

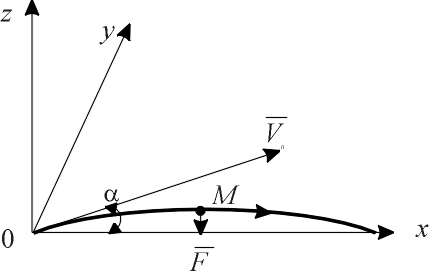
Рис. П10.3. Движение пули под действием силы тяжести после выстрела

По формулам (П10.6) составляем систему дифференциальных уравнений для этого случая (П10.9) и после интегрирования её получаем (П10.10):

(П10.9) . (П10.10)

Зададим начальные условия движения пули и найдём значения произвольных постоянных. При t₀=0 выстрел производится в точке 0 со скоростью вылета пули (рис.П10.3):

. (П10.11)

Подставив начальные условия в общее решение (П10.10), получаем

 С₄ =С₅ = С₆ =0 (П10.12)

 (П10.13)

Найденные значения С_1, С₂,…. С₆ подставляем в общее решение (П10.10) и получаем частное в виде:

(П10.14)

Таким образом, движение происходит в вертикальной плоскости 0XZ. Из первого уравнения находим t и подставляем в третье, получаем уравнение траектории:

. (П10.15)

Пуля движется в плоскости 0XZ по параболе.

Чтобы найти дальность полёта, надо определить точки её пересечения с осью ox (в этом случае z = 0). Из (П10.15) следуют два решения:

х₁ = 0 (очевидное решение; это точка выстрела х₀),

х₂ = D = V₀²sin2/g; D_max= V₀²/g . (П10.16)

Наибольшая дальность D_max получается при  = /4, (sin2 = 1).

Замечание. Поскольку sin2 = sin(-2), то, обозначив   2) - , получим x₂ = D = V₀²sin2/g. Это означает, что дальность стрельбы одинакова для углов прицеливания  и  = 2) - .

Е сли скорость V₀ известна, дальность до мишени D измерена дальномером или другими средствами, угол прицеливания  определяется по таблицам стрельбы для конкретного типа боеприпасов. Приближённо его можно найти из (П10.16):

 = 0,5arcsin(Dg/V₀²) , (П10.17)

если мишень находится на горизонте оружия.

П10.3. Моделирование явления деривации

В рассмотренной модели движения пули не учитывалось сопротивление воздуха и некоторые другие факторы, например, её вращение вокруг продольной оси. Оно происходит из-за специальной нарезки канала ствола винтовки в виде спиральных канавок. Это делается для большей стабильности траектории полёта пули в воздухе, что уменьшает рассеивание. Однако возникает опрокидывающий момент от трения в воздухе и отклонение траектории в боковом направлении от приложенной силы P = ma. Описанное явление называют деривацией. В результате требуется вводить поправку – угол прицеливания  в горизонтальной плоскости (рис. П10.4).

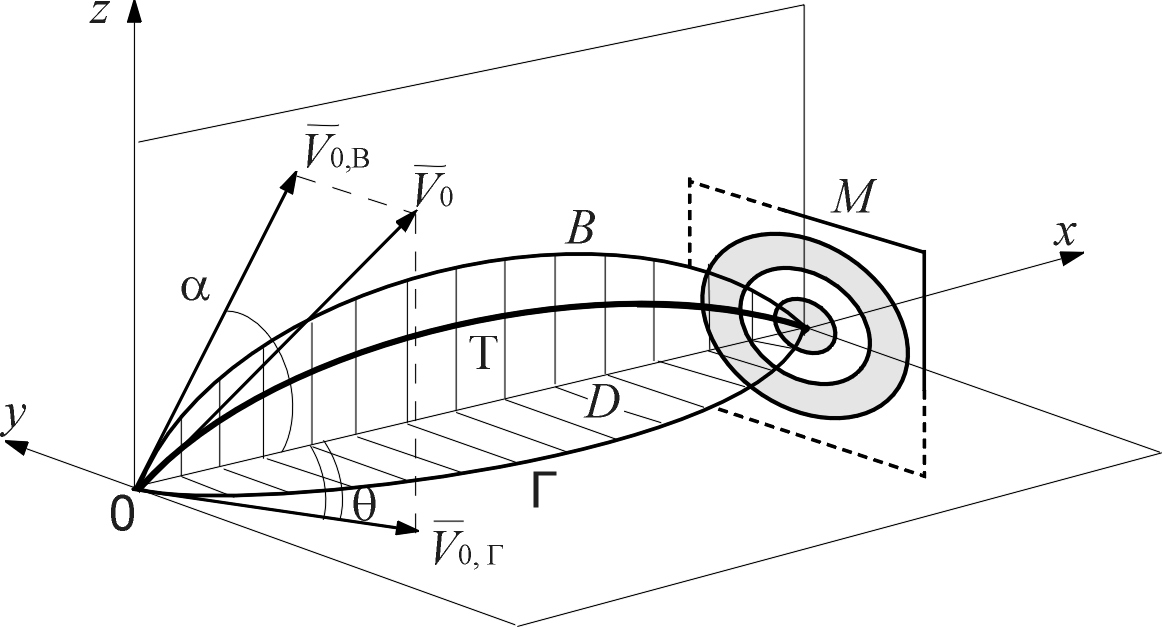
Рис. П10.4. Траектория полёта пули «Т» и её проекции на вертикальную «В» и горизонтальную «Г» плоскости; 0 – точка выстрела; М – мишень; D– дальность до мишени;  и  - углы прицеливания в вертикальной и горизонтальной плоскостях; V₀,V_0,В, V_0,Г  начальная скорость и её проекции.

Поэтому в оптическом прицеле перекрестие сетки смещается не только в вертикальном направлении для ввода угла прицеливания , но и в горизонтальном для ввода угла прицеливания . Направление последнего зависит от направления вращения пули. При его изменении на противоположное проекция «Г» траектории сместится в область положительных значений у.

Реальная траектория полёта пули «Т» сложная, поэтому для приближённых расчётов при малых углах  и  примем V₀ V_0,В  V_0,Г. Будем считать на основании п.10.2.2 проекции «В» и «Г» траектории «Т» параболами. Уравнение первой дано в (П10.15) и по аналогии с (П10.16) и (П10.17) для дальности D и угла прицеливания  в горизонтальной плоскости запишем:

D=-V₀² sin2/a,  = -0,5arcsin(Da/V₀ ²). (П10.18)

В последнем случае удаётся учесть влияние погрешности  ввода угла  в оптическом прицеле на результат стрельбы и смоделировать тем самым явление деривации. Важно, чтобы указанные допущения сохранялись одинаковыми при сравнении влияния на результат стрельбы всех источников погрешностей ввода углов  и . Знак «минус» в правой части формулы (П10.18) учитывает направление горизонтальной проекцииV_0,Г вектора начальной скорости пули V₀ в сторону отрицательных значений «у» (угол  на рис. П10.4 считается отрицательным).