
3.5. Арифметические действия со сходящимися последовательностями
Теорема 1. (
Об арифметических
действиях со сходящимися последовательно-
стями ) Пусть
,
![]() .
Тогда:
.
Тогда:
а) последовательность
![]() сходится, а ее предел равен a
b;
сходится, а ее предел равен a
b;
б) последовательность
![]() сходится, а ее предел равен ab;
сходится, а ее предел равен ab;
в) если при всех
![]() и, кроме того,
и, кроме того,
![]() ,
то последовательность
,
то последовательность
![]() сходится, а ее
предел равен
сходится, а ее
предел равен
![]() .
.
Так
как
и
,
то (
п. 3.4.,замечание 2, )
![]() и
и
![]() ,
где
и
.
,
где
и
.
а) ![]() ,
где
,
где
![]() .
Так как
.
Так как
![]() и
и
![]() ,
то и
,
то и
![]() .
Таким образом,
.
Таким образом,
![]() ,
где
,
где
![]() ,
поэтому ( п. 3.4.,замечание 2 )
,
поэтому ( п. 3.4.,замечание 2 )
![]() .
.
б) ![]() ,
где
,
где
![]() .
Так как
и
,
то
.
Так как
и
,
то
![]() ,
,
![]() ( п.3.4., следствие теоремы 2) и
( п.3.4., следствие теоремы 2) и
![]() ;
поэтому
.
Таким образом,
;
поэтому
.
Таким образом,
![]() ,
где
;
значит,
,
где
;
значит,
![]() .
.
в) ![]() .
.
Обозначим:
![]() ,
,
![]() ,
,
![]() Последовательность
Последовательность
![]() ограничена. Действительно, так как
,
то либо
ограничена. Действительно, так как
,
то либо
![]() ,
либо
,
либо
![]() .
Пусть
(случай
рассматривается аналогично). Выберем
некоторое p,
.
Пусть
(случай
рассматривается аналогично). Выберем
некоторое p,
![]() .
По теореме о стабилизации знака
неравенства ( п. 3.3., теорема 3 ) найдется
натураль- ное
.
По теореме о стабилизации знака
неравенства ( п. 3.3., теорема 3 ) найдется
натураль- ное
![]() такое, что
такое, что
![]() при всех
.
Отсюда: 0
при всех
.
Отсюда: 0
![]() при
,
т.е.,
при
,
т.е.,
![]() при всех
.
Обозначим через
при всех
.
Обозначим через
![]() и
и
![]() соответственно наименьшее и наибольшее
из чисел
соответственно наименьшее и наибольшее
из чисел
![]() ,
,
![]() ,
,
,
,
![]() и пусть
и пусть
![]() ,
,
![]() .
Очевидно, все члены последовательности
лежат на сегменте
.
Очевидно, все члены последовательности
лежат на сегменте
![]() ,
т.е. эта последовательность ограничена.
Последовательность
,
т.е. эта последовательность ограничена.
Последовательность
![]() есть б.м. последователь- ность, так как
и
.
Значит,
есть б.м. последователь- ность, так как
и
.
Значит,
![]() является произведением ограничен- ной
последовательности
и б.м. последовательности
,
поэтому ( п. 3.4., теорема 2 )
.
является произведением ограничен- ной
последовательности
и б.м. последовательности
,
поэтому ( п. 3.4., теорема 2 )
.
Итак,
![]() ,
где
.
Значит, ( п 3.4., теорема 3),
,
где
.
Значит, ( п 3.4., теорема 3),
![]() .
.
3.6. Теоремы о монотонных последовательностях
Теорема 1. ( Признак Вейерштрасса сходимости монотонной последова-
тельности )
Если неубывающая последовательность
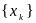 ограничена сверху, то она сходится, а
ее предел равен
ограничена сверху, то она сходится, а
ее предел равен
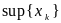
Если невозрастающая последовательность {x k} ограничена снизу, то она сходится, а ее предел равен inf {x k}
1) Обозначим:
![]() .
Покажем, что последовательность
и число a
удовлетворяют определению 1, п.3.2., а
именно, что
.
Покажем, что последовательность
и число a
удовлетворяют определению 1, п.3.2., а
именно, что
![]()
![]()
![]() .
.
Пусть задано
некоторое
![]() .
Так как a
– точная верхняя грань для
,
то
.
Так как a
– точная верхняя грань для
,
то
![]() при всех
,
а число
при всех
,
а число
![]() не является верхней гранью для
.
Зна- чит, найдется член последовательности
– обозначим его через
не является верхней гранью для
.
Зна- чит, найдется член последовательности
– обозначим его через
![]() (здесь
– номер этого члена последовательности
) – такой, что
(здесь
– номер этого члена последовательности
) – такой, что
![]() .
Рассматриваемая после- довательность
- неубывающая, значит,
.
Рассматриваемая после- довательность
- неубывающая, значит,
![]() при всех
и потому при всех
выполняется
при всех
и потому при всех
выполняется
![]() .
Но если
.
Но если
![]() ,
то, очевидно,
,
то, очевидно,
![]() ;
следовательно, мы установили, что
;
следовательно, мы установили, что
![]() .
Число
здесь – произвольное положительное
число, так что
.
Число
здесь – произвольное положительное
число, так что
;
значит,
![]()
2) Доказательство этого утверждения проводится аналогично.
Упражнение . Провести доказательство утверждения 2).
Теорема 2. (
О
вложенных
сегментах ) Пусть
задана бесконечная последо- вательность
сегментов
![]() ,
,
![]() ,
,
,
,
![]() ,
, где
,
, где
![]() при всех
,
и пусть
при всех
,
и пусть
![]() .
Если 1) при всяком
сегмент
содержит после- дующий сегмент
.
Если 1) при всяком
сегмент
содержит после- дующий сегмент
![]() и 2)
и 2)
![]() ,
то существует единственное число ,
принадлежащее всем сегментам этой
последовательности: ..
,
то существует единственное число ,
принадлежащее всем сегментам этой
последовательности: ..
Из условия 1)
следует, что последовательность
![]() левых концов сег -ментов является
неубывающей, а последовательность
левых концов сег -ментов является
неубывающей, а последовательность
![]() правых концов – невоз- растающей.
Последовательность
правых концов – невоз- растающей.
Последовательность
![]() ограничена сверху (например, числом
ограничена сверху (например, числом
![]() ),
зна- чит, она сходится: обозначим ее
предел через
),
зна- чит, она сходится: обозначим ее
предел через
![]() .
Последовательность
.
Последовательность
![]() ограни- чена снизу (например, числом
ограни- чена снизу (например, числом
![]() ),
значит, она сходится; обозначим ее предел
через
),
значит, она сходится; обозначим ее предел
через
![]() .
Из утверждений 1) и 2) теоремы 1 имеем :
.
Из утверждений 1) и 2) теоремы 1 имеем :
![]() ,
,
![]() ;
поэтому при всех
;
поэтому при всех
![]()
![]() и
и
![]() .
Кроме того, в силу теоремы о предельном
перехо- де в неравенстве (п.3.3.) из
следует
.
Кроме того, в силу теоремы о предельном
перехо- де в неравенстве (п.3.3.) из
следует
![]() .
Следовательно, при всех
.
Следовательно, при всех
![]()
![]() .
Покажем, что
.
Покажем, что
![]() .
.
Допустим противное:
![]() .
Обозначим :
.
Обозначим :
![]() .
Тогда из
.
Тогда из
![]()
![]() следует:
следует:
![]() при всех
,
что противоречит условию
теоремы. Значит,
.
при всех
,
что противоречит условию
теоремы. Значит,
.
Итак, мы доказали,
что последовательности
и
имеют один и тот же предел
![]() ,
который, очевидно, принадлежит каждому
из сегментов
,
.
Докажем теперь, что
– единственная точка, принадлежащая
всем сегментам
,
.
,
который, очевидно, принадлежит каждому
из сегментов
,
.
Докажем теперь, что
– единственная точка, принадлежащая
всем сегментам
,
.
Предположим
противное: пусть существует вещественное
число
, отличное от
и принадлежащее каждому сегменту
![]() :
:
![]()
![]() .
Обозначим :
.
Обозначим :
![]() .
Так как
и
принадлежат сегменту
,
то
.
Так как
и
принадлежат сегменту
,
то
![]()
![]() =
=![]() .
Значит, при всех
,
а это противоречит тому, что
.
Следовательно,
– единственная точка, общая всем
сегментам
,
.
.
Значит, при всех
,
а это противоречит тому, что
.
Следовательно,
– единственная точка, общая всем
сегментам
,
.
Теорема 3.
Последовательность
![]() сходятся
.
сходятся
.
Рассмотрим
последовательность
,
где x
k
=
![]() Докажем, что это убывающая последовательность;
для этого, очевидно, достаточно установить,
что при всех
отношение
Докажем, что это убывающая последовательность;
для этого, очевидно, достаточно установить,
что при всех
отношение
![]() меньше единицы. Имеем:
меньше единицы. Имеем:
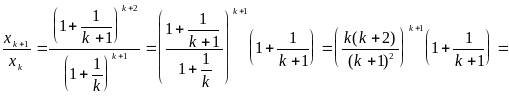
![]() .
.
Воспользовавшись неравенством Бернулли ( п. 2.5.) получим :
![]() ;
;
отсюда :
![]() .
.
Заметим:
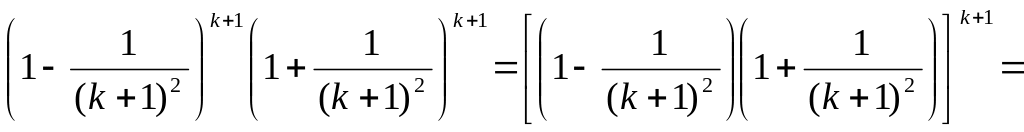 .
.
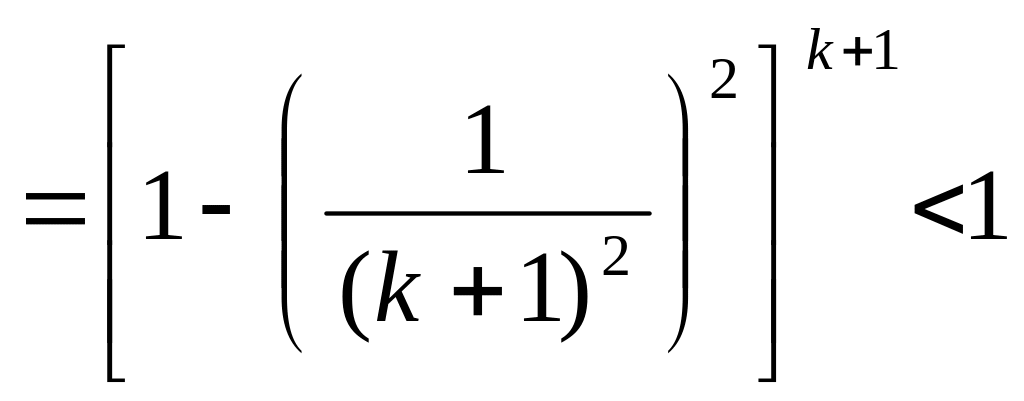 .
Отсюда:
.
Отсюда:
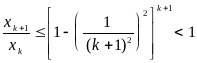 при всех
.
Итак, последовательность
при всех
.
Итак, последовательность
![]() является убывающей последовательностью.
Так как
является убывающей последовательностью.
Так как
![]() ,
то и
,
то и
![]() при всех
,
т.е.
ограничена снизу числом 1. По теореме
1 она сходится. ◄
при всех
,
т.е.
ограничена снизу числом 1. По теореме
1 она сходится. ◄
Предел
последовательности
обозначим через е:
![]() .
.
Следствие.
![]() .
.
► Для последовательности
,
где
![]() можем записать:
можем записать:
![]() .
Предел знаменателя этой дроби равен
1, предел ее числителя равен e;
по теореме 1,п.3.5., получим :
.
Предел знаменателя этой дроби равен
1, предел ее числителя равен e;
по теореме 1,п.3.5., получим : ![]() .
◄
.
◄
Замечание. Было
установлено (см. доказательство теоремы),
что последова- тельность
![]() убывает, значит,
убывает, значит,
![]() .
Mожно показать, что последовательность
.
Mожно показать, что последовательность
![]() возрастает; отсюда:
возрастает; отсюда:
![]() ,
Таким образом,
,
Таким образом,
![]() N
N
![]()
![]() ,
причем
,
причем
![]() .
Это дает возможность вычислять любое
количество первых десятичных знаков
числа e:
.
Это дает возможность вычислять любое
количество первых десятичных знаков
числа e:
e =2,718281828459045 .
Константа e – одна из важнейших в математике. В частности, она является основанием наиболее употребительной системы логарифмов. Логарифм числа x, x > 0, по основанию e называют натуральным логарифмом числа x и обозначают через lnx. Отметим связь между десятичным и натуральным логарифмами числа x :
![]() ,
где M
= lge
=
,
где M
= lge
=
![]() =
0,434294… .
=
0,434294… .
3.7. Бесконечно большие последовательности
Среди расходящихся последовательностей наибольший интерес представляют бесконечно большие последовательности. В определенном смысле это понятие проти- воположно понятию бесконечно малой последовательности.
Определение 1.
Будем говорить, что последовательность
![]() стремится к ,
если для всякого положительного числа
E
существует натуральное
стремится к ,
если для всякого положительного числа
E
существует натуральное
![]() такое, что для всех ее членов х
,
номер k
которых превышает
,
справедливо неравенство
такое, что для всех ее членов х
,
номер k
которых превышает
,
справедливо неравенство
![]() ,
т.е. если
,
т.е. если
![]()
![]()
![]() .
.
Геометрически
требования этого определения означают,
что все члены остатка
![]() лежат на числовой оси правее точки E.
Таким образом, правее точки E
ле- жит бесконечное множество членов
последовательности
,
в то время, как левее этой точки может
находиться разве лишь конечное их
количество. Существенно, что сказанное
остается справедливым при любом E
0, которое может быть взято как угодно
большим. Если условия этого определения
выполнены, будем записывать:
лежат на числовой оси правее точки E.
Таким образом, правее точки E
ле- жит бесконечное множество членов
последовательности
,
в то время, как левее этой точки может
находиться разве лишь конечное их
количество. Существенно, что сказанное
остается справедливым при любом E
0, которое может быть взято как угодно
большим. Если условия этого определения
выполнены, будем записывать:
![]() или
или
![]() .
Очевидно, такая последовательность не
ограничена сверху.
.
Очевидно, такая последовательность не
ограничена сверху.
Определение 2.
Будем говорить, что последовательность
стремит- ся к –,
если для всякого положительного числа
E
существует натуральное
та- кое, что для всех тех ее членов х
,
номер k
которых превышает
,
справедливо неравенство
![]() ,
т.е., если
,
т.е., если
![]()
![]() .
.
Если условия этого
определения выполнены, будем записывать:
![]() или
или
![]() .
Очевидно, такая последовательность не
ограничена снизу.
.
Очевидно, такая последовательность не
ограничена снизу.
Упражнение.
1) Доказать,
что если неубывающая последовательность
не ограничена сверху, то
![]() .
2) Доказать, что если невозрастающая
последова- тельность
не ограничена снизу, то
.
.
2) Доказать, что если невозрастающая
последова- тельность
не ограничена снизу, то
.
Определение 3.
Будем говорить, что последовательность
стремится к ,
если для всякого положительного числа
E
существует натуральное
![]() такое,
что для всех ее членов х
,
номер k
которых превышает
,
справедливо неравенство
такое,
что для всех ее членов х
,
номер k
которых превышает
,
справедливо неравенство
![]() ,
т.е., если
,
т.е., если
![]() .
.
Если условия этого
определения выполнены, будем записывать
![]() или
или
![]() .
.
Последовательности,
стремящиеся к ,
к –
или к ,
называют бесконечно
большими
последовательностями (б.б.
последовательностями). Б.б. последователь-
ность является расходящейся
последовательностью. В самом деле, пусть
–
б.б. последовательность, и пусть a
– некоторое вещественное число, а
– некоторое положительное число. Из
определений 1, 2 и 3 вытекает, что на
ограниченном интервале
![]() может находиться разве лишь конечное
множество членов последовательности
,
поэтому a
не является ее пределом. Но a
– произвольное вещественное число.
Значит, ни одно вещественное число не
может быть пределом б.б. последовательности
,
т.е. она расходится.
может находиться разве лишь конечное
множество членов последовательности
,
поэтому a
не является ее пределом. Но a
– произвольное вещественное число.
Значит, ни одно вещественное число не
может быть пределом б.б. последовательности
,
т.е. она расходится.
Отметим еще, что если последовательность удовлетворяет определению 1 или определению 2, то она удовлетворяет и определению 3. Если же , то это не означает, что обязательно стремится либо к , либо к –.
Пример 1. Пусть
![]() ,
где
,
где
![]() .
Если q
1, то
.
Если q
1, то
![]() ,очевидно, воз- растает и не ограничена
сверху; поэтому ( см. выше, Упражнение )
,
можно также написать
.
Если же q
–1, то
,
причем
не стремится ни к ,
ни к –.
,очевидно, воз- растает и не ограничена
сверху; поэтому ( см. выше, Упражнение )
,
можно также написать
.
Если же q
–1, то
,
причем
не стремится ни к ,
ни к –.
Теорема 1. ( О связи между б.б. и б.м. последовательностями ).
Пусть задана
последовательность
,
причем
![]() при всех
.
Обозначим
при всех
.
Обозначим
![]() Тогда 1) если
Тогда 1) если
![]() ,
то
,
то
![]() ;
2) если
,
то
.
;
2) если
,
то
.
Докажем утверждение
1). Пусть E
0 – некоторое число; обозначим :
![]() .
Так как
,
существует
такое, что
.
Так как
,
существует
такое, что
![]() ; отсюда :
; отсюда :
![]() .
.
Таким образом,
если положить
![]() ,
то имеем
,
то имеем
![]()
![]() .
Так как здесь E
0 – произвольное положительное число,
то условия определения 3 выполня -ются
для последовательности
;
значит,
.
Так как здесь E
0 – произвольное положительное число,
то условия определения 3 выполня -ются
для последовательности
;
значит,
![]() .
.
Докажем утверждение
2). Пусть
0 – некоторое положительное число;
обозначим:
![]() .
Так как
,
то существует
.
Так как
,
то существует
![]() такое, что
такое, что
![]() ; отсюда :
; отсюда :
![]() .
Значит, если положить
.
Значит, если положить
![]() ,
будем иметь
,
будем иметь
![]() .
Так как здесь ε - произвольное
положительное число, то последовательность
удовлет- воряет определению 1 ,п. 3.4.,
т.е.
.
.
Так как здесь ε - произвольное
положительное число, то последовательность
удовлет- воряет определению 1 ,п. 3.4.,
т.е.
.
Приведенные ниже утверждения касаются арифметических действий с б.б. последовательностями.
а) Если
![]() и
и
![]() ,
то и
,
то и
![]() (здесь следует выби- рать либо везде
знак ““,
либо везде знак “–”).
(здесь следует выби- рать либо везде
знак ““,
либо везде знак “–”).
б) Если
![]() ,
–
или ,
а последовательность
ограничена, то
,
–
или ,
а последовательность
ограничена, то
![]() стремится к ,
–
или
соответственно.
стремится к ,
–
или
соответственно.
в) Если
![]() ,
,
то и
,
,
то и
![]() .
.
г) Если
,
а
![]() ,
a
0, то
.
,
a
0, то
.
Упражнение. Доказать утверждения а) – г).
3.8. Фундаментальные последовательности
Определение
1. Последовательность
назовем фундаментальной
пос- ледовательностью, если для любого
0 существует натуральное
такое, что нера- венство
![]() справедливо при любых натуральных n
и m,
больших, чем
,
т.е. если
справедливо при любых натуральных n
и m,
больших, чем
,
т.е. если
![]() N
:
N
:
![]() N
N
![]() N
(
N
(
![]() )
)
Геометрически
сформулированные выше условия означают,
что все члены ос-татка
![]() последовательности
лежат на интервале длины 2,
в каче- стве которого можно взять
-окрестность
любой точки
последовательности
лежат на интервале длины 2,
в каче- стве которого можно взять
-окрестность
любой точки
![]() ,
где
,
где
![]() .
Такой интервал длины 2
содержит бесконечное множество членов
последовательности
,
в то время как вне этого интервала может
находиться разве лишь конечное их
количество. Существенно, что сказанное
остается справедливым при любом
0, которое может быть взято как угодно
малым. В п. 3.2. были отмечены аналогичные
черты в поведе- нии сходящейся
последовательности. Наличие этой
аналогии обьясняет следующая теорема.
.
Такой интервал длины 2
содержит бесконечное множество членов
последовательности
,
в то время как вне этого интервала может
находиться разве лишь конечное их
количество. Существенно, что сказанное
остается справедливым при любом
0, которое может быть взято как угодно
малым. В п. 3.2. были отмечены аналогичные
черты в поведе- нии сходящейся
последовательности. Наличие этой
аналогии обьясняет следующая теорема.
Теорема 1. (Критерий Kоши). Для того, чтобы последовательность была схо- дящейся, необходимо и достаточно, чтобы она была фундаментальной.
Доказательство этой теоремы мы здесь приводить не будем. Его можно найти в учебниках математического анализа [1] и [2].
Приведем пример применения критерия Коши.
Пример 1.
Пусть
![]() – заданное число,
,
.
Рассмотрим последовательность
.
Выше (п. 3.2., пример 1 ) было показано, что
при
– заданное число,
,
.
Рассмотрим последовательность
.
Выше (п. 3.2., пример 1 ) было показано, что
при
![]()
![]() .
При
.
При
![]() все члены этой последовательности равны
единице; поэтому
все члены этой последовательности равны
единице; поэтому
![]() .
При
.
При
![]() эта последовательность расходится (п.
3.2., пример 3). Таким образом, поведение
эта последовательность расходится (п.
3.2., пример 3). Таким образом, поведение
![]() известно при всяком q,
| q
|
1.
известно при всяком q,
| q
|
1.
Пусть теперь
![]() .
Покажем, что в этом случае последовательность
,
расходится. В силу критерия Коши
достаточно показать, что она не является.
фундаментальной. При произвольных
натуральных n
и m,
удовлетворяющих нера- венству n
m ,
имеем:
.
Покажем, что в этом случае последовательность
,
расходится. В силу критерия Коши
достаточно показать, что она не является.
фундаментальной. При произвольных
натуральных n
и m,
удовлетворяющих нера- венству n
m ,
имеем:
![]() .
.
Выберем
достаточно малым:
![]() .
Тогда из полученных выше не- равенств
при любых натуральных n
и m
будем иметь:
.
Тогда из полученных выше не- равенств
при любых натуральных n
и m
будем иметь:
![]() .
Следовательно, для такого
.
Следовательно, для такого
![]() не существует натуральное k
ε,
о
котором
идет речь в определении 1; по- этому
последовательность
,
,
не является фундаментальной (см. также
п. 3.7.,пример 1 ). В силу критерия Коши она
расходится.
не существует натуральное k
ε,
о
котором
идет речь в определении 1; по- этому
последовательность
,
,
не является фундаментальной (см. также
п. 3.7.,пример 1 ). В силу критерия Коши она
расходится.
