
§ 3. Предел последовательности чисел
Последовательности вещественных чисел
Мы будем рассматривать
здесь бесконечные последовательности
вещественных чисел. Бесконечную
последовательность х![]() ,
х
,
х![]() ,
… , х
,
… , х![]() ,
… будем обозначать через
,
… будем обозначать через
![]() , иногда через
, иногда через
![]() .
Числа х
,
образующие последовательность, называют
членами этой последовательности. Эти
числа не обязательно все попарно
различны, некоторые из членов
последовательности с разными номерами
могут быть одинаковы- ми числами.
Возможен и такой случай, когда все члены
последовательности равны одному и тому
же числу ; такие последовательности
называют стационарными.
.
Числа х
,
образующие последовательность, называют
членами этой последовательности. Эти
числа не обязательно все попарно
различны, некоторые из членов
последовательности с разными номерами
могут быть одинаковы- ми числами.
Возможен и такой случай, когда все члены
последовательности равны одному и тому
же числу ; такие последовательности
называют стационарными.
Последовательность называют ограниченной сверху (ограниченной снизу), если существует число М такое, что все члены последовательности не больше (не меньше ) числа М. Последовательность называют ограниченной, если она ограничена и сверху, и снизу.
Последовательность
{x
k}
называют возрастающей
( убывающей)
последова- тельностью, если при всех k
N
справедливо
![]() (
(![]() ).
).
Последовательность
называют неубывающей
(невозрастающей)
последо- вательностью, если при всех k
N
справедливо
![]() (
(![]() ).
).
Последовательности неубывающие и невозрастающие называют монотонными последовательностями. Те из монотонных последовательностей, которые возрастают или убывают, называют строго монотонными.
Пусть задана
последовательность {x
k}
и пусть n
– некоторое натуральльное число.
Бесконечную последовательность
![]() ,
,
![]() ,
,
,
,
![]() ,
назовем остатком
последовательности
,
назовем остатком
последовательности
![]() и обозначим через
и обозначим через
![]() .
Остаток последовательности – это
бесконечная последовательность,
полученная в результате отбрасывания
некото- рого конечного количества первых
членов исходной последовательности
.
Остаток последовательности – это
бесконечная последовательность,
полученная в результате отбрасывания
некото- рого конечного количества первых
членов исходной последовательности
3.2. Сходящиеся и расходящиеся последовательности
Пусть задана
некоторая последовательность
![]() и пусть a
– некоторое число, т.е. a
R.
и пусть a
– некоторое число, т.е. a
R.
Определение 1.
Число a
называют пределом последовательности
![]() ,
если для любого положительного числа
существует натуральное
,
если для любого положительного числа
существует натуральное
![]() такое,
что все члены последовательности
такое,
что все члены последовательности
![]() ,
номера k
которых превышают
,
удовлетворяют неравенству
,
номера k
которых превышают
,
удовлетворяют неравенству
![]() .
.
Ниже мы часто будем прибегать к следующей компактной записи условия определения 1:
>
0
![]() k
N
k
N
![]() .
.
Эту строчку можно
прочесть так : для любого положительного
ε существует натуральное
такое,
что при всех натуральных k
, удовлетворяющих неравенству
![]() ,
справедливо неравенство
,
справедливо неравенство
![]()
Если a
удовлетворяет этому определению, то
будем записывать а
![]() или
или
![]() и будем говорить, что последовательность
стремится к a
или сходится к a
и будем говорить, что последовательность
стремится к a
или сходится к a
Пусть a – некоторое число, а ε – некоторое положительное число. Введем тер- мины: окрестность точки а и ε - οкрестность точки a.
Окрестностью
точки а
будем
называть всякий интервал, содержащий
эту точ- ку; обозначать окрестность
точки a
будем символом
![]() .
.
-окрестностью
точки a
назовем интервал
![]() ;
обозначать ε - окрестность точки а
будем
символом
;
обозначать ε - окрестность точки а
будем
символом
![]() .
.
Заметим:
![]()
![]() .
Из определения 1 вытекает: если
.
Из определения 1 вытекает: если
![]() ,
то в -
окрестности числа a
лежит бесконечное множество членов
после- довательности, а именно, в
лежат все те
,
то в -
окрестности числа a
лежит бесконечное множество членов
после- довательности, а именно, в
лежат все те
![]() ,
номера k
которых превышают
:
,
номера k
которых превышают
:
![]()
.
Существенно, что это остается
справедливым при любом, сколь угодно
малом
0: как бы мало ни было
0, в
содержится бесконеч- ное множество
членов последовательности. Существенно
также и то , что вне -
ок- рестности может находиться разве
лишь конечное множество членов
последовательно- сти, ибо в определении
1 не содержится никаких требований к
конечному множеству
.
Существенно, что это остается
справедливым при любом, сколь угодно
малом
0: как бы мало ни было
0, в
содержится бесконеч- ное множество
членов последовательности. Существенно
также и то , что вне -
ок- рестности может находиться разве
лишь конечное множество членов
последовательно- сти, ибо в определении
1 не содержится никаких требований к
конечному множеству
![]() первых
членов последовательности, значит,
только они и могут оказаться вне
.
первых
членов последовательности, значит,
только они и могут оказаться вне
.
Геометрически
величина
![]() есть расстояние между точками числовой
оси, изображающими числа
и a;
поэтому геометрический смысл определения
1 можно передать фразой: при неограниченном
увеличении номера k
точка
есть расстояние между точками числовой
оси, изображающими числа
и a;
поэтому геометрический смысл определения
1 можно передать фразой: при неограниченном
увеличении номера k
точка
![]() неог- раниченно приближается к точке
a.
неог- раниченно приближается к точке
a.
Пример 1.
Пусть q,
![]() – заданное число. Рассмотрим
геометрическую прогрессию 1, q,
q
– заданное число. Рассмотрим
геометрическую прогрессию 1, q,
q![]() ,
… , q
,
… , q![]() ,
…, т.е. последовательность
,
…, т.е. последовательность
![]() ,
где
,
где
![]() ,
и дока- жем, что ее пределом является а
= 0.
,
и дока- жем, что ее пределом является а
= 0.
![]() Нам предстоит
проверить для последовательности
и числа a
0 выполнение условий определения 1:
Нам предстоит
проверить для последовательности
и числа a
0 выполнение условий определения 1:
0
k
N
![]() .
.
Неравенство
![]() равносильно неравенству
равносильно неравенству
![]() .
Прологарифмировав, получим:
.
Прологарифмировав, получим:
![]() ;
поделив обе части последнего неравенства
на отрицательное число
;
поделив обе части последнего неравенства
на отрицательное число
![]() ,
получим равносильное неравенство
,
получим равносильное неравенство
![]() .
Существует бесконечно много натуральных
чисел, превышающих вещественное число
.
Существует бесконечно много натуральных
чисел, превышающих вещественное число
![]() .
Выберем какое-нибудь из них и назовём
его
.
Тогда для всякого натурального
.
Выберем какое-нибудь из них и назовём
его
.
Тогда для всякого натурального
![]() такого, что
такого, что
![]() справедливо
и, следовательно, справедливо
справедливо
и, следовательно, справедливо
![]() .
Таким образом,
.
Таким образом,
![]()
![]() .
.
Итак, для любого
0 существует натуральное
такое, что при всех
справедливо
.
Тем самым доказано :
![]() .
Заметим: на роль
может быть выбрано любое натуральное
число, большее, чем
.
.
Заметим: на роль
может быть выбрано любое натуральное
число, большее, чем
.
![]()
Последовательность, имеющую предел, называют сходящейся последовательно- стью. Далеко не всякая последовательность является сходящейся.
Пример 2.
Рассмотрим
последовательность чисел натурального
ряда, т.е. последовательность![]() ,
где
,
где
![]() ,
k
N.
Покажем, что эта последовательность не
имеет предела и, следовательно, сходящейся
не является.
,
k
N.
Покажем, что эта последовательность не
имеет предела и, следовательно, сходящейся
не является.
Пусть a
– некоторое вещественное число. Положим
![]() .
Если бы a
было пределом рассматриваемой
последовательности, то в -окрестности
,
т.е. на интервале
.
Если бы a
было пределом рассматриваемой
последовательности, то в -окрестности
,
т.е. на интервале![]() содержалось бы бесконечное множество
её членов, т.е. на- туральных чисел.
Очевидно, однако, что на интервале
,
длина которого равна единице, может
содержаться не более одного натурального
числа. Значит, при
в
содержится не более одного члена
рассматриваемой последователь – ности;
поэтому a
не может быть её пределом. Но в этих
рассуждениях a
– произволь- ное вещественное число.
Следовательно, ни одно вещественное
число не может быть пределом
последовательности чисел натурального
ряда.
содержалось бы бесконечное множество
её членов, т.е. на- туральных чисел.
Очевидно, однако, что на интервале
,
длина которого равна единице, может
содержаться не более одного натурального
числа. Значит, при
в
содержится не более одного члена
рассматриваемой последователь – ности;
поэтому a
не может быть её пределом. Но в этих
рассуждениях a
– произволь- ное вещественное число.
Следовательно, ни одно вещественное
число не может быть пределом
последовательности чисел натурального
ряда.
Пример 3.
Рассмотрим последовательность
![]() ,
где
,
где
![]() ,
т.е.
,
т.е.
![]() при нечетных k
и
при нечетных k
и
![]() при четных k.
Покажем, что эта последовательность к
схо- дящимся не принадлежит.
при четных k.
Покажем, что эта последовательность к
схо- дящимся не принадлежит.
Действительно,
пусть сначала a
1.
Очевидно, что для такого a
всегда можно подобрать
0 так, чтобы -окрестность
не содержала точек 1
и –1. Таким образом, в указанной окрестности
нет членов рассматриваемой последова-
тельности, поэтому такое a
не может быть ее пределом. Пусть теперь
![]() .
Положим
.
Тогда -окрестность
точки а
представляет собой интервал
.
Положим
.
Тогда -окрестность
точки а
представляет собой интервал
![]() .
Число –1 лежит вне этого интервала.
Значит, вне указанной -окрестности
лежит бесконечное множество членов
последовательности, а именно, все
,
у которых индекс k
четный . Значит,
не может быть пределом: если
было бы пределом рассматривае- мой
последовательности, то вне ε – окрестности
этой точки находилось бы разве лишь
конечное множество ее членов.
.
Число –1 лежит вне этого интервала.
Значит, вне указанной -окрестности
лежит бесконечное множество членов
последовательности, а именно, все
,
у которых индекс k
четный . Значит,
не может быть пределом: если
было бы пределом рассматривае- мой
последовательности, то вне ε – окрестности
этой точки находилось бы разве лишь
конечное множество ее членов.
Аналогично можно показать, что и a –1 пределом этой последовательности не является.
Последовательность, не имеющую предела, называют расходящейся последова- тельностью.
.3.3.. Некоторые теоремы о сходящихся последовательностях
Теорема 1. ( О единственности предела ) Если последовательность имеет предел, то только один.
Пусть последовательность сходится к a, a R. Покажем, что всякое отличное от а число не может быть ее пределом .
Рис.
3.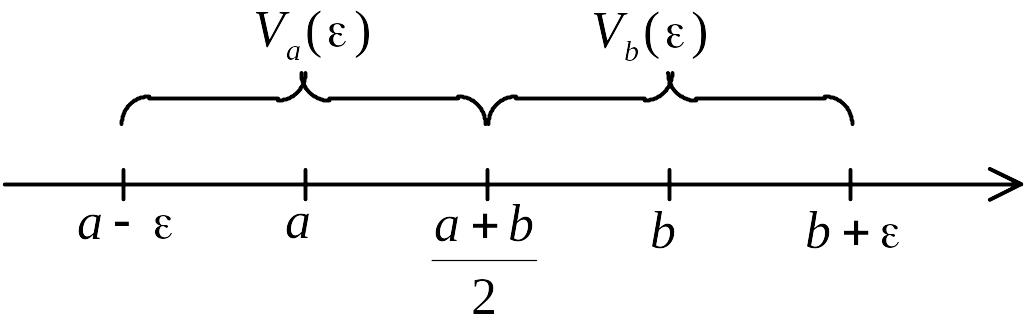
![]() ,
т.е.
– полови- на расстояния между точками
a и b.
Заметим, что -окрестности
,
т.е.
– полови- на расстояния между точками
a и b.
Заметим, что -окрестности
![]() и
и
![]() не пересекаются ( рис.3.). Так как
,
для указанного
найдется натураль- ное
не пересекаются ( рис.3.). Так как
,
для указанного
найдется натураль- ное
![]() такое, что при всех
такое, что при всех
![]() выполняется неравенство
выполняется неравенство
![]() .
Это означает, что -
окрестности
принадлежат все те члены
пос- ледовательности, номера которых
превышают
,
а не принадлежать
могут только
.
Это означает, что -
окрестности
принадлежат все те члены
пос- ледовательности, номера которых
превышают
,
а не принадлежать
могут только
![]() ,
,
![]() ,
,
,
,
![]() .
Следовательно, только эти члены
последовательности могут оказаться в
.
Итак, в
- окрестности точки b
содержится разве лишь конечное множество
членов последовательности
.
Следовательно, только эти члены
последовательности могут оказаться в
.
Итак, в
- окрестности точки b
содержится разве лишь конечное множество
членов последовательности
![]() ,
поэтому число b
не является ее преде- лом.
,
поэтому число b
не является ее преде- лом.
Теорема 2. ( Об ограниченности сходящейся последовательности ) Если после- довательность сходится, то она ограничена.
Пусть
последовательность
![]() сходится:
сходится:
![]() a.
Положим
1. По определению 1 найдется натуральное
a.
Положим
1. По определению 1 найдется натуральное
![]() такое, что
такое, что
![]() при всех
при всех
![]() .
Это значит, что все члены последовательности,
номера которых превышают
,
лежат на интервале
.
Это значит, что все члены последовательности,
номера которых превышают
,
лежат на интервале
![]() ;
вне этого интервала могут оказаться
лишь числа
,
,,
;
вне этого интервала могут оказаться
лишь числа
,
,,![]() .
.
Обозначим через
![]() и
и
![]() соответственно наименьшее и наибольшее
из чисел
,
,
,
соответственно наименьшее и наибольшее
из чисел
,
,
,![]() ,
и пусть
,
и пусть
![]() ,
,
![]() .
Очевидно, все члены
.
Очевидно, все члены
![]() последовательности
не меньше A
и не больше B,
т.е. последовательность
ограничена.
последовательности
не меньше A
и не больше B,
т.е. последовательность
ограничена.
Замечание 1. Из сходимости последовательности вытекает ее ограниченность. Обратное, вообще говоря, неверно: ограниченная последовательность не обязательно сходится (см. пример 3).
Теорема 3. (
О стабилизации знака неравенства )
Пусть
последовательность
сходится к a,
a
R,
и пусть p
– некоторое число, p
a
(p
a).
Тогда существу- ет
![]() такое, что при всех
такое, что при всех
![]() справедливо неравенство
справедливо неравенство
![]() (
(
![]() ).
).
Пусть p
a.
Положим
a
– p.
В силу определения 1 для этого
найдется
![]() такое, что
такое, что
![]() ,
т.е. при любых
,
число
,
т.е. при любых
,
число
![]() удовлетворя- ет неравенствам
удовлетворя- ет неравенствам
![]() .
Но a
–
a
– (a
– p)
p,
значит,
.
Положим
.
Но a
–
a
– (a
– p)
p,
значит,
.
Положим
![]() .
Тогда при всех
справедливо
.
.
Тогда при всех
справедливо
.
В случае p a доказательство аналогично.
Теорема 4. (
О предельном
переходе в неравенстве )
Пусть последовательность
сходится к a,
а последовательность
![]() сходится к b.
Если при всех нату- ральных k
имеют место неравенства
сходится к b.
Если при всех нату- ральных k
имеют место неравенства
![]() ,
то и a
b.
,
то и a
b.
Рассуждаем “от
противного” : допустим, что a
b.
Обозначим:
![]() ,
т.е. p
есть середина отрезка с концами a
и b
: b < p
< а
. Так как p
a,
по теореме 3 существует число
,
т.е. p
есть середина отрезка с концами a
и b
: b < p
< а
. Так как p
a,
по теореме 3 существует число
![]() такое, что при всех
такое, что при всех
![]() справедливо
справедливо
![]() .
Так как p
b,
по той же теореме существует
.
Так как p
b,
по той же теореме существует![]() такое,
что при всех
такое,
что при всех
![]() выпол- няется неравенство
выпол- няется неравенство
![]() .
Обозначим:
.
Обозначим:
![]() .
Пусть натуральное число k
удовлетворяет условию
.
Тогда
,
и потому
.
С другой стороны, для такого k
выполнено и условие
,
и потому
.
Пусть натуральное число k
удовлетворяет условию
.
Тогда
,
и потому
.
С другой стороны, для такого k
выполнено и условие
,
и потому
![]() .
Значит, при
,
имеем
.
Значит, при
,
имеем
![]() ,
т.е.
,
т.е.
![]() ,
а это противоречит условию теоремы (
при всех k
N).
Противоречие возникло из-за допущения
a
b,
поэтому a
b.
,
а это противоречит условию теоремы (
при всех k
N).
Противоречие возникло из-за допущения
a
b,
поэтому a
b.
Следствие. Пусть все члены последовательность не больше(не меньше) некоторого числа b . если эта последовательность сходится, то её предел также не боль- ше (не меньше) b .
► Пусть при всех
k
N
![]() и
пусть
и
пусть
![]() .
Введём в рассмотрение стаци- онарную
последовательность
.
Введём в рассмотрение стаци- онарную
последовательность
![]() ,
каждый член которой равен b.
Очевидно,
,
каждый член которой равен b.
Очевидно,
![]() Имеем: при всех
Имеем: при всех
![]() N
,
т.е.
N
,
т.е.
![]() .
Применив теорему 4, получим:
.
Применив теорему 4, получим:
![]() .
Доказательство неравенства
.
Доказательство неравенства
![]() в случае
в случае
![]() проводится аналогично. ◄
проводится аналогично. ◄
Замечание
2. Если при
всех
N
имеют место строгие неравенства
![]() ,
то, вообще говоря, для пределов а
и b
отсюда не следует строгое неравенство
,
то, вообще говоря, для пределов а
и b
отсюда не следует строгое неравенство
![]() ,
т.е. возможно и
,
и равенство а
= b.
Действительно, пусть, например,
,
т.е. возможно и
,
и равенство а
= b.
Действительно, пусть, например,
![]() ,
,
![]() ,
где
,
где
![]() .
Тогда при всех
.
Тогда при всех
![]()
![]() ,
но
,
но
![]() .
.
Теорема 5. (
О “ сжатой
“ последовательности ) Пусть
заданы три после- довательности
,
![]() ,
,
![]() ,
причем выполнены следующие условия:
,
причем выполнены следующие условия:
1) при всех k
N
![]() ,
и 2)
,
и 2)
![]() ,
a
R.
,
a
R.
Тогда последовательность
![]() сходится, а ее предел равен a.
сходится, а ее предел равен a.
Нужно показать,
что для последовательности
и числа a
выполнены условия определения 1:
![]() N:
N:
![]() N
N
![]()
Пусть
– заданное положительное число. Так
как
![]() ,
существует нату- ральное
,
существует нату- ральное
![]() такое, что при всех
такое, что при всех
![]() выполняется
выполняется
![]() ,
т.е.
,
т.е.
![]() .
(1)
.
(1)
Так как
![]() ,
существует
,
существует
![]() такое, что при всех
такое, что при всех
![]() выполняется
выполняется
![]() ,
т.е.,
,
т.е.,
![]() .
(2)
.
(2)
Обозначим:
![]() .
Пусть k
– натуральное число, большее, чем
.
Из
следует
и
.
Так как
,
для числа
выполняется (1); т.к.
,
для числа
.
Пусть k
– натуральное число, большее, чем
.
Из
следует
и
.
Так как
,
для числа
выполняется (1); т.к.
,
для числа
![]() справедливо (2); кроме того, в силу условия
1) теоремы имеем
.
Отсюда следует:
справедливо (2); кроме того, в силу условия
1) теоремы имеем
.
Отсюда следует:
![]()
Значит, можно
записать:
![]() ,
т.е.
,
т.е.
![]() .
Так как здесь
– произвольное положительное число,
то мы показали, что
0
.
Так как здесь
– произвольное положительное число,
то мы показали, что
0
![]() k
N
k
N
![]() ;
значит,
;
значит,
![]() .
.
Теорема 6. Пусть – заданная последовательность, а n – некоторое натуральное число. Тогда:
1. Если
![]() сходится к числу a,
то и остаток последовательности
сходится к числу a,
то и остаток последовательности![]() имеет тот же предел.
имеет тот же предел.
2. Если расходится, то и остаток является расходящейся последовательностью.
Упражнение. Доказать утверждения 1. и 2 . теоремы 6.
3.4. Бесконечно малые последовательности
Определение 1.
Последовательность
![]() будем называть
бесконечно малой
последовательностью (б.м.последовательностью),
если она сходится, а ее предел равен
нулю, т.е.
будем называть
бесконечно малой
последовательностью (б.м.последовательностью),
если она сходится, а ее предел равен
нулю, т.е.
![]() N
N
![]() N
N
![]()
Б.м.последовательностью
является, например, последовательность
![]() ,
рас- смотренная в примере 1, п. 3.2.
,
рас- смотренная в примере 1, п. 3.2.
Пусть заданы
последовательности
и
Последовательности
![]() и
и
![]() будем называть суммой и произведением
последовательностей
будем называть суммой и произведением
последовательностей
![]() и
и
![]() соответственно. Если
соответственно. Если
![]() при всех k
N,
то последовательность
при всех k
N,
то последовательность
![]() назо- вем частным последовательностей
и
.
назо- вем частным последовательностей
и
.
Теорема 1. (О сумме б.м. последовательностей ) Сумма б.м. последова- тельностей является б.м. последовательностью.
Пусть
![]() и
и
![]() есть б.м. последовательности. Положим
есть б.м. последовательности. Положим
![]()
![]() и рассмотрим последовательность
и рассмотрим последовательность
![]() .
.
Пусть
0 – заданное число. Тогда и
![]() .
Так как
.
Так как
![]() ,
то сущест- вует
,
то сущест- вует
![]() такое, что
такое, что
![]()
![]() .
Так как
.
Так как
![]() ,
то существует
,
то существует
![]() такое, что
такое, что
![]()
![]() .
Обозначим:
.
Обозначим:
![]() .
При
.
При
![]() имеем :
имеем :
![]() .
.
Таким образом, для
всякого
0 существует
такое, что при всех
выполняется
![]() .
Значит,
.
Значит,
![]() .
.
Замечание1.
Пусть n
≥ 2, и пусть каждая из последовательностей
![]()
![]()
![]() является бесконечно малой. Тогда
последовательность
,
где
является бесконечно малой. Тогда
последовательность
,
где
![]() .
также является б.м. последовательностью
. Доказательство этого утверждения
аналогично доказательству теоремы 1.
.
также является б.м. последовательностью
. Доказательство этого утверждения
аналогично доказательству теоремы 1.
Теорема 2. ( О произведении б.м. и ограниченной последовательностей ) Произведение б.м. последовательности и ограниченной последовательности есть б.м. последовательность.
Пусть
заданы последовательности
и
,
причём
ограни- чена, а
-бесконечно малая. Так как
ограничена,
то существует число M
0 такое, что при всех натуральных k
справедливо неравенство
![]() Пусть
0 – некоторое заданное число. Так как
Пусть
0 – некоторое заданное число. Так как
![]() ,
найдется
такое, что
,
найдется
такое, что
![]() .
Отсюда получаем: при любых натуральных
,
превышающих
.
Отсюда получаем: при любых натуральных
,
превышающих
![]() ,
спра- ведливо
,
спра- ведливо
![]()
![]()
![]() .
Таким образом,
.
Таким образом,
.
> 0
k
N
![]() .
.
Значит, .
Следствие.
Пусть a
– некоторое число, а
– б.м. последователь- ность. Тогда
![]() ,
где
,
где
![]() ,
есть б.м. последовательность.
,
есть б.м. последовательность.
Это утверждение
вытекает из доказанной теоремы :
достаточно в качестве
взять стационарную последовательность,
положив
![]() .
.
Упражнение. Доказать, что произведение б.м. последовательностей есть б.м. последовательность.
Теорема 3. (О разности между последовательностью и числом )
Пусть - некоторая последовательность , a - некоторое число. Обозначим : α k = x k – a . Для того чтобы число a было пределом последовательности , необходимо и достаточно, чтобы последовательность была бесконечно малой.
Утверждение
теоремы можно записать так: (![]() )
(
).
)
(
).
означает:
0
k
N
![]() ;
(3)
;
(3)
означает:
0
k
N
![]() .
(4)
.
(4)
Но
![]() .
Если выполняется (3), то, заменив в (3)
.
Если выполняется (3), то, заменив в (3)
![]() на
на
![]() ,
получаем (4); таким образом, (3)
(4). Если выполняется (4), то, заменив в
(4)
на
,
получим (3); таким образом, (4)
(3). Итак, (3)
(4), что и требовалось доказать.
,
получаем (4); таким образом, (3)
(4). Если выполняется (4), то, заменив в
(4)
на
,
получим (3); таким образом, (4)
(3). Итак, (3)
(4), что и требовалось доказать.
Замечание
2. Утверждение
теоремы 3 можно сформулировать несколько
ина- че: для того чтобы
,
необходимо и достаточно, чтобы
можно было представить в виде суммы:
х
=![]() ,
где
.
В такой формулировке эта теорема
использована в следующем примере.
,
где
.
В такой формулировке эта теорема
использована в следующем примере.
Пример 1. Пусть
a
R,
a
1. Тогда
![]() .
.
Положим
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Имеем:
.
Имеем:
![]() ,
отсю- да :
,
отсю- да :
![]() .
Воспользуемся неравенством Бернулли
(п. 2.5 пример 1) :
.
Воспользуемся неравенством Бернулли
(п. 2.5 пример 1) :
![]() .
.
![]() .
Очевидно,
.
Очевидно,
![]() .
Отсюда:
.
Отсюда:
![]() и, значит,
и, значит,
![]() .
Положим:
.
Положим:
![]() ,
,
![]() ,
,
![]() ,
и рассмотрим последовательности
,
,
и
,
и рассмотрим последовательности
,
,
и
![]() .
Имеем: 1)
.
Имеем: 1)
![]() при всех k
N
и 2)
при всех k
N
и 2)
![]() ,
,
![]() .
По теореме о “ cжатой
“ последовательности ( п. 3.3. теорема
5)
.
По теореме о “ cжатой
“ последовательности ( п. 3.3. теорема
5)
![]() ,
т.е.
.
Итак,
,
где
.
Значит,
,
т.е.
.
Итак,
,
где
.
Значит,
![]() .
.
