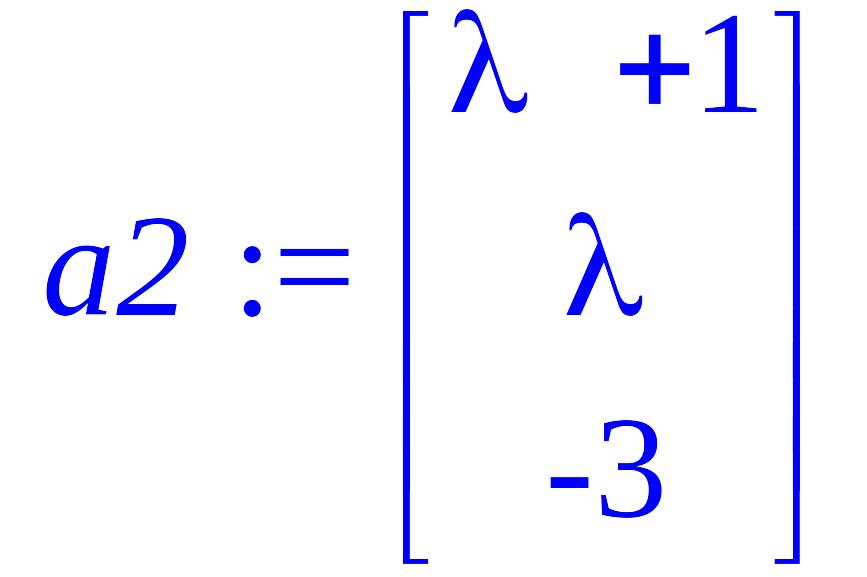Задание 2.
Даны матрицы:
,
,
.
Найти: (AB)C , detA, detB, detC,
det[(AB)C]. Наберите:
> with(linalg):restart;
> A:=matrix([[4,3],[7,5]]):
> B:=matrix([[-28,93],[38,-126]]):
> C:=matrix([[7,3],[2,1]]):
> F:=evalm(A&*B&*C);
> Det(A)=det(A); Det(B)=det(B); Det(C)=det(C);
Det(F)=det(F);
Det(A)= 1
Det(B)= 6
Det(C)=1
Det(F)=6
Дана матрица
,
найти: detA,
,
A’, det(M22). Наберите:
> A:=matrix([[2,5,7],[6,3,4],[5,-2,-3]]);
> Det(A)=det(A);
Det(A)= 1
> transpose(A);
> inverse(A);
> det(minor(A,2,2));
41
Найти ранг матрицы
.
> A:=matrix([[8,-4,5,5,9], [1,-3,-5,0,-7],
[7,-5,1,4,1], [3,-1,3,2,5]]):
> r(A)=rank(A);
r(A)=3
Вычислить
,
где
.
> exponential([[3,-1],[1,1]]);
Дана матрица
.
Найти значение многочлена
.
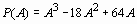> A:=matrix([[5,1,4],[3,3,2],[6,2,10]]):
> P(A)=evalm(A^3-18*A^2+64*A);
§ 3. Описание пакета LinearAlgebra
В Maple имеется пакет LinearAlgebra, ориентированный на решение задач линейной (матричной) алгебры. Он загружается соответствующей командой:
[> with(LinearAlgebra);
После выполнения этих команд система выводит на экран список процедур и функций, которыми располагает пакет LinearAlgebra.
Пакет LinearAlgebra
является более мощным и совершенным по
сравнению с linalg
(в ранних версиях программы). Он
предназначен для работы с матрицами и
векторами больших размеров. Самым
простым образом матрицу
размером
в пакете LinearAlgebra
можно сформировать при помощи команды
[> Matrix(m, n, [[a[1,1],…,a[1,n]],…,[a[m,1],…,a[m,n]]]);
Приведем в табл. 3.1 назначение наиболее часто применимых процедур и функций пакета LinearAlgebra. Более полную информацию о каждой процедуре или функции можно узнать в справке, или набрав команду
[> help(имя_процедуры);
Таблица 3.1.
Название процедуры, функции |
Формат команды |
Назначение процедуры, функции |
Matrix |
[> Matrix(m, n, [[a[1,1],…,a[1,n]],…,[a[m,1],…,a[m,n]]]); |
Формирование матрицы |
Basis |
|
Определяет базис для векторного пространства, заданного системой векторов |
CharacteristicMatrix |
|
Создает для квадратной матрицы ее характеристическую матрицу |
CharacteristicPolynomial |
|
Создает для квадратной матрицы ее характеристический многочлен |
Determinant |
|
Вычисляет для квадратной матрицы ее определитель |
DiagonalMatrix |
|
Создает диагональную матрицу |
Eigenvalues |
|
Вычисляет для квадратной матрицы ее собственные значения (собственные числа) |
Eigenvectors |
|
Вычисляет для квадратной матрицы ее собственные векторы (рекомендуется использовать вместе с процедурой Eigenvalues) |
LinearSolve |
|
Решает систему линейных алгебраических уравнений (СЛАУ) в матричной форме |
MatrixAdd |
|
Процедура сложения двух матриц |
Matrixlnverse |
|
Процедура нахождения обратной матрицы |
MatrixMatrixMultiply |
|
Процедура произведения двух матриц |
MatrixNorm |
|
Функция вычисления нормы матрицы |
MatrixScalarMultiply |
|
Процедура умножения матрицы на скаляр |
MatrixVectorMultiply |
|
Процедура умножения матрицы на вектор |
Minor |
|
Вычисляет минор матрицы |
Normalize |
|
Нормализует вектор |
NullSpace |
|
Возвращает нуль-пространство (ядро) матрицы |
Rank |
|
Вычисляет ранг матрицы |
SylvesterMatrix |
|
Конструирует матрицу Сильвестра из многочленов |
Transpose |
|
Вычисляет матрицу, транспонированную к данной |
Пример 3.1. Исследовать СЛАУ
с параметром
(СЛАУ задана своей расширенной матрицей)
и решить в каждом случае:
.
Ниже приведен текст рабочего листа по решению данной задачи (с описаниями по ходу выполнения команд).
[> restart; with(LinearAlgebra): /задаем вектор-столбцы основной матрицы/ [> a1:=Vector([2,1,3]); a2:=Vector([lambda+1,lambda,-3]); a3:=Vector([lambda-2,-3,-7]);
/задаем основную матрицу и вектор-столбец свободных коэффициентов системы/ [> A:=Matrix(3,3,[a1,a2,a3]); B:=Vector([3,lambda+2,3]);
/выводим определитель основной матрицы системы, решение системы в матричном виде (при значениях, в которых определитель основной матрицы не равен нулю)/ [> Delta:=Determinant(A); X:=LinearSolve(A,B);
/вычисляем
значения параметра
[> Korni:=solve(Determinant(A)=0);
[> lambda:=Korni[1]; X:=LinearSolve(A,B);
Error,(in LinearAlgebra:-LA_Main:-LinearSolve) inconsistent system /Maple предупреждает, что СЛАУ при данном значении параметра несовместна/ [> lambda:=Korni[2]; X:=LinearSolve(A,B);
/СЛАУ
имеет бесконечное множество решений
при этом значении параметра
|
,
при котором определитель обращается
в нуль/
/
Пример 3.2. Найти собственные числа и соответственные собственные векторы матрицы
.
Текст рабочего листа по решению задачи имеет вид:
[> restart; with(LinearAlgebra): [> A:=Matrix(3,3,[[3,-6,9],[1,-2,3],[-3,6,-9]]); /задание исходной матрицы/
[> Add(A,-lambda): p(lambda):=Determinant(Add(A,-lambda));
/составление
характеристического многочлена
[> solve(p(lambda)=0,{lambda}); /вычисление собственных чисел матрицы/
[> v:=Eigenvalues(A); F:=Eigenvectors(A); /вычисление собственных чисел и собственных векторов матрицы с помощью процедуры Eigenvectors: первый столбец v – собственные числа матрицы, вторая матрица F содержит соответствующие собственные векторы матрицы, они расположены по столбцам!)/
|
матрицы/
Тема: Матричные уравнения
Задание:
Решить матричное уравнение АХ=ХВ для заданных матриц А и В
Алгоритм:
Построить ЖНФ для А и В
найти элементарные делители
построить Жорданов базис
составить Жорданову фору
составить матрицу перехода
2. определить стуктуру блочной матрицы
3.
Встроенные функции MAPLE
restart:with(linalg):
(ввод матрицы A)
A:=matrix([[-17,25,-7,-12,-2,-5,-22],[-9,12,4 и т.д. по строкам]]);
(построение характеристического полинома)
charpoly(A,lambda);
(нахождение собственных значений)
lambda:=eigenvals(A);
(построение характеристической матрицы)
E:=diag(1,1,1,1,1,1,1):
B1:=evalm(A-lambda[1]*E);
(резервируем вектор для собственного вектора)
C:=vector(7,0):
Решаем систему B1*X=0, решение - собственный вектор e1.
> e1:=linsolve(B1,C);
Используем найденный базисный вектор e1 как первый столбец матрицы перехода S.
S1:=matrix(7,1,0):
for i from 1 to 7 do S1[i,1]:=subs(_t[1]=1,e1[i]); end do: evalm(S1);
Теперь обрабатываем корневое подпространство второго собственного числа, - строим его Жорданову "башню".
B2:=evalm(A-lambda[2]*E);
rank(B2); rank(B2^2); rank(B2^3); rank(B2^4); rank(B2^5); rank(B2^6);
Решаем методом Гаусса системы (B2^k)*X=0, k=1..3.
kernB23:=linsolve(B2^3,C);
kernB22:=linsolve(B2^2,C);
kernB21:=linsolve(B2,C);
M23a:=gaussjord(M23);
e4:=submatrix(M23,1..7,[6]): e3:=evalm(B2&*e4): e2:=evalm(B2&*e3): evalm(transpose(B2&*e2));
Наращиваем матрицу перехода S векторами e2, e3, e4 (снизу вверх по вертикали в башне ).
> S1_4:=concat(S1,e2,e3,e4);
Пример:
Шаблон:
Проверка: