
- •Приложение II некоторые сведения из курса «теоретическая механика» операции с векторами. Уравнение статики
- •П y роекции векторов на оси X и y.
- •Момент относительно точки.
- •Подбор уравнений статики для определения неизвестных векторов уравновешенной системы сил
- •Приложение III алгоритм определения внутренних силовых факторов в сечении плоской стержневой системы
- •Правило знаков
- •Построение эпюр внутренних усилий по характерным точкам в балке
- •Построение эпюр m, q, n
Приложение II некоторые сведения из курса «теоретическая механика» операции с векторами. Уравнение статики
Пусть внешняя нагрузка представлена в виде:
вектора силы;
вектора момента;
равномерно распределённой нагрузки.
Рассмотрим составление уравнений статики с использованием этих векторов.
П y роекции векторов на оси X и y.
Рис. П1
Будем рассматривать задачу в плоскости xy. На рис. П1,а показаны проекции вектора V на оси x и y: Vx=Vcos; Vy=Vsin.
На рис. П1,б показан вектор W, параллельный оси y. В этом случае проекция на ось y (параллельную вектору) равна величине самого вектора, а проекция на ось x равна нулю. Таким образом, вектор даёт нулевую проекцию на ось, перпендикулярную этому вектору.
На рис. П1,в показан сосредоточенный момент, который можно представить в виде пары сил равной величины и противоположного направления. Тогда проекция сосредоточенного момента на любую ось равна нулю.
Если имеет место равномерно распределённая нагрузка интенсивностью q, которая действует на длине распределения l, то эту нагрузку заменяют равно-
R=ql
действующей R
(рис. П2). Равнодействующая
представляет собой вектор-силу и
прикладывается посередине участка,
где действует распределённая нагрузка.
Величина равнодействующей равна ql.
Далее проекции на оси определяются так
же, как и для вектора-силы.
l/2
q

l

Рис. П2
Момент относительно точки.
Сосредоточенная сила создаёт момент относительно точки О, равный величине вектора, умноженной на плечо. Плечо есть кратчайшему расстоянию от точки О до вектора, т.е. это перпендикуляр, опущенный из точки О на вектор (рис. П3,a) , либо на линию действия вектора (рис. П3,б).
В случае, если точка О лежит на линии действия вектора, момент вектора силы относительно этой точки равен нулю, т.к. плечо при этом равно нулю.
Таким образом, сила создаёт нулевой момент относительно множества точек, которые лежат на линии действия вектора (рис. П3,в).
V



a)
б)
в)
V
О3
r
О2
О
Рис. П3
О1
Сосредоточенный момент М создает момент относительно точки О равный величине момента М без плеча.
В случае действия распределённой нагрузки, её заменяют равнодействующей. Далее для определения момента относительно точки О, вектор равнодействующей распределённой нагрузки умножается на плечо.
Пример 1. Дана система векторов в плоскости xy (рис. П4). Требуется составить для них уравнения статики: сумма проекций на ось x и сумма проекций на ось y.
R=q∙l
y
x
F3
l
F2
600


F1
q
M
x
Рис. П4
Решение:
![]()
![]()
Пример 2. Возьмём ту же систему векторов. Требуется cоставить для них уравнения статики: сумма моментов относительно точки О. В качестве положительного возьмём направление против хода часовой стрелки. На рис. П5 показаны все необходимые отрезки (плечи векторов).
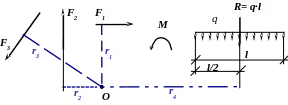
Рис. П5
Решение:
![]()
