2. Внутрішня енергія реального газу.
Знайдемо залежність внутрішньої енергії системи від об’єму та від температури.
З
основного рівняння термодинаміки для
квазістатичного процесу (формула
(*))
,
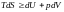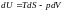де
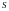це
функція стану. Повний диференціал від
в
функції
і
має
вигляд:
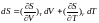(2.1)
Підставивши (2.1) в (*) знаходимо, що:
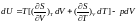(2.2)
З
рівняння Максвелла (формула
(**))
.
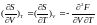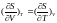Підставивши (**) в (2.2) і розкривши скобки, знаходимо:
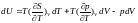(2.3)
Але
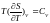і підставивши в (2.3) з виносом
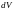за дужки маємо
(***)
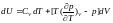Рівняння (***) є загальним рівнянням, яке показує, як змінюється внутрішня енергія системи при зміні об’єму і температури.
Внутрішня енергія газу складається з кінетичної енергії молекул, кінетичної енергії структурних елементів молекул, потенціальної енергії атомів, енергії зв’язку електронів в атомах.
.
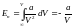Потенційна енергія – це робота, яку необхідно затратити, щоб розвести структурні елементи з точки в нескінченність.
3. Ефект Джоуля –Томсона
Фізична сутність ефекту. При розширенні газ виконує роботу. Якщо газ ізольований, тоді джерело роботи являється внутрішня енергія. Якщо б вся внутрішня енергія зводилась до кінетичної енергії частинок, тоді температура газу повинна зменшитися. Якщо б це розширення проводилося без виконання роботи, тоді температура газу не змінювалася. Процес розширення без теплообміну може бути виконаним наступним
шляхом.
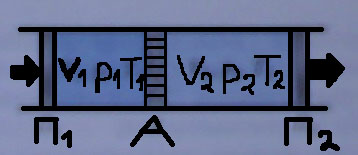
Мал. 2
Хай
є циліндр (мал.2) розділений пористою
перегородкою А. з різних сторін перегородки
один і той же газ займає об’єми
і
і знаходиться під різним тиском. Якщо
,
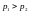тоді газ повільно проходить через
пористу перегородку з об’єму
в об’єм
.
Для підтримки тиску
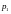і
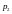постійними необхідно поршень
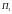здвигати в циліндр, зменшуючи при цьому
об’єм
і виконувати роботу над газом, а поршень
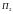– висовувати з циліндра, завдяки чому
газ виконує роботу. У випадку ідеального
газу робота, виконувана над газом у
результаті руху поршня
,
рівна роботі, виконувана газам у
результаті руху поршня
по закону Бойля –Маріотта:
.
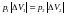
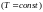По-іншому в реальному газі, коли внутрішня енергія включає в себе також потенціальну енергію взаємодії молекул. Фактично молекули знаходяться у швидкому русі і можна говорити о деякій середній відстані між ними і о середній потенціальній енергії. Середня відстань залежить від густини: чим більша густина, тим менька середня відстань. Воно також залежить від температури: чим більша температура, тим менше середня відстань. Це обумовлено тим, що при збільшенні температури кінетична енергія молекул зростає і вони при зіткненні підходять одна к одній на маленьку відстань, отже відносно велику долю часу проводять на малій відстані одна біля одної. При цих умовах ясно, що
розширення реального газу без теплообміну повинно супроводжуватися зміною його температури.
Справді,
якщо густина і температура газу достатньо
великі, то середня відстань між молекулами
менше
.
Видно, що в
розглянутому випадку при невеликому
збільшенні об’єму і, при невеликому
зменшенні тиску температура газу повинна
зрости. Якщо ж густина і температура
газу такі, що середня відстань між
молекулами більша
,
то при
невеликому збільшенні об’єму і, при
невеликому зменшенні тиску температура
газу зменшується.
Така зміна температури реального газу при дуже малій адіабатичній зміні його об’єму і тиску називається диференціальним ефектом Джоуля–Томсона. При великих змінах тиску (об’єму) необхідно просумувати малі зміни температури. Цей сумарний ефект називається інтегральним ефектом Джоуля–Томсона.
Якщо
тиски
і
по різні сторони перегородки різні на
кінцеве значення, то процес Джоуля–Томсона
може бути представлений у вигляді
квазістатичних процесів Джоуля–Томсона,
в кожному з яких тиск змінюється на
нескінченно мале значення
.
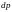Для цієї послідовності процесів
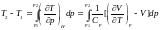(3).
Так як послідовність квазістатичних процесів Джоуля–Томсона переводить систему з такого ж початкового стану в такий же кінцевий стан, то формула (3) дає повну зміну температури в реальному процесі Джоуля–Томсона, тобто є формулою інтегрального ефекту.