3. Рівняння Пуассона

f - фи

Рівняння Пуассона дає змогу знайти потенціал у будь – якій точці поля, коли відомий розподіл густини заряду в просторі.

Диференціальна форма теорема Гаусса для напруженості поля:

_ _ _

(V * E)=divЕ=pg/ E0E

Напруженість у даній точці поля можна подати через потенціал:

_ _

E=- * f=- grad f

Підставивши цей вираз у попередню формулу, дістанемо:

_ _ _2

d iv(-gradf)=Pg/E0E або * f= f=- Pg/E0E

2

д е = - диференціальний оператор Лапласа, або ЛАПЛАСІАН.

Лапсасіан застосовується до скалярної функції координат і дає скаляр. У декартових координатах рівняння Пуассона має вигляд:

2 2 2

2 d f df df Pg

f= f =--- + --- + --- =- ----

2 2 2 E0E

dx dy dz

Насамкінець наведемо перелік використаних нами диференціальних операторів:

ГРАДІЄНТ – застосовується до скалярної функції координат, дає вектор у даній точці поля:

_dU _ dU _ dU

g rad U= U= i --- + j --- + k---

dx dy dz

1. 1. Критичний стан. Закон відповідних станів.

Найбільш повні якісні результати з рівняння Ван-дер-Ваальса можна дістати шляхом аналізу його ізотерм, побудованих за формулою (1). Помноживши рівняння (1) на і після розкриття дужок для довільних температур дістанемо

(1.1)

Рівняння (1.1) кубічне відносно молярного об’єму . Це означає, що при заданих і об’єм може набувати трьох різних значень. Коефіцієнти при у рівнянні (1.1) дійсні, і, отже, це рівняння у розв’язку може мати або всі три корені дійсні і різні, або один дійсний, а два уявні. В окремому випадку може статися, що всі дійсні корені виявляються рівними між собою. Це особливий стан речовини. Зобразимо ізотерми газу Ван-дер-Ваальсу на діаграмі стану речовини в координатах , (мал.1).

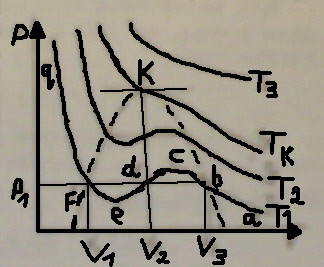
Мал. 1

Характерним на малюнку є те, що при досить високих температурах (для всіх ізотерм вище точки К) довільна ізобара перетинає ізотерму в одній точці, і цій точці відповідає одне значення об’єму, що є дійсним коренем розв’язку рівняння (1.1). Усі ізотерми в цій частині діаграми мають вигляд монотонно спадаючих з ростом об’єму гіпербол (наприклад, ). Для ізотерм нижчих, ніж у точці К, температурах довільній ізобарі відповідає три значення об’єму , , (наприклад, для ізотерми ). Ізобара перетинає ізотерму в трьох точках b, d, f, і на цій ділянці ізотерма має хвилясту форму. Для одного моля речовини її стан у точці b такий, що відповідає найбільшому об’єму з трьох зазначених, тобто . Відповідно при цьому об’ємі речовина має найменшу густину. Тому природно прийняти, що це газоподібний стан речовини. Стан речовини у точці f відповідає найменшому її об’єму , і фактично при дальшому стисненні об’єм зовсім мало змінюється, а тиск різко зростає. Це властиво рідкому стану речовини. Тому можна стверджувати, що об’єм відповідає речовині у рідкому стані.

Загальний аналіз ізотерм на мал.1 приводить, що рівняння Ван-дер-Ваальсу описує не тільки газоподібний стан реального газу, а й перехід його від газоподібного до рідкого.

З підвищенням температури (наприклад, ) горизонтальна ділянка хвилеподібної частини ізотерми звужується, мінімум і максимум хвилі зменшується. При деякій температурі ізотерма набуває точки перегину К, в якій всі три значення об’єму збігаються, що відповідає трьом дійсним і рівним між собою кореням рівняння (1.1). Температура , відповідна їй ізотерма, точка К називаються критичними. При значеннях , , кажуть, що речовина знаходиться у критичному стані.

Для визначення критичних параметрів , , виходить, що для критичної точки рівняння (1.1) можна записати так:

(1.2).

Оскільки для критичної точки всі три корені для збігаються і дорівнюють , то рівняння (1.2) є точним кубом і, отже, має зводитись до вигляду . Піднісши до кубу, дістанемо:

(1.3)

Прирівнявши коефіцієнти при однакових степенях об’єму в рівняннях (1.2) і (1.3), матимемо:

, , (1.4)

Розв’язок (1.4) дає можливість визначити , , через константи a і b:

, , (1.5).

Рівняння Ван-дер-Ваальса можна представити у такому вигляді, коли його ізотерми не залежатимуть від індивідуальних властивостей речовини. Для цього за одиниці тиску, об’єму і температури беруть критичні значення цих величин. Тоді тиск, об’єм і температуру, виміряні в цих одиницях, називають зведеними. Їх можна записати так:

, , (1.6)

Підставивши в рівняння (1) замість , , відповідно , , з (1.6) і , , з (1.5) матимемо зведене рівняння стану газу Ван-дер-Ваальса

Це рівняння є однаковим для всіх речовин, оскільки воно не містить сталих величин, які б характеризували індивідуальні властивості речовини. Це положення називається законом відповідних станів. З цього закону випливає, що коли для різних речовин із трьох параметрів , , збігаються значення яких-небудь двох, то обов’язково збігатиметься і значення третього параметра. Речовини, які підпорядковуються закону відповідних станів, називають термодинамічно подібними.