Урок 97, 98	23.01.
Числовые последовательности, способы их задания.

1. Разбор к/р.

2. Новый материал. Мы начинаем заниматься последовательностями и их пределами. Сначала – повторение. Вспомните определения конечной и бесконечной последовательностей. Приведите примеры. [1) Функция, областью определения которой является множество N всех натуральных чисел, называется бесконечной последовательностью. 2) Функция, областью определения которой является {1; 2; ... n}, то есть, первых n натуральных чисел, называется конечной последовательностью].

Замечание. Конечное количество членов последовательности может «отсутствовать», например у последовательности нет первого и десятого членов.

Вспомните определение числовой последовательности. [Последовательность называется числовой, если ее область значений является подмножеством R]

В 10 классе нас будут интересовать только бесконечные числовые последовательности. Вспомните основные способы их задания и приведите примеры [Описанием, формулой n – го члена, рекуррентно] Как можно изображать последовательности? [На координатной прямой и на координатной плоскости]

3. Письменно (самостоятельно в тетрадях с проверкой на доске):

1) Найдите первые шесть членов последовательности и изобразите их на координатной прямой [ ; ; ; 3; ; ]

2) Найдите первые шесть членов последовательности (x_n) и изобразите их на координатной плоскости, если ; .

[1; – 1; ; –0,5; 1; –1 – ]

3) Подберите формулу n – го члена последовательности: а) ; ; ; ; ... ; б) 1; ; ; ; ; ; [а) ; б) ]

4) (a_n): a₁ = 2; . Подберите формулу n – го члена и докажите.

[a_n = n(n + 1); два способа: индукция или проверка рекуррентной формулы в общем виде]

5) (b_n): b₁ = 1; b₂ = 5; b_{n + 2} = 5 b_{n + 1} – 6b_n. Докажите, что "nÎN b_n = 3ⁿ – 2ⁿ.

[Индукция с «двойным» шагом]

6) В.: стр. 96, №197 [Индукция с «двойным» шагом: от рекуррентной формулы к формуле n – го члена!]

Домашнее задание: В.: п. 3 (стр. 46 – 48); №81; №83; п. 6 (стр. 94 – 95); №193; №196.

1) При каких натуральных m и n сумму 5^m + 5ⁿ можно представить в виде суммы квадратов двух натуральных чисел?

Урок 99	27.01.
Метод математической индукции (повторение).

1. Проверка д/з: вопросы? №193 [1) ; 2) ; 3) ; 4) ; 5) ; 6) (–1)^{n + 1}×n; 7) ; 8) ] 1) [При n и k, имеющих одинаковую четность. Действительно, если числа n и k четные, то слагаемые 5ⁿ и 5^k являются полными квадратами. Если n и k нечетные, то числа 5ⁿ и 5^k можно записать в виде 5x² и 5y² для некоторых натуральных x и y, являющихся степенями пятерки. Тогда S = 5x² + 5y² = (2x + y)² + |2y – x|², где числа, возводимые в квадрат, – натуральные. Действительно, 2y x, поскольку x и y – степени пятерки.

Пусть теперь одно из чисел n или k – четное, а другое – нечетное. Пятерка в четной степени при делении на 8 дает остаток 1, а в нечетной степени – остаток 5. Поэтому число S при делении на 8 дает остаток 6. С другой стороны, квадраты натуральных чисел при делении на 8 могут давать остатки 0, 1 или 4. Поэтому сумма двух квадратов может при делении на 8 давать остатки 0, 1, 2, 4 или 5. Полученное противоречие показывает, что в данном случае число S не представимо в виде суммы двух квадратов]

Еще несколько заданий на повторение метода математической индукции.

2. Письменно (самостоятельно в тетрадях с проверкой на доске):

1) Докажите, что "nÎN 10ⁿ – 9n – 1 M 81 [... 10^k = 9k + 1 + 81m, где mÎN...]

2) Докажите, что "nÎN [... , так как ... (рассмотрим частное)]

Доказанное утверждение имеет интересное следствие: . Это числовое неравенство очень трудно доказать иным способом!

3) Вычислите (по вариантам): | [... = = 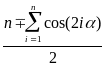(тригонометрический способ вычисления суммы косинусов, который строго доказывается только по индукции)]

Домашнее задание: В.: стр. 48, №85 (1); стр. 96, №198. Докажите, что: 1) "nÎN 6²ⁿ + 19ⁿ – 2^{n + 1} M 17; 2) "n ³ 7 2^{n – 1} > n(n + 1); 3) "nÎN ; 4) (по вариантам) "nÎN | .

Урок 100, 101	28.01.
Монотонность и ограниченность последовательностей.

1. Проверка д/з: вопросы? №85 (1) [Для доказательства A(n) = B(n) достаточно доказать, что A(1) = B(1) и A(k + 1) – A(k) = B(k + 1) – B(k)]

2. Новый материал. Вспомним понятие монотонности последовательностей. Какие последовательности считаются строго монотонными? [Возрастающие, убывающие или постоянные] Сформулируйте соответствующие определения и приведите примеры (записать на доске в краткой форме) [1) (а_n) – возрастающая Û "nÎN а_{n + 1} > а_n. Пример. а_n = n². 2) (b_n) – убывающая Û "nÎN b_{n + 1} < b_n. Пример. b_n = . 3) (с_n) – постоянная Û "nÎN c_{n + 1} = c_n. Пример. c_n = 5]. Какие последовательности считаются не строго монотонными? [Неубывающие и невозрастающие] Определения и примеры? [Знаки нестрогих неравенств; соответственно: 1; 2; 2; 3; 3; 3; ... и –1; –2; –2; –3; –3; –3; ...] Приведите пример не монотонной последовательности [x_n = (–1)ⁿ].

3. Письменно (самостоятельно в тетрадях с проверкой на доске; записи!):

1) Исследуйте на монотонность: а) а_n = ; б) с_n = n³ – 16n. [а) "nÎN а_{n + 1} – а_n = Þ а_{n + 1} > а_n Þ (а_n) – возрастает; б) с₁ = –15; с₂ = –24; с₃ = –21, то есть, с₂ < с₃ < с₁, следовательно, (с_n) – не монотонна]

2) Докажите по определению, что: а) – убывает; б) – возрастает.

[а) "nÎN и Þ b_{n + 1} < b_n Þ (b_n) – убывает; б) "nÎN x_{n + 1} > x_n Þ (x_n) – возрастает]

3) Постройте график и исследуйте на монотонность: .

[Не монотонна]

4) В.: стр. 49, №87 ["nÎN а_{n + 1} – а_n = ; докажем, что . При n = 1 а₁ = 10 > 0 и а₁² = 100 ³ 2. При n = k ; при n = k + 1: а_{k + 1} = > 0 и Û Û . Следовательно, "nÎN а_{n + 1} £ а_n, то есть, (а_n) – невозрастающая!]

4. Новый материал. Рассмотрим понятие ограниченности последовательностей.

Определение. (а_n) называется ограниченной, если $M > 0 | "nÎN |а_n| £ M.

Примеры. 1) а_n = ; M = 1 (показать на координатной прямой); 2) b_n = ; M = 2 (показать на координатной плоскости).

Эти рисунки нам еще потребуется на следующем уроке!

Обратите внимание, что если М – существует, то их – бесконечно много!

Определения. 1) (а_n) называется ограниченной сверху, если $M₁ | "nÎN а_n £ M₁.

2) (а_n) называется ограниченной снизу, если $M₂ | "nÎN а_n ³ M₂.

Примеры. 1) a_n = –2n + 2 ограничена сверху (M₁ = 0), но не ограничена снизу. 2) b_n = n² ограничена снизу (M₂ = 1), но не ограничена сверху.

Докажите, что последовательность ограничена т. и т. т., когда она ограничена сверху и снизу. [1) |а_n| £ M Û –M £ а_n £ M Þ $M₁ = M | а_n £ M₁ и $M₂ = –M | а_n ³ M₂; 2) Если $M₁ и $M₂, то M = max(|M₁|; |M₂|) (показать на координатной прямой)]

Приведите пример неограниченной последовательности. Сформулируйте ее определение [а_n = (–1)ⁿ×n²; (а_n) – не ограничена Û "M > 0 $nÎN | |а_n| > M]

5. Письменно (самостоятельно в тетрадях с проверкой на доске; записи!):

1) Докажите, что а_n = ограничена числом 4.

[Отдельно рассмотреть неравенство при n = 1 и "n ³ 2].

2) Докажите, что b_n = ограничена. [Разобрать два способа: подобрать М или доказать его существование: (b_n) – ограничена Û $M > 0 | "nÎN |b_n| £ M, то есть, "n ³ 2 Û Þ , если M > 1. Для того, чтобы это неравенство выполнялось "n ³ 2 достаточно взять M = 2]

3) Является ли c_n = ограниченной? [Да, так как "nÎN (индукция)]

4) Докажите по определению, что не ограничена [Два способа: от противного или по определению неограниченности; n = [M² + 1]]

Следующий урок – с/р!

Домашнее задание: монотонность и ограниченность – по тетради; В.: №88; №86 (на два урока). 1) Исследуйте на монотонность и ограниченность: а) ; б) ; в) . 2) Докажите по определению, что не ограничена.

Урок 102, 103	30.01.
Самостоятельная работа №9. Определение предела последовательности.

1. Проверка д/з: вопросы? №88 ["nÎN а_{n + 1} – а_n = ; так как а_n ³ 0, то Û Û 0 £ а_n £ 2 (индукция)] 1) а) возрастающая, ограниченная (М = 1); б) убывающая, ограниченная (М = 1); в) не монотонная, ограниченная (М = 1). 2) n! > n > M выполняется при n = [M] + 1.

2. Самостоятельная работа №9 (на листочках; 35 минут).