5.1.2 Максимальное, действующее и среднее значение несинусоидальной величины

Периодически изменяющуюся несинусоидальную величину , помимо ее гармонических составляющих, характеризуют следующие величины:

1. максимальное значение ;

2. среднее квадратичное за период или действующее значение

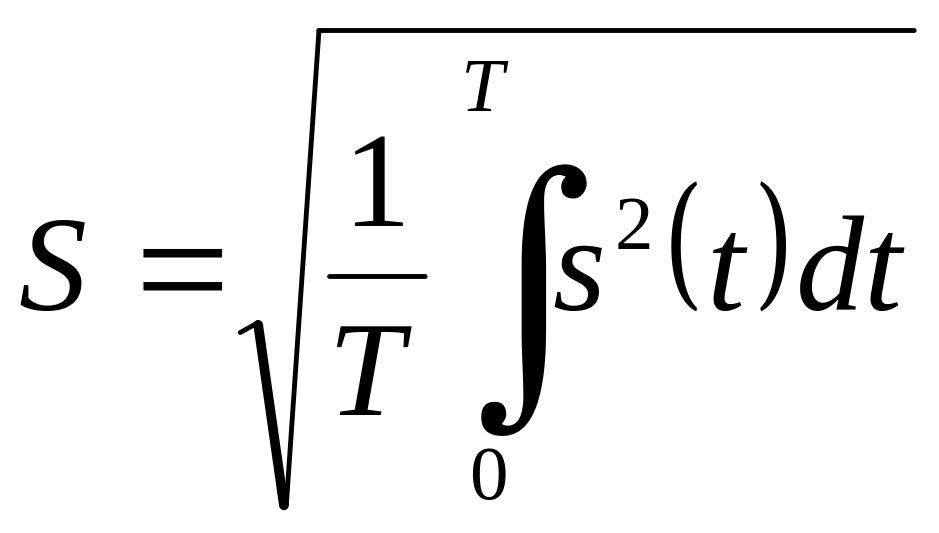; (5.6)

3. среднее по модулю значение

. (5.7)

Если кривая симметрична относительно оси абсцисс и в течение половины периода функция ни разу не изменяет знака, то среднее по модулю значение равно среднему значению за половину периода:

, (5.8)

причем в формуле (5.8) начало отсчета времени должно быть выбрано так, чтобы . В тех случаях, когда за весь период функция ни разу не изменяет знака (см., например, рисунок 5.3, б), среднее по модулю значение равно постоянной составляющей .

Если периодическая несинусоидальная функция задана аналитическим выражением, то действующее и среднее значения определяются непосредственно на основании интегральных соотношений (5.6) – (5.8). Если же периодическая несинусоидальная функция представлена в виде разложения в тригонометрический ряд, то действующее значение может быть найдено по формуле

, (5.9)

(5.9)

где , ,   ,     — действующие значения гармоник, представляющих ряд (5.1).

5.1.3 Коэффициенты, характеризующие форму несинусоидальных кривых

При оценке формы периодических несинусоидальных величин используют следующие характеристики: коэффициент формы , коэффициент амплитуды и др.

Коэффициент формы определяется как отношение действующего значения к среднему по модулю значению:

. (5.10)

Коэффициент амплитуды равен отношению максимального значения величины к ее действующему значению:

. (5.11)

Для синусоидальных величин вышеуказанные характеристики равны: , .

5.1.4 Расчет электрической цепи с постоянными параметрами при действии несинусоидальной эдс

Расчет цепи начинается с разложения несинусоидального напряжения источника в ряд Фурье (5.1):

, (5.12)

где — постоянная составляющая напряжения, — амплитуда гармоники с номером , — начальная фаза этой гармоники.

Так как для линейных цепей применим принцип наложения, то ток в этой цепи будет равен сумме токов, получаемых от действия каждой из составляющих ряда (5.12):

. (5.13)

Здесь — это постоянная составляющая силы тока, — амплитуда - й гармоники, — ее начальная фаза.

Значения , и для каждой из составляющих ряда (5.13) в общем случае можно рассчитать символическим методом. Для схем цепей, изображенных на рисунке 5.2, указанный расчет может быть выполнен и более простым способом:

,      ,      ,      , (5.14)

где — полное сопротивление цепи при нулевой частоте , т.е. сопротивление постоянному току, и — полное и реактивное сопротивления при частоте , — активное сопротивление.

а)	б)	в)
Рисунок 5.2 – Простейшие схемы последовательных цепей, содержащих резистор, индуктивную катушку и конденсатор

В случае цепи с последовательным соединением элементов ,   и  (рисунок 5.2, а) указанные величины равны:

,      ,      . (5.15)

Для ,   – цепи (рисунок 5.2, б)

,      ,      , (5.16)

для ,   – цепи (рисунок 5.2, в)

,      ,      . (5.17)