5.4 Дифференцирование параметрически заданных
и неявных функций
а) Функции, заданные параметрически.
Пусть
дана функция
,
причём
непрерывна и строго возрастает. Тогда
определена обратная функция
и
.
По тереме о дифференцировании сложной
функции и теореме о дифференцировании
обратной функции,
.
Итак,
.
б) Функции, заданные неявно.
Если
дифференцируемая функция
задана неявно уравнением
,
то нужно продифференцировать это
равенство по x,
учитывая, что
есть функция от x,
а затем выразить оттуда
.
Пример
Найти
для функции, заданной неявно уравнением
.
Решение. Продифференцируем обе части данного равенства по x, учитывая, что есть функция от x, получим:
.
Итак,
.
5.5 Производные и дифференциалы высших порядков
Пусть
имеет производную во всех точках
интервала
.
Если функция
имеет производную в точке
,
то её называют второй производной или
производной II
порядка функции
.
Обозначается
или
.
И т.д.
.
Физический
смысл
.
Пусть материальная отточка движется
по закону
.
Тогда скорость
.
Отношение
–
это ускорение точки на промежутке
времени
.
Предел этого ускорения равен
– это ускорение в момент
.
Если
функция задана параметрически:
,
то
.
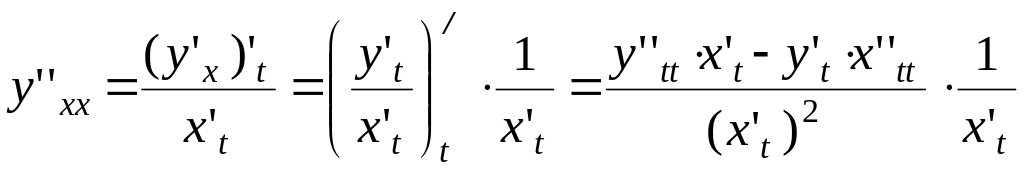Итак,
.
Аналогично получается
.
Пример
Найти
и
,
если
,
.
Решение.
.
Тогда
.
.
Рассмотрим пример неявно заданной функции.
Пример
Найти
и
, если
.
Решение. Продифференцируем обе части данного равенства по x, учитывая, что есть функция от x, получим:
.
Выразив
отсюда
,
получим
.
Продифференцируем обе части последнего равенства по x, учитывая, что есть функция от x, получим:
.
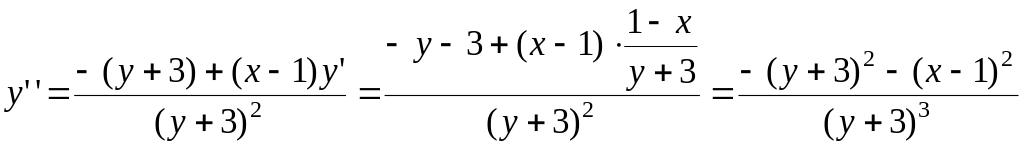Теорема
(формула
Лейбница)
Если U
и V
имеют в точке x
производные n-го
порядка, то
тоже имеет производную n-го
порядка, причём
,
где
,
.
То есть
.
Дифференциалы высших порядков:
.
6 Основные теоремы для дифференцируемых функций
6.1 Точки локального экстремума
О.
Функция
имеет в точке
локальный
максимум,
если существует такая окрестность
точки
,
что
.
О.
– точка
строгого локального максимума,
если
.
О. Функция имеет в точке локальный минимум, если существует такая окрестность точки , что
.
О. – точка строгого локального максимума, если
.
Локальный максимум и локальный минимум объединяются названием локальный экстремум.
6.2 Теорема Ферма
Теорема
Ферма
Если
имеет в точке
локальный экстремум и дифференцируема
в этой точке, то
.
Доказательство.
Пусть
имеет в точке
локальный минимум. Это значит, что в
некоторой окрестности точки
.
Тогда
если
,
то
,
если
,
то
.
Перейдем к пределу при
.
Получим
.
Так
как
дифференцируема в точке
,
то
.
Из последних неравенств следует, что
,
и в то же время
.
Значит,
.
■
Геометрический смысл теоремы Ферма: касательная к графику функции в точке локального экстремума параллельна оси Ох.