
- •1 Действительные числа
- •1.1 Логическая символика и терминология
- •1.2 Аксиоматика действительных чисел
- •1.3 Точные грани числовых множеств
- •1.4 Натуральные, рациональные, иррациональные числа
- •1.5 Принцип Кантора
- •1.6 Правило построения отрицания
- •2 Числовые последовательности
- •2.1 Определения
- •2.2 Предел последовательности
- •2.3 Общие свойства предела последовательности
- •2.4 Свойства сходящихся последовательностей, связанные с неравенствами
- •2.5 Бесконечно малые последовательности
- •2.6 Бесконечно большие последовательности
- •2.7 Арифметические операции над сходящимися последовательностями
- •2.8 Предел монотонной последовательности
- •2.9 Число e
- •2.10 Подпоследовательности. Частичные пределы
- •2.11 Критерий Коши сходимости последовательности
- •3 Предел функции в точке
- •3.1 Определение предела по Коши
- •3.2 Определение предела по Гейне
- •3.3 Различные типы пределов
- •3.4 Свойства пределов функции в точке
- •3.5 Предел монотонной функции
- •3.6 Бесконечно малые функции
- •3.7 Замена переменной при вычислении предела (или предел композиции функций)
- •3.8 Первый замечательный предел
- •3.9 Второй замечательный предел
- •3.10 Сравнение асимптотического поведения функций
- •4 Непрерывные функции
- •4.1 Определение
- •4.2 Точки разрыва
- •4.3 Свойства функций, непрерывных в точке (локальные свойства непрерывных функций)
- •4.4 Свойства функций, непрерывных на отрезке (глобальные свойства непрерывных функций)
- •5 Производная функции в точке
- •5 .1 Определение. Физический и геометрический смысл производной
- •5.2 Дифференциал функции
- •5.3 Правила дифференцирования
- •5.4 Дифференцирование параметрически заданных
- •5.5 Производные и дифференциалы высших порядков
- •6 Основные теоремы для дифференцируемых функций
- •6.1 Точки локального экстремума
- •6.2 Теорема Ферма
- •6.3 Теорема Ролля
- •7 Формула Тейлора
- •Формулы Маклорена для некоторых элементарных функций
- •8 Правило Лопиталя
- •9 Исследование функций с помощью производной
- •9.1 Возрастание и убывание функций
- •9.2 Экстремумы функции
- •9.3 Наибольшее и наименьшее значения функции на отрезке
- •9.4 Выпуклость функции
- •9.5 Точки перегиба
- •9.6 Асимптоты
- •9.7 Схема исследования функции
5 Производная функции в точке
5 .1 Определение. Физический и геометрический смысл производной
Пусть
![]() – путь, пройденный материальной точкой
за время t.
Тогда средняя скорость материальной
точки за промежуток
– путь, пройденный материальной точкой
за время t.
Тогда средняя скорость материальной
точки за промежуток
![]() есть величина, равная
есть величина, равная
![]() .
.
Тогда
![]() мгновенная скорость движения материальной
точки в момент времени
мгновенная скорость движения материальной
точки в момент времени
![]() .
.
Обозначим
![]() –
приращение аргумента х,
–
приращение аргумента х,
![]() –
приращение
функции
,
соответ-ствующее приращению
.
–
приращение
функции
,
соответ-ствующее приращению
.
О.
Производной
функции в точке
называется число (если оно существует),
равное пределу отношения приращения
функции в точке
к приращению аргумента при условии, что
![]() и обозначается
и обозначается
![]() ,
т. е.
,
т. е.
![]() .
.
Механический
смысл производной.
Если х
– время,
![]() – путь, пройденный материальной точкой
за время х,
то
– это скорость движения в момент времени
или
–мгновенная скорость изменения функции
в момент времени
.
– путь, пройденный материальной точкой
за время х,
то
– это скорость движения в момент времени
или
–мгновенная скорость изменения функции
в момент времени
.
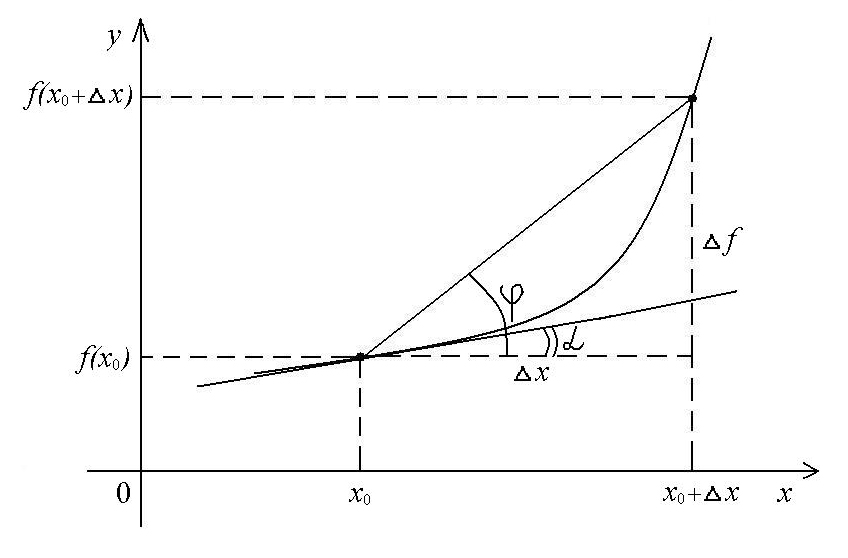
Геометрический
смысл производной.
![]() –
это тангенс угла наклона секущей,
проходящей через точки с координатами
–
это тангенс угла наклона секущей,
проходящей через точки с координатами
![]() и
и
![]() .
.
При
![]()
![]() –
тангенс угла наклона касательной,
проведенной к графику функции
в точке
.
–
тангенс угла наклона касательной,
проведенной к графику функции
в точке
.
Если
![]() уравнение
касательной, то
уравнение
касательной, то
![]() .
.
Уравнение
касательной:
![]() .
.
Примеры
1)
![]() .
.
![]() ,
т. е. производная постоянной функции
равна 0.
,
т. е. производная постоянной функции
равна 0.
2)
![]() .
Покажем, что
.
Покажем, что
![]() .
Действительно,
.
Действительно,
![]()
![]() .
.
3)
![]() .
.
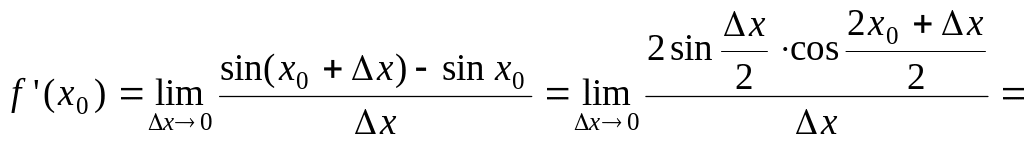
![]() т.
е.
т.
е.
![]() .
.
Теорема Если имеет производную в точке , то непрерывна в точке .
Доказательство.
Из равенства
![]() следует, что
следует, что
![]() при
.
Отсюда
при
.
Отсюда
![]() при
.
при
.
Значит,
![]() при
.■
при
.■
Замечание. Если разрывна в точке , то она не имеет производной в точке .
По аналогии с односторонними пределами вводятся понятия односторонних производных:
![]() ,
,
![]() – правосторонняя и левосторонняя
производные функции
в точке
.
– правосторонняя и левосторонняя
производные функции
в точке
.
Пример
![]() .
Найти односторонние производные.
.
Найти односторонние производные.
Решение.
![]() ,
,
![]() .
.
Так
как односторонние производные не равны,
то
![]() не имеет производной в точке
не имеет производной в точке
![]() .
.
5.2 Дифференциал функции
Пусть функции определена в некоторой окрестности точки .
О. Функция называется дифференцируемой в точке , если её приращение в точке представимо в виде:
![]() ,
,
где
А
– постоянная, не зависящая от
(но зависящая от
),
а функция
![]() при
.
при
.
Слагаемое
![]() называется дифференциалом
функции
в точке
и обозначается
называется дифференциалом
функции
в точке
и обозначается
![]() или
или
![]() .
Дифференциал – это главное линейная
часть приращения функции. Тогда
.
Дифференциал – это главное линейная
часть приращения функции. Тогда
![]() ,
.
,
.
Теорема Функция дифференцируема в точке тогда, и только тогда, когда она имеет производную в точке . При этом
![]() .
.
Доказательство.
Необходимость. Если дифференцируема в точке , то приращение функции в точке представимо в виде:
.
Отсюда
![]() ,
где
при
.
,
где
при
.
Следовательно,
при
существует
![]() и
и
![]() .
.
Достаточность. Если , то .
Следовательно,
![]() .■
.■
Обычно
обозначают
![]() и пишут
и пишут
![]() .
.
Механический
смысл дифференциала:
![]() ,
т.е. дифференциал равен расстоянию,
которое прошла бы материальная точка
за промежуток времени
,
т.е. дифференциал равен расстоянию,
которое прошла бы материальная точка
за промежуток времени
![]() ,
если бы она двигалась со скоростью
,
если бы она двигалась со скоростью
![]() .
.
5.3 Правила дифференцирования
Теорема 1 Если функции и дифференцируемы в точке , то в этой точке дифференцируемы функции
![]()
![]() (если
(если
![]() ),
),
причем
1)
![]() ,
,
2)
![]() ,
,
3)
![]() ,
,
![]() .
.
Доказательство.
1) Если
![]() ,
то
,
то
![]() .
.
Тогда
![]() .
При
предел правой части существует, значит,
существует и предел левой части. При
получаем
.
.
При
предел правой части существует, значит,
существует и предел левой части. При
получаем
.
2)
Пусть
![]() .
Тогда
.
Тогда
![]()
![]() .
.
Отсюда
следует, что
![]() .
.
Так
как
![]() дифференцируема в точке
,
то
дифференцируема в точке
,
то
![]() при
.
Поэтому из последнего равенства при
получаем
при
.
Поэтому из последнего равенства при
получаем
![]() .
.
3) Доказательство предлагается изучить самостоятельно.■
Следствие
![]() ,
где
,
где
![]() .
.
Пример
Доказать,
что
![]() .
.
Решение.
![]()
![]() .
.
Теорема
2
(производная обратной функции) Если
функция
непрерывна и строго возрастает (убывает)
на отрезке
![]() и если
и если
![]() ,
то функция
,
то функция
![]() ,
обратная к функции
,
дифференцируема в точке
,
обратная к функции
,
дифференцируема в точке
![]() ,
причем
,
причем
![]() .
.
Доказательство
следует из равенства
![]() .
.
Пример
Доказать, что
![]() ,
при
,
при
![]() .
.
Решение.
Здесь
![]() .
.
Тогда
обратная функция
![]() ,
,
![]() .
По формуле,
.
По формуле,
![]()
![]() .
.
Теорема
3
(дифференцирование сложной функции)
Если
![]() дифференцируема в точке
,
дифференцируема в точке
,
![]() дифференцируема в точке
,
то сложная функция
дифференцируема в точке
,
то сложная функция
![]() дифференцируема в точке
дифференцируема в точке
![]() ,
причем
,
причем
![]() .
.
Таблица производных от основных элементарных функций
1)
![]()
2)
![]() ,
,
![]() ,
,
![]() ,
,
![]()
3)
![]() ,
,
![]()
4)
![]() ,
,
![]()
5)
![]() ,
6)
,
6)
![]()
7)
![]() ,
8)
,
8)
![]()
![]()
9)
![]() ,
10)
,
10)
![]()
11)
![]() ,
12)
,
12)
![]()
13)
![]() ,
14)
,
14)
![]()
15)
![]() ,
16)
,
16)
![]()
