
- •Пояснительная записка
- •Краткие методические рекомендации для самостоятельной работы
- •Правила выполнения расчетно-графической работы.
- •Образцы выполнения работ ргр №1 Тема: «Матрицы и определители»
- •Ргр №2 Тема: «Системы линейных алгебраических уравнений»
- •Ргр №3 Темы: «Векторы» и «Уравнения прямых и плоскостей»
- •Ргр №4 Тема: «Кривые 2-го порядка и уравнения прямых и плоскостей»
- •Ргр №5 Тема: «Непрерывность функций»
- •Ргр №6 Тема: «Предел функции. Дифференцирование. Исследование функций и построение графиков».
Ргр №4 Тема: «Кривые 2-го порядка и уравнения прямых и плоскостей»
Задание 1. Составить уравнение
прямой, проходящей через левый фокус
гиперболы, ![]()
![]()
Из уравнения окружности
![]() -центр.
-центр.

Каноническое уравнение
гиперболы имеет вид: ![]()
Для приведения к нему поделим всё уравнение на правую часть и получим:
![]()
Сравнивая с общим видом канонического уравнения, получим:
![]()
![]()
Зная a и b найдём координаты вершин гиперболы и параметры основного прямоугольника (см. чертёж):
![]()
![]()
![]()
![]()
Для нахождения фокуса гиперболы воспользуемся формулой
![]()
Подставим значения a и b , и получим координаты фокусов гиперболы.
![]()
![]()
![]()
Получим две точки фокуса.
![]()
![]()
Необходимо составить
уравнение прямой, проходящей через ![]() и центр окружности
и центр окружности![]() .
Для решения воспользуемся формулой,
где (
.
Для решения воспользуемся формулой,
где (![]() )и
(
)и
(![]() )
координаты точек
)
координаты точек ![]() и S.
и S.
![]()

Преобразуем уравнение и упростим для приведения его к виду уравнения с угловым коэффициентом:
![]()
![]()
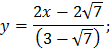

Ргр №5 Тема: «Непрерывность функций»
Задание 1.Выяснить характер точек разрыва функции или доказать её непрерывность.
а)
Н
при
точка
разрыва II
рода, т.к. есть точка бесконечного
разрыва;
![]()
![]() и слева и справа.Т.е предел стремиться
и слева и справа.Т.е предел стремиться
![]() левый предел
левый предел ![]() правый
правый ![]()
![]()
![]() ⇒
⇒
Найдём
предел при![]() слева
и справа. Т.е предел стремиться
слева
и справа. Т.е предел стремиться
![]() ;
левый
предел
;
левый
предел![]() ,
правый
,
правый
![]()
при

![]() - скачок, точка разрыва I
рода, т.к. согласно формуле
- скачок, точка разрыва I
рода, т.к. согласно формуле ![]()
![]()
![]()
б)
![]()
Найдем точки возможного разрыва, для этого приравняем знаменатель к нулю и решим квадратное уравнение:
![]()
![]()
![]()
![]()
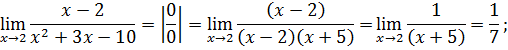
![]()
![]()
![]()
![]()
![]()
Задание 2.Построить график функции и исследовать характер точек разрыва.

Найдём
предел при ![]() слева и справа.
слева и справа.
Точка
разрыва I рода, скачок.![]()
![]()
![]()
y




-1
1
x
![]()

![]()
![]()
![]()
Задание 3. Подобрать α, чтобы функция была непрерывной.
Доказать непрерывность функции при найденном α и разрывность при каком-либо другом α.

Подставим
![]() именно для того, чтобы функция была
непрерывна, т.к. при подстановке в
выражение 0, получается 0.
именно для того, чтобы функция была
непрерывна, т.к. при подстановке в
выражение 0, получается 0.
![]()
![]()
⇒
![]()
![]()
Если
например ![]() ,
то правый предел функции уже будет не
равен 0⇒
функция разрывна;
,
то правый предел функции уже будет не
равен 0⇒
функция разрывна;
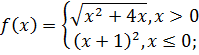
Найдём левый и правый предел.
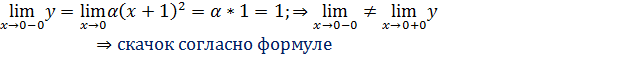
![]()
![]()
Ргр №6 Тема: «Предел функции. Дифференцирование. Исследование функций и построение графиков».
Задание 1. Вычислить пределы.
Найдём предел, поделив и
числитель, и знаменатель на высшую
степень ![]()
При подстановке в уравнение получаем неопределённость. Для того чтоб от неё избавиться помножим и разделим на сопряжённое данному выражению
 Задание
2. Вычислить
производные
Задание
2. Вычислить
производные
Найдём предел отношения приращения функции к приращению аргумента при стремлении аргумента к 0, т.е. производную, используя формулы и правила дифференцирования, изученные в течение курса.
Функция представляет собой сумму элементарных функций, а производная суммы функций равна сумме их производных, причём постоянный множитель выносится за знак производной.
![]()
Функция
представляет собой частное элементарных
функций. Воспользуемся для дифференцирования
формулой:
![]()
![]()
![]()
Функция
представляет собой произведение
элементарных функций. Воспользуемся
для дифференцирования формулой:
![]()

Задание 3. Исследовать функцию и построить график
![]()
Исследуем функцию по схеме.
Найдём
область определения функции, т.е.
определим какие значения может принимать
![]() .
.
Найдём точки пересечения графика функции с осями координат.
![]() ;
;
-
+
-
x

![]()
![]()
Выясним чётность и
нечётность функции, если ![]() - функция чётная, если
- функция чётная, если ![]() -
функция нечётная, если ни одно из этих
равенств не выполняется, то функция
общего вида.
-
функция нечётная, если ни одно из этих
равенств не выполняется, то функция
общего вида.
Найдём производную функции, из которой выясним, есть ли критические (точки, в которых производная не существует) или стационарные точки (точки, в которых производная равна 0).
![]()
![]()
![]() стационарные
точки;
стационарные
точки;
-
![]()
+
-
x
+

![]()
-

![]()
![]()


![]()
![]()
![]() точка
max.,
точка
max., ![]() точка min.
точка min.
Найдём значение функции в этих точках


Максимальное
значение ![]() , минимальное значение
, минимальное значение ![]()
Найдём вторую производную, т.е. производную от результата первой производной, из чего получим интервалы выпуклости и вогнутости и координаты точек перегиба,.
-
+
+![]()
![]()



Найдём асимптоты, т.е. прямые обладающие свойством, что расстояние от точки
 до этой прямой стремится к 0, при
неограниченном удалении точки графика
от начала координат.
до этой прямой стремится к 0, при
неограниченном удалении точки графика
от начала координат.
Вертикальную
асимптоту найдём как предел функции
стремящейся к точке разрыва в области
определения, т.е. к ![]()
![]()
Горизонтальную асимптоту найдём как предел функции при х стремящейся к бесконечности.
![]()
![]()
![]() =
=![]()
![]() наклонная
асимптота
наклонная
асимптота
7
y


 .
Построим
график
.
Построим
график
2
x
2



![]()
В заключение отметим, что при изучении математики очень существенно решение задач. Еще Ньютон высказывал мнение, что эта сторона дела важнее, чем усвоение теории. Конечно, полностью с этим согласиться нельзя, но нет сомнения, что для специалиста одно лишь теоретическое знакомство с материалом было бы бесполезно. Поэтому студенты должны сочетать изучение лекций с решением задач из задачников по высшей математике и расчетно-графических работ.
