3. Площина у просторі.

3.1. Загальне рівняння площини. Нормальний вектор.

Нехай в просторі задано точку та вектор . Складемо рівняння прямої, що проходить через точку перпендикулярно вектору . Візьмемо довільну точку площини , тоді вектор перпендикулярний вектору , тому скалярний добуток , або (3.1). Одержали рівняння площини, що проходить через точку перпендикулярно вектору . Якщо розкрити дужки та позначити , то рівняння площини набуває вигляду:

Означення 4. Загальним рівнянням площини називається рівняння , а вектор – нормальним вектором цієї площини.

3.2. Рівняння площини, що проходить через три задані точки. , ,

Нехай – довільна точка площини. Розглянемо вектори: ;

;

.

Ці вектори належать площині, тому компланарні. Як відомо, умова компланарності полягає в тому, що мішаний добуток цих векторів дорівнює нулю, тобто , або в координатній формі: (3.2)

Приклад 7

Записати рівняння площини, що проходить через три точки: , ,

Розв’язання.

Використавши рівняння (3.2), запишемо: ,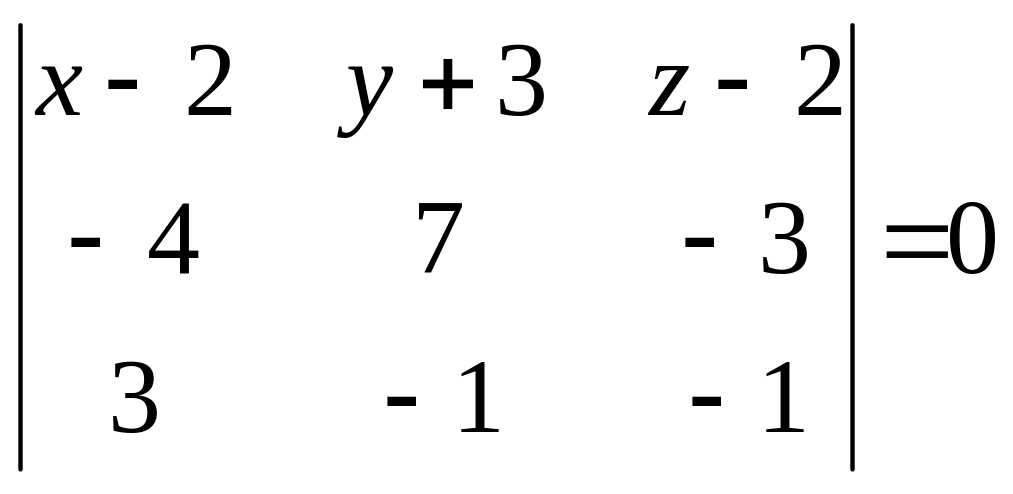

Розкривши визначник, одержуємо: , ,

Відповідь:

3.3. Нормальне рівняння площини. Нормувальний множник. Відстань від точки до площини.

Означення 5. Нормальним рівнянням площини називається рівняння , де – напрямні косинуси нормального вектора , – відстань від початку координат до площини. Загальне рівняння площини приводиться до нормального вигляду множенням на нормувальний множник де знак перед коренем вибирається протилежним знаку вільного члена D.

Теорема 4

Відстань від точки до площини P: обчислюється за формулою: (3.3)

Приклад 8

Обчислити відстань від точки М( 1; - 2 ; 4) до площини

Розв’язання.

Підставимо в формулу (3.3) координати точки М і обчислимо

Відповідь:

3.4. Кут між двома площинами. Умови паралельності та перпендикулярності площин.

Теорема 5

Якщо площини задано загальними рівняннями , , то кут між ними обчислюється за формулою:

( 3.4)

Приклад 9

Знайти косинус кута, утвореного площинами та у = 0.

Розв’язання.

Запишемо нормальні вектори площин та .

За формулою (3.4)

Відповідь:

Теорема 6

Дві площини, які задано загальними рівняннями та паралельні тоді і тільки тоді, коли .

Теорема 7

Дві площини, які задано загальними рівняннями: та , перпендикулярні тоді і тільки тоді, коли

Приклад 10

Скласти рівняння площини Р , що проходить через точку М( 2, 3, -3) паралельно площині Q:

Розв’язання

Нормальний вектор площини Q : .

Площина Р паралельна до площини Q, тому її нормальний вектор

Використавши рівняння площини, що проходить через задану точку М перпендикулярно до вектора (3.1) , одержимо , звідки Р:

Відповідь:

4. Пряма у просторі.

4.1. Канонічні рівняння прямої.

Нехай задано точку і вектор . Складемо рівняння прямої L, що проходить через точку паралельно вектору . Візьмемо довільну точку на прямій і розглянемо вектор . Вектори та – колінеарні, тому їх координати пропорційні, тобто (4.1).

Співвідношення (4.1) називаються канонічними рівняннями прямої, а вектор – напрямним вектором цієї прямої.

Приклад 11

Скласти рівняння прямої, що проходить через точки і .

Розв’язання.

Напрямним вектором прямої виберемо вектор .

Використавши рівняння (4.1), запишемо – канонічні рівняння прямої, яка проходить через точки і .

4.2. Параметричні рівняння прямої.

Якщо загальне відношення канонічних рівнянь позначити через t: , то одержимо (4.2) – параметричні рівняння прямої, де

Приклад 12

Знайти точку перетину прямої L : і площини P: 3x + 5y – z – 2 = 0.

Розв’язання.

Запишемо канонічні рівняння даної прямої: , звідки одержуємо

Підставимо ці вирази у рівняння площини P та отримаємо: 3(4t + 12) + 5( 3t + 9) – t – 2 = 0, звідки одержуємо t = -3.

Запишемо координати точки перетину прямої та площини:

Відповідь: M(0, 0, 2 )

4.3. Загальні рівняння прямої.

Пряму у просторі можна задавати перетином двох не паралельних площин: (4.3) – це загальні рівняння прямої, визначеної перетином двох площин.

Приклад 13

Записати канонічні рівняння прямої, яку задано загальними рівняннями:

Розв’язання.

Знайдемо координати будь-якої точки, що належить прямій. Нехай х=0, тоді одержимо систему: , звідки знаходимо: . Шукана точка

За напрямний вектор візьмемо – векторний добуток нормальних векторів площин, лінією перетину яких задана пряма. Таким чином,

Запишемо канонічні рівняння прямої, використавши (4.1):

Відповідь:

4.4. Умови паралельності та перпендикулярності прямих.

Теорема 8

Якщо дві прямі задано канонічними рівняннями і , то кут між ними обчислюється за формулою:

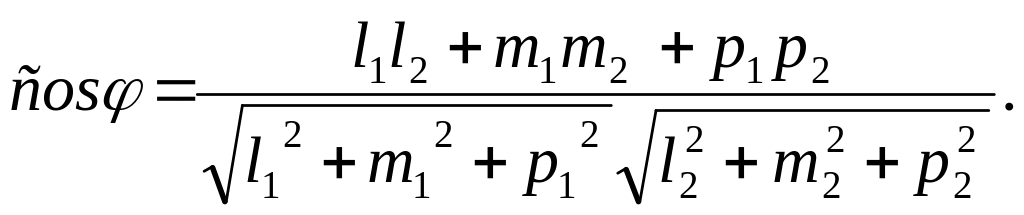
Умова паралельності: ;

Умова перпендикулярності:

Приклад 14

Задано рівняння прямої : і точка М( 2, 3, -3). Знайти рівняння , що проходить через точку М паралельно прямій .

Розв’язання.

З напрямний вектор прямої візьмемо напрямний вектор прямої : .

Використавши канонічні рівняння (4.1), запишемо рівняння прямої :

Відповідь:

4. 5. Умови паралельності та перпендикулярності прямої і площини.

Нехай пряму L та площинy P задано рівняннями: L: ; P: . Тоді напрямний вектор прямої та нормальний вектор площини .

Теорема 9

Пряма L паралельна до площини P тоді і тільки тоді, коли .

Теорема 10

Пряма L перпендикулярна до площини P тоді і тільки тоді, коли вектори та – колінеарні, тобто

Приклад 15

Знайти рівняння площини P: 3x + 5y – z – 2 = 0, яка проходить через точку M(-2, 5, 1) перпендикулярно до прямої L:

Розв’язання.

Нормальним вектором площини виберемо напрямний вектор прямої .

Використовуючи рівняння площини , складаємо рівняння шуканої площини . Перетворивши це рівняння, одержуємо

Відповідь: