3.3. Непрерывные n–мерные случайные величины
Если функция
абсолютно непрерывна, то случайная
величина
называется непрерывной. Совместную
функцию распределения в этом случае
можно записать в виде n-кратного
интеграла
и функция
– плотность распределения n–мерной
случайной величины
.
Как и в случае одномерной сл. величины
будем полагать выполнение почти всюду
равенства
(3.8)
Свойства совместной плотности распределения
1.
.
2.
.
3.
Если
,
то
.
4.
Условие согласованности для совместной
плотности распределения имеет вид
и
–
маргинальная совместная плотность
распределения случайной величины
.
В частности,
,
– маргинальные плотности распределения
сл. величин
,
.
При n=2 свойства совместной функции распределения принимают вид:
1.
;
2.
;
3.
;
4.
;
.
В заключение рассмотрим наиболее часто встречающееся на практике многомерное нормальное распределение (гауссово распределение).
Говорят, что сл. вектор , компонентами которого являются непрерывные сл. величины , , распределен по нормальному закону, если совместная плотность распределения вектора определяется формулой:
(3.9)
где
,
–
вектор математического ожидания сл.
величины
или вектор средних, положительно
определенная симметричная матрица A
носит название ковариационной матрицы,
–
определитель этой матрицы. Вектор m и
матрица A – параметры многомерного
нормального распределения.
Если m=0
и A=I,
то
–
совместная плотность стандартного
нормального распределения.
Пусть n=2,
.
Вектор m
и матрица A могут быть параметрами
двумерного нормального распределения,
так как A > 0, симметрична. Определитель
матрицы A равен 1,
,
квадратичная форма
имеет вид
.
Тогда плотность распределения двумерной
сл. величины выглядит следующим образом:
3.4. Условные распределения
Для простоты
изложения ограничимся случаем n
= 2. Итак, пусть
– двумерная случайная величина с
известными функциями
и
.
Известно, что сл. величина
приняла значение
.
Что можно сказать о распределении сл.
величины
при условии
?
Из самой постановки вопроса видно, что
понятие условного распределения весьма
схоже с определением условной вероятности
событий, рассмотренной в п. 1.8.
Начнем с наиболее
простого случая, пусть
– дискретная величина. Назовем условной
функцией распределения
случайной величины
при условии
условную вероятность события {
}
при условии события
,
то есть
.
(3.10)
Условная функция
распределения обладает всеми свойствами
функции распределения.
Если
также дискретная случайная величина,
причем
,
то удобно вместо условной функции
распределения рассматривать условные
вероятности
случайной величины
,
которая принимает значение xi
при условии
,
определяемые как
(3.11)
Составим таблицу:
Таблица 4
ξ\η |
y1 |
y2 |
… |
ym |
|
x1 |
|
|
… |
|
|
x2 |
|
|
… |
|
|
… |
… |
… |
… |
… |
… |
xn |
|
|
… |
|
|
|
|
|
… |
|
|
Ясно, что эта
таблица получается из табл. 3 из п.3.2
заменой в ней элементов рij
элементами
,
вычисляемыми по формуле (3.11):
.
Так, например,
и
т.д. Очевидно, таблицу 3 можно получить
из таблицы 4 заменой элементов
на рij
по формуле
(3.12)
Пусть теперь
не является дискретной величиной.
Формулой (3.10) для определения условной
функции распределения пользоваться в
этом случае не можем, так как
.
Перейдем от события
к событию
,
а событие
получим из события
при
.
Определим
и назовем условной функцией распределения
предел этой условной вероятности при
:
(3.13)
Поскольку событие
есть объединение непересекающихся
событий
и
,
кроме того, событие
,
то согласно следствию из свойства Р3
вероятностей имеем
Итак,
(3.14)
Так как
,
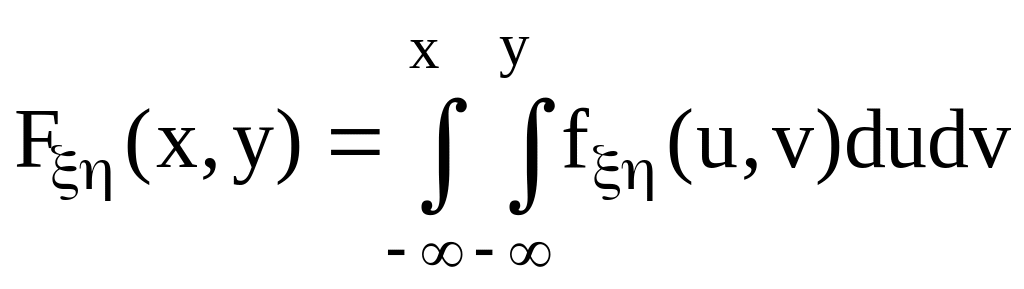то второй сомножитель в формуле (3.14)
можно переписать в виде
,
следовательно,
(3.15)
Если функция имеет производную по x , т.е. существует условная плотность распределения случайной величины при условии
(3.16)
С использованием
свойства 4 совместных плотностей
распределения и опустив в левой части
у функции
индекс
получим:
(3.17)
Аналогичным рассуждением может быть получена формула:
(3.18)
Из формул (3.16) и (3.18) можно получить соотношения:
,
(3.19)
которые напоминают формулы умножения вероятностей для случайных событий.
Пример 2. Пусть
(ξ,η) – нормально распределенный случайный
вектор с ковариационной матрицей
,
вектором средних
(см.
равенство (3.9)). Найдем условное
распределение случайной величины
при условии η=y.
Решение. Сначала
вычислим матрицу
:
.
Тогда согласно
формуле (3.9):
(3.20)
.
(3.21)
Видим, что условное
распределение сл. величины
при условии
–
формула (3.21) – снова будет нормальным
со средним значением
и средним квадратическим отклонением
.
Отметим еще, что
маргинальное распределение
– формула (3.20) – также является нормальным
со средним значением m2
и средним квадратическим отклонением
.
Определение. Случайные величины называются независимыми, если имеет место равенство:
(3.22)
или же, через плотности распределения,
(3.23)
В этом случае условные плотности распределений совпадают с плотностями распределений. Так, при n=2 в случае независимости случайных величин и имеем:
и
(3.24)
Отметим, что дискретные сл. величины будут независимыми, если:
(3.25)