Дисперсия случайной величины
Математическое ожидание не всегда является достаточной характеристикой сл. величины, оно является наиболее типичным значением сл. величины в серии испытаний, а в каждом отдельном испытании значения сл. величины отклоняются от её математического ожидания в ту или иную сторону. Поэтому наряду со средним значением сл. величины хорошо бы иметь величину, характеризующую отклонение сл. величины от своего среднего. Ведь одна ситуация, если отклонение сл. величины от своего среднего в ту или иную сторону (еще говорят разброс вокруг среднего значения) составляет 1 единицу, но совсем другая – если, например, 10 единиц.
Такой характеристикой обычно служит дисперсия сл. величины.
Определение. Дисперсией случайной величины называют число:
(2.18)
Величина
()
≡
=
(2.19)
называется средним квадратическим отклонением случайной величины ξ.
Размерность среднеквадратичного отклонения такая же, как и у сл. величины ξ, размерность же дисперсии равна квадрату размерности сл. величины ξ; такое различие размерностей не очень удобно, потому и вводится среднее квадратичное отклонение.
Вычисляют дисперсию по формуле:
(2.20)
Пример 18. Вычислим дисперсию для сл. величины из примера 14:
Решение. D
=
.
Пример19. Вычислим дисперсию сл. величины из примера 15.
Решение.
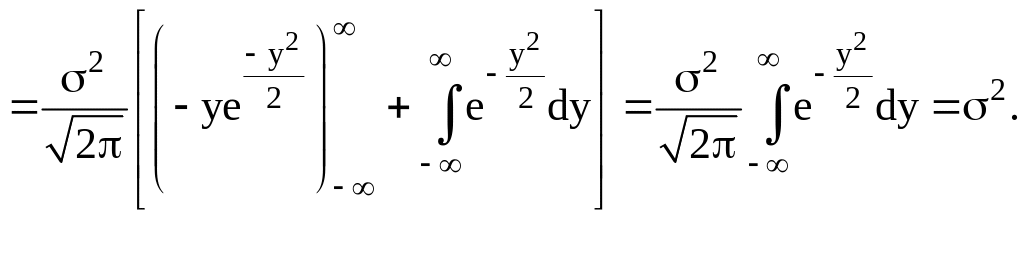
Из примера 19 видим, что вторым параметром в нормальном распределении является среднее квадратическое отклонение.
Свойства дисперсии.
D1.
если
.
D2.
.
D3.
,
если величины
независимы.
Рассмотрим выражение
По свойству математического ожидания
,
если
независимы – это с одной стороны; с
другой стороны
Следствия. 1)
;
2)
,
.
D4.
Действительно, рассмотрим равенства
Пример 20. Вычислить дисперсию сл. величины из примера 16.
Решение. Для
вычисления дисперсии сл. величины,
имеющей
–распределение,
воспользуемся свойством D4.
Из примера 16
возьмем величину
Замечание. Если сл. величина имеет математическое ожидание, то дисперсия всегда определена, но может принимать значение, равное ∞.
Пример 21. Пусть функция плотности распределения сл. величины ξ задана формулой
В точках –2, –1 и
2 функция f(x) имеет разрывы. Всем свойствам
плотности вероятностей функция
удовлетворяет, в частности,
–конечной дисперсии
нет.
Упражнение. Получить выражения для математических ожиданий и для дисперсий всех случайных величин, описанных выше в этом разделе, исключая распределение Вейбулла и гамма-распределение.
2.7. Моменты случайных величин. Другие числовые характеристики случайных величин
Математическое ожидание и дисперсия сл. величины являются представителями целого класса характеристик, которые называются моментами сл. величин.
Начальным моментом
порядка
cл.
величины
называется число:
(2.21)
При
математическое ожидание – начальный
момент 1-го порядка.
Центральным моментом порядка cл. величины называется число:
(2.22)
При
дисперсия сл. величины – это центральный
момент второго порядка. Интересно
отметить, что
Абсолютным
моментом порядка
сл. величины ξ называются число
.
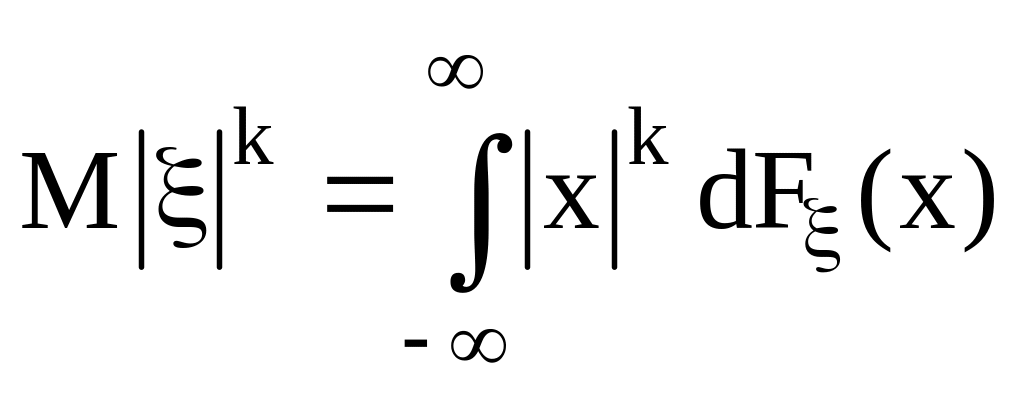Между начальными и центральными моментами существуют связывающие их соотношения, для последующих вычислений нам будут интересны только два:
(2.23)
Моменты служат в дополнение к математическому ожиданию и дисперсии для более детального изучения особенностей распределения сл. величины. Особенно важны моменты 3 и 4 порядков, так как через них выражаются некоторые числа (такие как асимметрия и эксцесс), характеризующие распределение сл. величин.
Таким образом, две характеристики положения, наиболее часто используемые для описания сл. величин, являются представителями широкого класса характеристик сл. величин – моментов сл. величин.
Из других
характеристик положения наиболее часто
используют медиану и моду случайной
величины, обозначают их символами
и Моξ соответственно.
Медиана
случайной величины ξ – число
–
определяется из соотношения
.
Из определения следует, что медиана сл.
величины – это любое решение уравнения
.
Поскольку решение этого уравнения не
единственно, то медиана сл. величины
определяется неоднозначно.
Модой непрерывной сл. величины ξ называют точку локального максимума ее плотности распределения f(x). По числу мод распределения бывают унимодальные (одна мода), бимодальные (две моды) и мультимодальные (более двух мод). Нормальное распределение, например, относится к числу унимодальных, причем Me=Моξ=m – математическому ожиданию.
Модой
дискретной
сл. величины называют такое её значение
,
для которого
и
,
при этом все её значения должны быть
расположены в порядке возрастания.
Пример 22.
Рассмотрим
сл. величину, имеющую распределение
Коши
Известно, что эта сл. величина не имеет
математического ожидания (см. пример
17). Однако функция f(х) имеет глобальный
максимум в точке х=0, f(0)=
.
Следовательно, Моξ = 0.
Широкое применение в математической статистике при построении доверительных интервалов и при проверке статистических гипотез находят α – квантили.
-квантилью
(симметричной
-квантилью)
сл. величины
называется
число,
удовлетворяющее
уравнениям:
(
).
Отметим, что
– это медиана случайной величины Me:
Пример 23. Найти -квантили и медиану экспоненциального распределения.
Решение.
.
Для первой проверки сл. величины на нормальность в математической статистике используют асимметрию и эксцесс.
Асимметрией
сл. величины
называется число
Если
для
любого х, то
так как в этом случае все центральные
моменты нечетных порядков равны нулю.
Равенство вероятностей означает, что
сл. величина распределена симметрично
относительно своего математического
ожидания.
Таким образом, коэффициент асимметрии служит для характеристики степени несимметричности функции плотности распределения сл. величины. Если >0, то функция плотности распределения по отношению к ее математическому ожиданию имеет сдвиг вправо; для <0 – влево.
Пример 24. Вычислить асимметрию для случайной величины, имеющей нормальный закон распределения.
Решение.
Поскольку 
вычислим составляющие этой формулы:
–интеграл от нечетной подынтегральная
функции по симметричному промежутку.
Тогда
.
Из примера следует, что нормальное распределение является своего рода эталоном, с которым сравниваются другие распределения.
Замечание.
При сравнении сл. величин их нужно
центрировать и нормировать, то есть от
сл. величины
переходить к сл. величине
.
Вновь полученные сл. величины имеют те
же значения
,
что и исходные.
Эксцессом
сл. величины
называется число
Эксцесс, как правило, используется для
характеристики симметричности
унимодальных распределений.
Пример 25. Для
нормального распределения
=0,
так как:
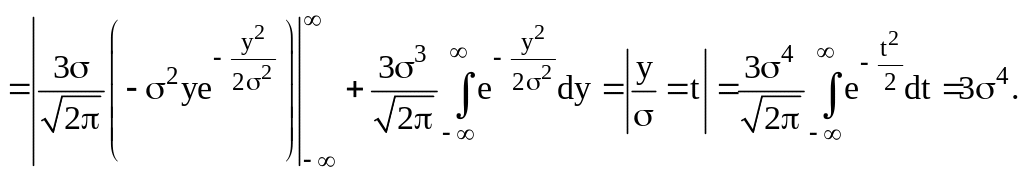
Если для некоторой сл. величины >0, то кривая плотности распределения более островершинна, чем при нормальном распределении; если <0, то кривая плотности распределения более плоская, чем при нормальном распределении. При этом справедливо замечание относительно преобразования сравниваемых сл. величин, сделанное выше. Более подробно эти вопросы можно изучить по специальной литературе по теории вероятностей и математической статистике.