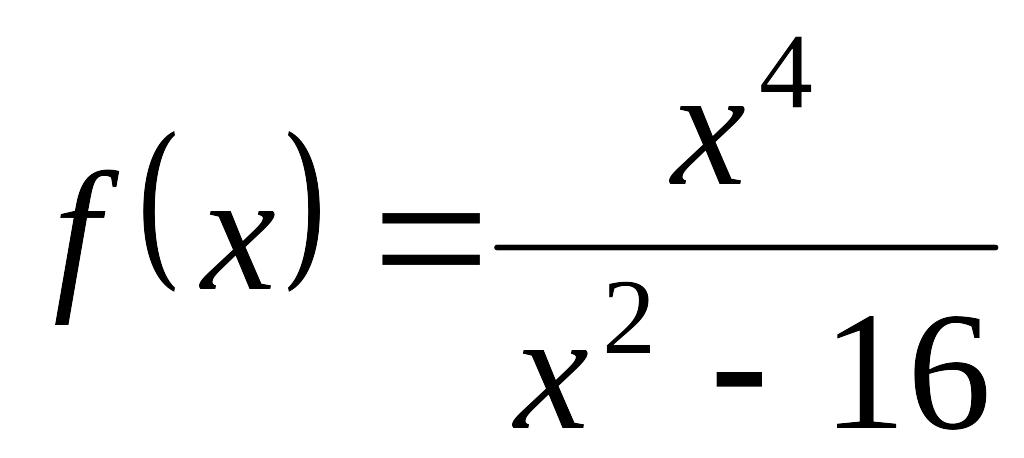Какие из следующих функций чётные, какие нечётные, а какие функции общего вида:
№ |
Пример функции |
Область определения |
Вид функции |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
Выберите верные утверждения:
№ |
Утверждение |
(+) () |
1 |
если f(x) – чётная, то её график симметричен относительно оси ординат |
|
2 |
если f(x) – не является чётной, то её график не симметричен относительно оси ординат |
|
3 |
если f(x) – не является чётной, то её график симметричен относительно оси ординат |
|
4 |
если f(x) – чётная, то её график симметричен относительно оси абсцисс |
|
5 |
если f(x) – не является чётной, то её график не симметричен относительно оси абсцисс |
|
6 |
если f(x) – не является чётной, то её график симметричен относительно оси абсцисс |
|
7 |
если f(x) – чётная, то её график симметричен относительно начала координат |
|
8 |
если f(x) – не является чётной, то её график не симметричен относительно начала координат |
|
9 |
если f(x) – не является чётной, то её график симметричен относительно начала координат |
|
10 |
если f(x) – нечётная, то её график симметричен относительно оси ординат |
|
11 |
если f(x) – не является нечётной, то её график не симметричен относительно оси ординат |
|
12 |
если f(x) – не является нечётной, то её график симметричен относительно оси ординат |
|
13 |
если f(x) – нечётная, то её график симметричен относительно оси абсцисс |
|
14 |
если f(x) – не является нечётной, то её график не симметричен относительно оси абсцисс |
|
15 |
если f(x) – не является нечётной, то её график симметричен относительно оси абсцисс |
|
16 |
если f(x) – нечётная, то её график симметричен относительно начала координат |
|
17 |
если f(x) – не является нечётной, то её график не симметричен относительно начала координат |
|
18 |
если f(x) – не является нечётной, то её график симметричен относительно начала координат |
|
19 |
существуют функции, являющиеся одновременно чётными и нечётными |
|
20 |
не существует функций, являющихся одновременно чётными и нечётными |
|