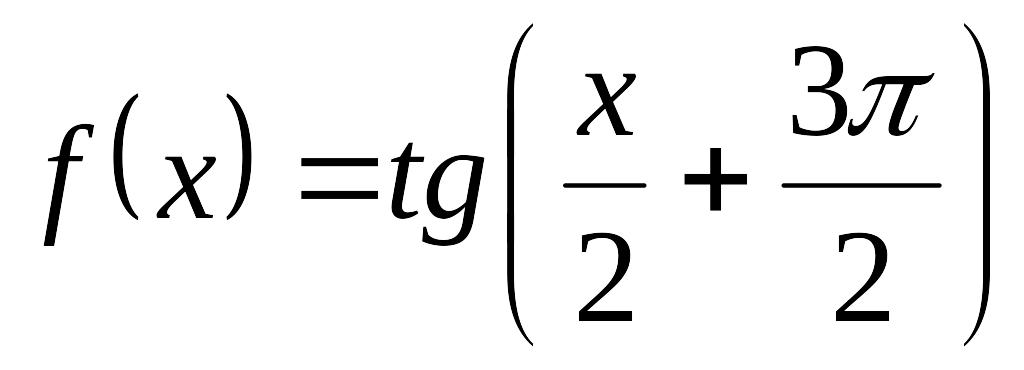- •Чётные и нечётные функции.
- •Продолжите утверждение:
- •Выберите среди предложенных функции, которые следует исследовать на чётность или нечётность:
- •Какие из следующих функций чётные, какие нечётные, а какие функции общего вида:
- •Периодические функции.
- •Известно, что функция f(X) – периодическая функция с периодом t. Запишите к каждой функции соответствующие им периоды:
- •Построить в полярной системе координат:
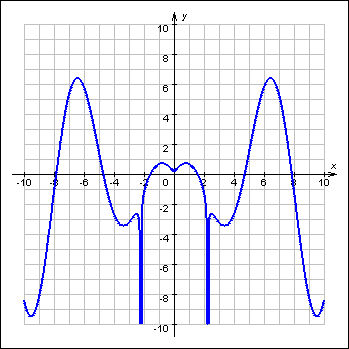
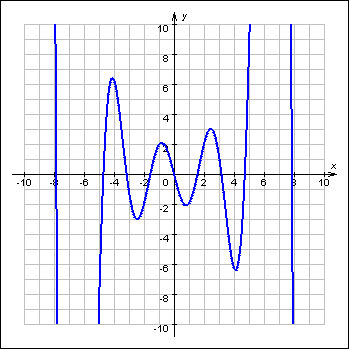
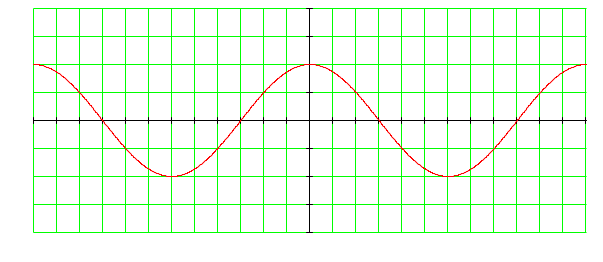
- •Соотнести функции и построенные графики:
- •Построить в прямоугольной декартовой системе координат функцию заданную параметрически:
- •Соотнести функции и построенные графики:
- •Разложение многочлена на множители. Теория.
Функции. Полярная система координат.________________________________________
Чётные и нечётные функции.
Функция у=f(х) называется чётной, если для любого х из области определения функции выполняется равенство f(-х)=f (x). |
у=f(х) чётная хD(y) f(-х)=f (x) |
Функция у=f(х) называется нечётной, если для любого х из области определения функции выполняется равенство f(-х)=-f (x). |
у=f(х) нечётная хD(y) f(-х)=-f (x) или у=f(х) нечётная хD(y) f(х)=-f (-x) |
Из определения следует, что область определения D(y) как чётной, так и нечётной функции должна обладать следующим свойством: если хD(y), то и -хD(y) (т. е. D(y) - симметричное относительно 0 множество). |
|
Функция у=f(х) которая не является ни чётной, ни нечётной называется функцией общего вида. |
|
Если функция является чётной, то её график симметричен относительно ________________________. Обратное утверждение _____________________.
Итак, функция является чётной тогда и только тогда, когда её график симметричен относительно оси Оу.
Если функция является нечётной, то её график симметричен относительно ________________________. Обратное утверждение _____________________.
Итак, функция является нечётной тогда и только тогда, когда её график симметричен относительно начала координат.
|
|
|
|
Сумма чётных (нечётных) функций является чётной (нечётной) функцией.
Произведение двух чётных или двух нечётных функций является чётной функцией.
Произведение чётной и нечётной функции является нечётной функцией.
Если функция f чётна (нечётна), то и функция 1/f чётна (нечётна).
Продолжите утверждение:
Известно, что функция f(x) – нечётная функция, причём в точке (х0; f(х0)) функция имеет минимум, и х2<x1<0, причём на интервале (х2; х1) функция возрастает.
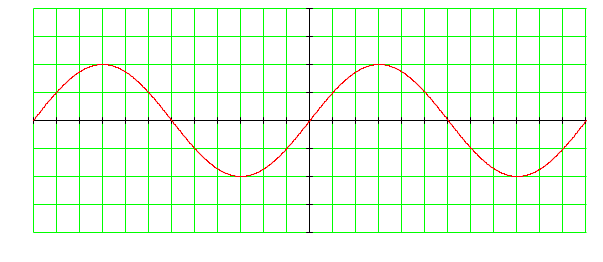
функция f(x) в точке (-х0; _____) имеет___________________;
функция f(x) в точке (-х0; _____) имеет___________________;
функция f(x) на интервале______________________________;
Известно, что функция f(x) – чётная функция, причём в точке (х0; f(х0)) функция имеет минимум, и х2>x1>0, причём на интервале (х1; х2) функция возрастает.
функция f(x) в точке (-х0; _____) имеет___________________;
функция f(x) в точке (-х0; _____) имеет___________________;
функция f(x) на интервале______________________________;
Выберите среди предложенных функции, которые следует исследовать на чётность или нечётность:
№ |
Пример функции |
Область определения |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|