
- •Лабораторная работа № 1
- •Условия однозначности включают:
- •I класс. Прямые задачи
- •2 Класс. Обратные задачи:
- •3 Класс. Инверсные задачи
- •4 Класс. Индуктивные задачи
- •Примерная форма журнала наблюдений
- •Лабораторная работа № 2
- •Примерная форма журнала наблюдений
- •Лабораторная работа № 3
- •Примерная форма журнала наблюдений
- •Лабораторная работа № 4
- •Из уравнений (14) или (15) определяется температура в сечении
- •Определение продолжительности выдержки
- •Лабораторная работа № 6
- •Лабораторная работа № 7
- •Примерная форма журнала наблюдений
- •Лабораторная работа №8
- •Окончательный результат записывается в виде
- •Программа статистической обработки экспериментальных данных
- •Физические свойства некоторых твердых тел (элементов) при 00с
- •Физические свойства некоторых жидких металлов
- •Коэффициент теплопроводности сталей в зависимости от температуры
- •Коэффициент теплопроводности некоторых сплавов
- •Приложение 8 Физические свойства технических материалов
- •Физические характеристики воды на линии насыщения
Примерная форма журнала наблюдений
№ замера |
Показания U-образного манометра, мм вод.ст. |
Температура, 0С
|
|
tвх |
tвых |
||
1. 2. 3. … … … |
|
|
|
1. 2. 3. … … … |
|
|
|
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ.
Коэффициент теплоотдачи от стенки трубы к воздуху определяется из выражения коэффициента теплопередачи при стационарном тепловом состоянии от воды к воздуху через стенку трубы:
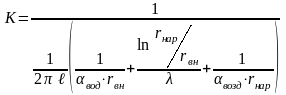 ,
,
где
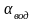 =
3500 Вт/(м2
К) - коэффициент теплоотдачи от воды к
наружной поверхности трубы;
=
3500 Вт/(м2
К) - коэффициент теплоотдачи от воды к
наружной поверхности трубы;
λ = 35 Вт/(м К) - коэффициент теплопроводности материала стенки;
rнар=11 мм; rвн=9 мм;
Коэффициент теплопередачи определяется из выражения
= K×Δtср · F, Вт,
где - тепловой поток передаваемый через боковую поверхность трубы от воды к воздуху
 ,
Вт,
,
Вт,
где V0 - расход воздуха, м3 /ч, определяемый по показаниям U-образного манометра и тарировочной кривой
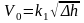 ,
k1=1,78
,
k1=1,78
СVж - средняя в интервале 0 – tж теплоемкость воздуха, Дж/м3 К;
tвых - средняя температура на выходе, 0С;
tж = 0,5 (tвх + tвых );
Δtср - средняя логарифмическая разность температур, 0С;
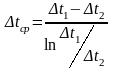

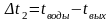
tвх - средняя температура на входе, 0С;
F - поверхность теплообмена, м2
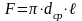
 -
средний диаметр трубы, м;
-
средний диаметр трубы, м;
ℓ- длина трубы.
Построение
зависимости
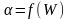
Скорость воздуха в трубе W определяется из выражения

где
 - поперечное сечение трубки, м2
.
- поперечное сечение трубки, м2
.
Полученные экспериментальным путем коэффициенты теплоотдачи необходимо сравнить с расчетными по формуле (10)
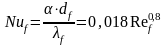
откуда
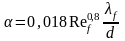
Теплофизические свойства воздуха приведены в приложении 2.
Дать статическую обработку полученных экспериментальных данных (Приложение 1).
УКАЗАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТА.
Отчет должен содержать основные теоретические положения, описание и схему установки, журнал наблюдений, обработку экспериментальных данных, графическую зависимость α = f(W) по опытным данным и по формуле (2), выводы по работе.
ТЕХНИКА БЕЗОПАСНОСТИ.
Включение и выключение установки производить под наблюдением преподавателя. Студенту разрешается пользоваться только ручками регулирования ЛАТРа. К остальным элементам установки прикасаться не разрешается.
Следует быть внимательным при нагреве воды в водяной рубашке, не допускать излишне интенсивного кипения во избежание выбросов пара из водяной рубашки.
Литература [1], [4].
Лабораторная работа № 4
ИССЛЕДОВАНИЕ ТЕПЛООТДАЧИ ГОРИЗОНТАЛЬНОЙ ТРУБЫ ПРИ СВОБОДНОЙ КОНВЕКЦИИ
ЦЕЛЬ РАБОТЫ.
Углубление знаний по теории конвективного теплообмена при свободной конвекции, знакомство с методикой постановки и проведения экспериментальных исследований, получение навыков в применении статистических методов обработки экспериментальных данных на ЭВМ.
ЗАДАНИЕ.
Определить зависимость коэффициента теплоотдачи при свободной конвекции от температурного напора.
Обработать экспериментальные данные и представить их в форме критериального уравнения.
Составить отчет и защитить его.
ОСНОВНЫЕ ПОЛОЖЕНИЯ.
При свободной конвекции движение среды возникает только под действием разности плотностей, связанной с неизотермичностью исследуемого объема. Различают три режима свободного движения среды около нагретого (охлаждаемого) тела: ламинарный, локонообразный и вихревой. Переход от одного режима к другому связан со степенью турбулизации пограничного слоя подвижной среды на теплообменной поверхности. Степень турбулизации пограничного слоя и, соответственно, интенсивность теплоотдачи в основном определяются разностью температур между теплообменной поверхностью и подвижной средой, а также линейными размерами тела, участвующего в теплообмене и слабо зависят от геометрической формы тела. Также как и при анализе вынужденной конвекции в математическом описании теплообмена при свободной конвекции используются уравнения:
- энергии подвижной среды;
- неразрывности;
- движения,
решение, которых совместно с условиями однозначности дает возможность получить значения α или в безразмерной форме

Поскольку движение среды при свободной конвекции обусловлено разностью плотностей, то в уравнение движения вместо массовой силы ρg должна быть введена термическая подъемная сила ρgβDt. Применение методов теории подобия позволяет получить общую форму решения в виде критериального уравнения:
Nu = f(Gr,Pr). (1)
Аналитическое определение функции f в общем виде затруднено, поэтому, как и при анализе вынужденной конвекции, в большинстве случаев ищется приближенное решение системы дифференциальных уравнений в критериальной форме
 ,
для сред с Pr ≥ 0,5; (2)
,
для сред с Pr ≥ 0,5; (2)
Nu = с2 (Pr2 ∙ Gr)m , для металлических жидкостей, (3)
где константы с1 , с2 , m, n могут определяться как аналитически, так и с использованием экспериментальных методов.
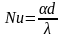 -
критерий Нуссельта характеризует
интенсификацию теплопереноса за счет
конвекции по сравнению чистой
теплопроводностью среды;
-
критерий Нуссельта характеризует
интенсификацию теплопереноса за счет
конвекции по сравнению чистой
теплопроводностью среды;
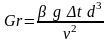 -
критерий Грасгофа характеризует
соотношение силы, вызывающей гравитационную
конвекцию и сил вязкого трения;
-
критерий Грасгофа характеризует
соотношение силы, вызывающей гравитационную
конвекцию и сил вязкого трения;
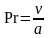 -
критерий Прандтля характеризует степень
соответствия скоростных и температурных
полей;
-
критерий Прандтля характеризует степень
соответствия скоростных и температурных
полей;
λ - коэффициент теплопроводности, Вт/(м К);
a - коэффициент температуропроводности, м2 /с;
ν - кинематический коэффициент вязкости, м2 /с;
β = 1/T – коэффициент объемного расширения газа, 1/К;
g = 9,81 м/с2 - ускорение силы тяжести.
Уравнение (1) безразмерно и поэтому пригодно для расчета коэффициента теплоотдачи для всех подобных систем.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.
Экспериментальная установка (рисунок 4.1) включает объект исследования, представляющий собой медную трубку 1 длиной ℓ = 1500 мм и наружным
диаметром d = 40 мм. Внутри трубы расположен электронагреватель 2. Внутреннее пространство между электронагревателем и трубой заполнено медными опилками для равномерного распределения тепла по длине трубы и устранения конвективных потоков.
По всей длине трубы на поверхности равномерно расположены 6 хромель-алюмелевых термопар 3 с угловым сдвигом 60. Холодные спаи термопар помещены в сосуд Дьюара 6 с тающим льдом. Подключение термопар к потенциометру 5 осуществляется через переключатель термопар 4. Электронагреватель подключается к сети переменного тока напряжением 220 В через лабораторный автотрансформатор (ЛАТР) – 7 , который предназначен для регулирования и поддержания подводимой мощности. Напряжение измеряется вольтметром 8. Включение и отключение всей установки производится выключателем 9.
ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ.
1.После ознакомления с инструкцией и подготовки журнала для записи экспериментальных данных получить у преподавателя разрешение на проведение работы.
2.Включение установки производится преподавателем или лаборантом.
3.При помощи ЛАТРа и вольтметра установить и поддерживать необходимую постоянную мощность на электронагревателе.
4.Измерения температур производить при строго установившемся тепловом режиме, который наступает через 30-40 мин. после включения установки, с интервалом 3-5 мин., в т.ч. 4-5 замеров при установившемся режиме.
5.Для перехода на новый тепловой режим надо изменить расход электроэнергии при помощи ЛАТРа. Через 30 мин. начать замеры, как в п.4.
Для выполнения работы в полном объеме необходимо провести опыты при 3-4 различных температурных режимах.
6.Температура воздуха измеряется термометром вдали от установки.
Примечания. Рекомендуется следующая последовательность установки режимов:
а) режим № 1. Установить напряжение 140 В. Через 15 мин. установить 110- 120 В и поддерживать это напряжение до конца опыта;
б) режим № 2. В целях ускорения охлаждения трубы установить напряжение 0-10 В. Через 15 мин. установить 80-90 В и поддерживать это напряжение до конца опыта;
в) режим № 3. Снять напряжение на 15 мин., затем установить 50-60 В;
г) режим № 4. Снять напряжение на 15 мин., затем установить 30-40 В.
Примерная форма журнала наблюдений
№ замера |
Напря-жение, U, В |
Температура стенки, 0С |
Температура воздуха в конце опыта, tв ,0С |
||||||||||||||||
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
tср |
|||||||||||||
1. 2. 3. … … |
|
|
|
|
|
|
|
|
|
||||||||||
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ.
Коэффициент теплоотдачи в каждом опыте определяется выражением
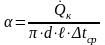 ,
Вт/(м2К), (3)
,
Вт/(м2К), (3)
где
d - диаметр трубки, м;
ℓ- длина трубки, м;
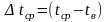 ;
;
tср - средняя температура стенки по 3-4 последним замерам;
tв - температура воздуха в конце опыта.
Тепловой поток, передаваемый трубкой путем конвекции, определяется из равенства:
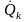 =
–
=
–
 , Вт,
, Вт,
где -тепловой поток снимаемый с нагревателя и передаваемый во внешнюю среду путем конвекции и излучения
= W, Вт,
где W - мощность, потребляемая электронагревателем,
,
где U - напряжение, В;
R = 28 Ом - сопротивление нагревателя;
- тепловой поток, передаваемый путем теплового излучения
 ,
Вт (5)
,
Вт (5)
где с - приведенный коэффициент излучения, Вт/(м2 К4);
F =πdℓ - поверхность трубки, м2 ;
Tс - температура стенки, К;
Tокр- температура окружающей среды, К.
Приведенный коэффициент излучения равен коэффициенту излучения опытной трубы, т.к. поверхность окружающих тел во много раз больше поверхности трубы. Для медной слабо полированной трубы
с= 1,0 Вт/(м2 К4 ).
При первичной обработке результаты опытов представляются графически в виде зависимости
α = f(Δt). (6)
Зависимость (6) строго справедлива для опытной трубы. Для распространения полученных результатов на весь класс подобных явлений (теплопередача свободной конвекции от горизонтальной трубы любых размеров в среду с любыми теплофизическими свойствами при любом температурном напоре) необходимо экспериментальные данные обобщить и представить в виде критериальной зависимости:
Nu = f(Gr Pr) (7)
Физические параметры воздуха (λ, a, ν, ρ) приведены в Приложении 3 и рассчитываются для температуры tср = 0,5(tс + tж ).
Вычисление критериев подобия производится для каждого температурного режима.
Полученные значения критериев наносят на график (в логарифмическом масштабе) lg Nu = lg (Gr Pr) и через точки проводят прямую. Уравнение этой прямой имеет следующий вид:
lg Nu = lg C + n lg (Gr Pr) (8)
Постоянная n определяется тангенсом угла наклона прямой к оси абцисс, а постоянная с находится из соотношения для любой точки прямой из уравнения
Nu = С(Gr Pr)n
 (9)
(9)
Уравнение (8) справедливо для подобных явлений в интервале измеренных значений произведения (Gr Pr).
Дать статистическую обработку полученных экспериментальных данных (приложение 1).
УКАЗАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТА.
Отчет должен содержать краткие теоретические положения, описание и схему установки, журнал наблюдений, расчеты α и график зависимости α = f(Δt), расчет и графическое построение критериальной зависимости Nu = f(Gr·Pr), выводы по работе.
ТЕХНИКА БЕЗОПАСНОСТИ.
Установка оборудована электронагревателем, приборами регулирования и измерения электрических параметров. Температура поверхности опытной трубы может находиться в интервале 50-250 0С, т.е. температура достаточна для образования ожогов.
При выполнении работы не прикасайтесь к опытной трубе и токоподводящим проводам.
Студентам разрешается пользоваться только рукоятками автотрансформатора и переключателя термопар.
Литература [1], [2],[3],[4].
ЛАБОРАТОРНАЯ РАБОТА №5
ИССЛЕДОВАНИЕ НЕСТАЦИОНАРНОГО ТЕПЛОВОГО РЕЖИМА
ПРИ ПОСТОЯННОЙ ТЕМПЕРАТУРЕ ПОВЕРХНОСТИ ОБРАЗЦОВ
1.ЦЕЛЬ РАБОТЫ
Знакомство с особенностями нагрева тел цилиндрической формы, с методикой постановки и проведения экспериментальных исследований при граничных условиях 1-го рода, с методикой расчета параметров поля температур; получение навыков в применении статистических методов обработки экспериментальных данных на ЭВМ.
2.ЗАДАНИЕ
Исследовать поле температур цилиндрического образца при нагреве с постоянной температурой поверхности.
Обработать экспериментальные данные и сравнить их с расчетными.
Составить отчет и защитить его.
3.ОСНОВНЫЕ ПОЛОЖЕНИЯ
В общем случае нестационарное поле температур определяется решением уравнения теплопроводности
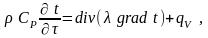 (1)
(1)
с соответствующими условиями однозначности.
При отсутствии внутренних источников и постоянных физических характеристиках из (1) следует
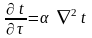 , (2)
, (2)
где
 - коэффициент температуропроводности.
- коэффициент температуропроводности.
В ряде важных практических приложений удается представить искомое решение в виде произведения двух функций от независимых переменных (метод Фурье - метод разделения переменных):
 (3)
(3)
Подстановка выражения (3) в уравнение теплопроводности (2) дает возможность разделить переменные
 (4)
(4)
Поскольку левая и правая части независимы друг от друга, а равенство должно удовлетворятся при любых сочетаниях x, y, z и t то они могут быть равны только в случае β2=const. Таким образом, решение уравнения в частных производных (2) удалось свести к решению системы двух дифференциальных уравнений
 (5)
(5)
 (6)
(6)
Решение уравнения (5) имеет простой вид
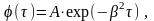 (7)
(7)
а после решения уравнения (6) можно найти решение задачи (2), используя выражение (3).
Общее решение (6) представляется как бесконечная сумма частных решений, функциональная структура которых определяется геометрией исследуемого тела. Например, для одномерной задачи распространения тепла имеем следующие структуры уравнения (6):
плоская
стенка 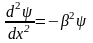 (8)
(8)
цилиндрическая
стенка
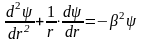 (9)
(9)
шаровой
слой 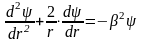 (10)
(10)
Функциональная структура получаемого решения определяется также формой условий однозначности:
- законом начального распределения температуры в исследуемом объеме;
- условиями внешнего теплообмена исследуемого тела (граничными условиями).
Строгая реализация в тепловом эксперименте граничных условий различных типов в общем случае довольно затруднительна. Однако, обеспечив определенные условия внешнего теплообмена и выбрав материал теплообменной поверхности с заданными свойствами, можно реализовать практически точно заданный тип граничных условий.
Рассмотрим принципиальную возможность реализации в тепловом эксперименте граничных условий 1-го рода (tn = const)
Пусть
поверхность W,
температура которой tw
и коэффициент теплопроводности λw
находится
в условиях конвективного теплообмена
с некоторой средой с температурой
tcp.
Тогда конвективный тепловой поток
α(tср-tw),
в соответствии с законом сохранения
энергии, должен равняться кондуктивному
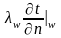 потоку.
На теплообменной поверхности отсутствуют
источники (стоки) тепла, т.е.
потоку.
На теплообменной поверхности отсутствуют
источники (стоки) тепла, т.е.
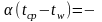 (11)
(11)
Если
ввести безразмерную координату
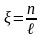 (ℓ
-
некоторый характерный размер исследуемого
тела), то (11) преобразуется к виду
(ℓ
-
некоторый характерный размер исследуемого
тела), то (11) преобразуется к виду
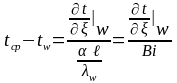 (12)
(12)
Переходя к пределу Bi→∞ из уравнения (12) получаем
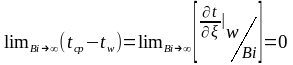 (13)
(13)
Таким образом, при реализации в тепловом эксперименте условия Bi→∞ на поверхности образца tw® tcp (случай кипящей воды - tcp=tH=tw=const). На практике при значениях Bi ≥100 можно принимать tw≈tcp.
Поскольку
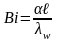 ,
обеспечить выполнение указанного
условия на практике можно с помощью
выбора материала теплообменной
поверхности с малым коэффициентом
теплопроводности λw
(эбонит, текстолит и т.д.) и режима
конвективного теплообмена с большим
значением a
(режима разовых превращений).
,
обеспечить выполнение указанного
условия на практике можно с помощью
выбора материала теплообменной
поверхности с малым коэффициентом
теплопроводности λw
(эбонит, текстолит и т.д.) и режима
конвективного теплообмена с большим
значением a
(режима разовых превращений).
4.ОПИСАНИЕ УСТАНОВКИ
Экспериментальная установка (рисунок 5.1) включает испытуемый образец 1, который помещен в сосуд 2, заполненный водой и закрытый крышкой 3. В образец по оси и на поверхности установлены две хромель-копелевые термопары 4, подключенные к многоточечному автоматическому потенциометру 5. Нагрев осуществляется с помощью электронагревателя 6, питаемого от напряжения 220 В. Подключение нагревателя осуществляется выключателем 7.
5. ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ
В сосуд 2 с кипящей водой погружается образец 3, с этого момента производится запись температур поверхности и центра образца с определенным интервалом, соответствующий дискретной записи температуры самозаписывающим потенциометром. Опыт продолжается до момента, когда
перепад температур между центром и периферией не будет превышать 3..5 0С. За начальную температуру образцов t0 принять температуру в лаборатории.
Результаты замеров заносятся в журнал наблюдений.
Примерная форма журнала наблюдений
№ п/п |
Время, с |
Температура, t, 0С |
Перепад температуры, ∆t |
||
поверхности |
центра |
||||
1 2 3 4 5 …
|
0
…
|
|
|
|
|
ВНИМАНИЕ! Погружение образца необходимо производить осторожно во избежание выплескиваний воды и получения ожогов.
6. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Расчетная часть
Различают несколько случаев аналитического решения уравнения (9) с граничными условиями I рода.
Первый случай. В начальный момент задано равномерное распределение температуры. На поверхности цилиндра температура мгновенно изменяется до величины tпов . решение для бесконечного цилиндра радиусом R имеет вид:

 (14)
(14)
где t - значение искомой температуры в точке с текущей координатой r/R;
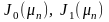 -
функции Бесселя первого рода нулевого
и первого порядка;
-
функции Бесселя первого рода нулевого
и первого порядка;
 -
безразмерная температура;
-
безразмерная температура;
Значение приведено на рисунке 5.2.
Второй случай соответствует параболическому распределению температуры в начальный момент. На поверхности цилиндра задается постоянная температура tпов .
Решение такой задачи для безразмерной температуры
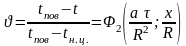 (15)
(15)
изображено на рисунке 5.3.
Обозначим
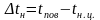
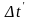 -
разность температур между поверхностью
и точкой имеющей координату r
-
разность температур между поверхностью
и точкой имеющей координату r

Полный
перепад температур
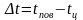 - может быть определен по рисунку 5.4.,
где представлена зависимость
- может быть определен по рисунку 5.4.,
где представлена зависимость
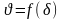
 .
.
В третьем случае начальное распределение температуры соответствует параболическому профилю, а температура поверхности цилиндра мгновенно изменяется.

Текущая температура определяется выражением
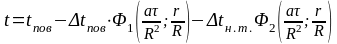 . (16)
. (16)
Определение температуры t образца для сечения с координатой r/R для заданного значения времени τ производится следующим образом.
Вычисляется критерий Фурье
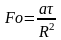
По критерию Фурье и значению безразмерной координаты r/R по графикам (рисунок 5.2 или 5.3) определяется значение функции Ф1 или Ф2.
