15, А проекция второго катета на гипотенузу равна 16.

Найдите диаметр окружности, описанной около

этого треугольника.

С

Дано:

АВС – прямоугольный,

СВ = 15, АН = 16

Найти: 2R

А Н В

Решение:

1) По теореме о пропорциональных отрезках в прямоугольном треугольнике

.

2) По теореме Пифагора

,

,

.

Пусть АВ = х, тогда

, ,

- не удовлетворяет условию задачи, поэтому АВ=25.

АВ=2R, так как гипотенуза прямоугольного треугольника есть диаметр

описанной около этого треугольника окружности.

Ответ: 2R=25.

-18-

Задача 7. Найдите диаметр окружности, описанной около

прямоугольного треугольника, если один из его

катетов равен 20, а проекция другого катета на

гипотенузу равна 9.

С Дано:

АВС – прямоугольный,

АС = 20, НВ = 9

Найти: 2R

А Н В

Решение:

1) По теореме о пропорциональных отрезках в прямоугольном треугольнике

АВС .

2) По теореме Пифагора

,

,

.

Пусть АВ = х, тогда

, ,

- не удовлетворяет условию задачи, поэтому АВ=25.

АВ=2R, так как центр описанной около прямоугольного треугольника

окружности лежит на середине гипотенузы этой окружности

Ответ: 2R=25.

-19-

Задача 8. В равнобедренный треугольник АВС вписана

окружность. Параллельно его основанию АС

проведена касательная к окружности, пересекающая

боковые стороны в точках D и Е. Найдите радиус

окружности, если DE = 8, АС = 18.

В Дано:

АВС – равнобедренный,

D E DE АС, DE = 8, АС = 18,

Найти: r

А С

Решение:

Способ первый.

1. АDЕС – равнобедренная трапеция, описанная около окружности. По

свойству описанного четырехугольника DЕ + АС = АD + ЕС, причем

АD = ЕС. Получим: 8+18=2АD, отсюда АD = ЕС = 13.

2) Пусть х = DВ = ВЕ, тогда АВ=ВС = х+13. DBE подобен ABC по

второму признаку подобия ( В – общий, ). Тогда их площади

относятся как произведения сторон, заключающих равные углы, и это

отношение равно квадрату коэффициента подобия:

, , ,

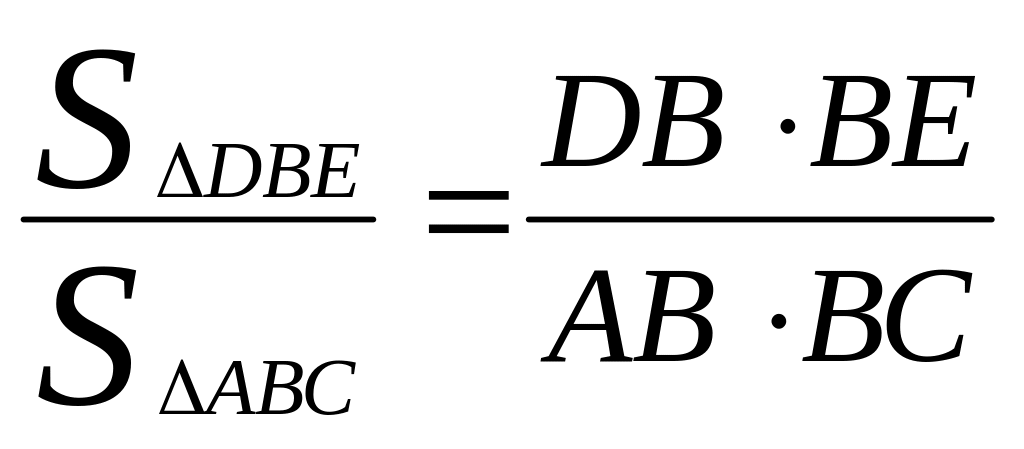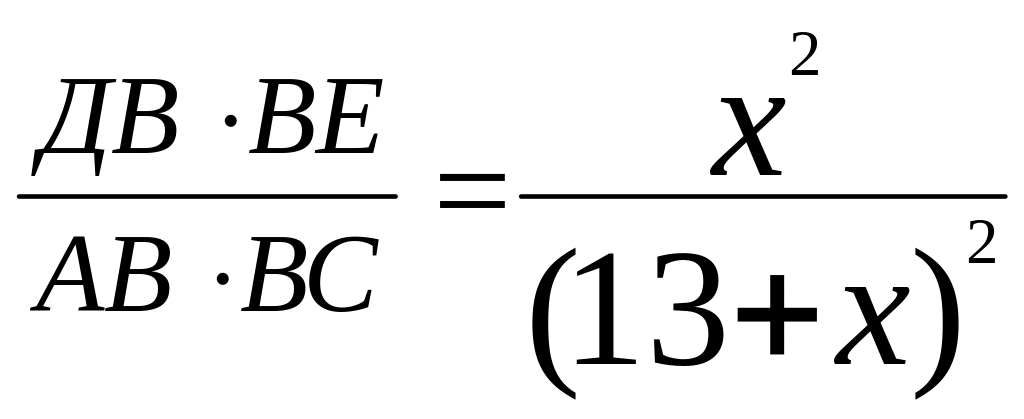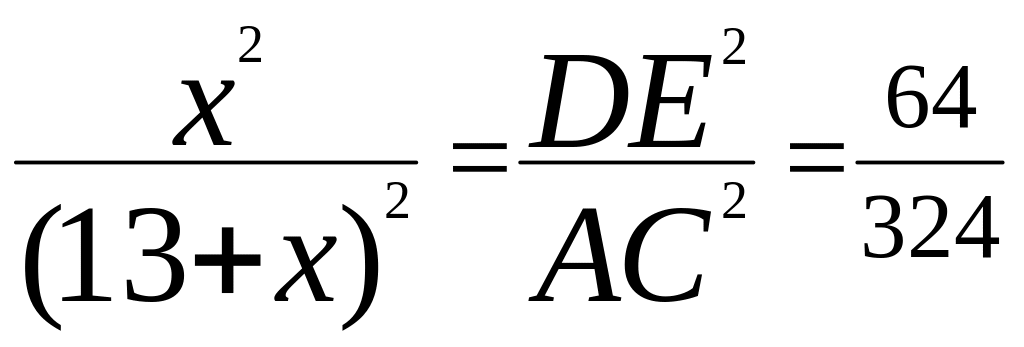:4

, , ,

- не удовлетворяет условию задачи, поэтому ВЕ = ВD=10,4.

Итак, ВЕ = ВD=10,4, АВ=ВС=23,4.

3) , . С одной стороны,

. С

другой стороны, или , тогда ,

откуда r = 6.

Ответ: r = 6.

-20-

Способ второй.

В

D E

А С

K

Решение:

1) А DЕС – равнобедренная трапеция, описанная около окружности (т.к.

DЕ АС и DЕ, АС, АD и ЕС – касательные к окружности). По

свойству описанного четырехугольника DЕ + АС = АD + ЕС, причем

АD = ЕС. Получим: 8+18=2 АD, отсюда АD = ЕС = 13.

2) Выполним дополнительное построение: проведем ЕК АD, тогда

АDЕК – параллелограмм, значит АD = ЕК = 13, DЕ = АК (по свойству

параллелограмма), тогда КС = АС – АК=18 – 8 = 10.

3) , , .

С одной стороны, ,

с другой стороны, или . Тогда ,

откуда h=12.

4) Так как высоты трапеции АDЕС и треугольника КЕС совпадают, то

h = 2r, r = 6.

Ответ: r = 6.

-21-

Способ третий.

В

D E

Q S

А С

K H

Решение:

2. А ДЕС – равнобедренная трапеция, описанная около окружности (т.к. ДЕ АС и ДЕ, АС, АД и ЕС – касательные к окружности). По

свойству описанного четырехугольника ДЕ + АС = АД + ЕС, причем

АД = ЕС. Получим: 8+18=2 АД, отсюда АД = ЕС = 13.

3. Выполним дополнительное построение: проведем высоту ВН и отрезок DK, DK АС.

4. Так как АВС – равнобедренный, ВН – высота, то ВН и медиана. Тогда АН = НС = 9.

5. АН = АQ=9 и НС = ЕС = 9, DQ = DL = 4 и LE = ES = 4

(DQ = AD – AQ = 13 – 9), как отрезки касательных, проведенных из

одной точки к окружности, где Q и S – точки касания АВ и ВС с

окружностью.

6. DL = KH = 4, DK = LH как противоположные стороны прямоугольника KDLH.

7. Рассмотрим ADK. АК = АН – КН = 9 – 4 = 5, АD = 13. По следствию из теоремы Пифагора , , отсюда

DK= LH = 12, причем LH=2r, тогда r = 6.

Ответ: r = 6.

-22-

Задача 9. В равнобедренный треугольник АВС с основанием

АС вписана окружность с центром О. Луч СО

пересекает сторону АВ в точке К, причем АК = 6,

ВК = 12. Найдите периметр треугольника.

Способ первый.

В

Дано:

АВС, АВ = ВС

АК = 6, ВК = 12, СО АВ = К

К Найти:

А С

Решение:

1. Так как окружность вписана, и О 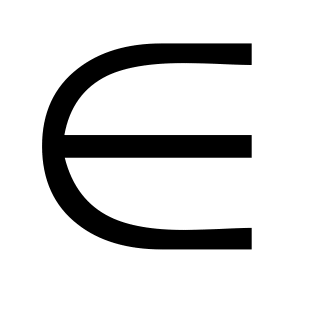КС (О – центр вписанной

окружности), то КС – биссектриса угла С. По свойству биссектрисы

(биссектриса делит сторону треугольника на части, пропорциональные

прилежащим сторонам) , или

(АВ = ВС = АК + КВ = 6+12 = 18), отсюда АС = 9.

2) = АВ + ВС + АС, = 18 + 18 + 9 = 45.

Ответ: = 45.

Способ второй.

Решение:

Так как СК – биссектриса угла С, то по теореме об отношении площадей треугольников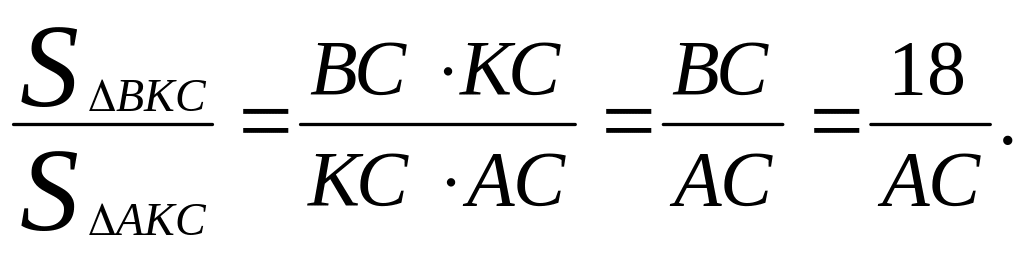 С другой стороны, это отношение равно (как отношение площадей треугольников, имеющих одинаковую высоту, опущенную из вершины угла С).

Итак, , откуда АС = 9 и = 45.

Ответ: = 45.

-23-

Задача 10. Около треугольника АВС описана окружность.

Медиана треугольника АМ продлена до пересечения

с окружностью в точке К. Найдите сторону АС, если

АМ=18, МК=8, ВК=10.

Дано:

В АВС, АМ – медиана,

К АМ =18, МК = 8, ВК = 10

Найти: АС

А С

Решение:

Способ первый.

1) Рассмотрим ВМК и АМС. ВМК = АМС, как вертикальные,

КВС = КАС, как вписанные углы, опирающиеся на одну дугу КС.

Тогда ВМК и АМС подобны по первому признаку подобия.

2) Из подобия треугольников следует, что или , но

ВМ = МС по условию, тогда , -

не удовлетворяет условию задачи, поэтому МС = 12. Тогда ,

отсюда АС = 15.

Ответ: АС = 15.

-24-

Способ второй.

Решение:

1) По теореме о пересекающихся хордах , ,

но ВМ = МС по условию (АМ – медиана), тогда , отсюда

ВМ = МС=12.

2) Рассмотрим ВМК и АМС. ВМК = АМС, как вертикальные,

ВМ = МС по условию. КВС = КАС, как вписанные углы,

опирающиеся на одну дугу КС. Тогда, ВМК и АМС подобны по

первому признаку подобия.

3) Из подобия треугольников следует, что , , отсюда

АС = 15.

Ответ: АС = 15.

-25-

Задача 11. Дан ромб ABCD. Окружность, описанная около

треугольника ABD, пересекает большую диагональ

ромба АС в точке Е. Найдите СЕ, если АВ = ,

BD = 16.

А Дано:

ABCD – ромб,

АВ = , BD = 16

Найти: СЕ

D В

С

Решение:

Способ первый.

1. По свойству ромба диагонали в точке пересечения делятся пополам,

поэтому ВО = ОD = 8.

2. Рассмотрим АОВ. АОВ – прямоугольный, поэтому по следствию из теоремы Пифагора или ,

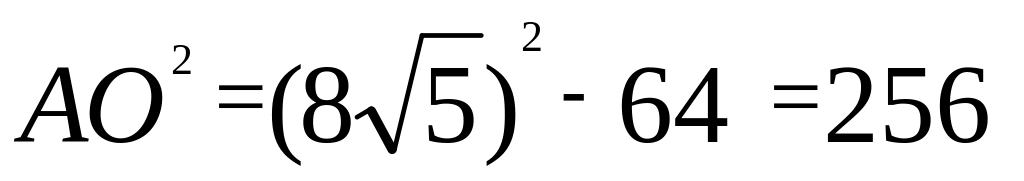отсюда АО = ОС=16, АС = АО + ОС = 32.

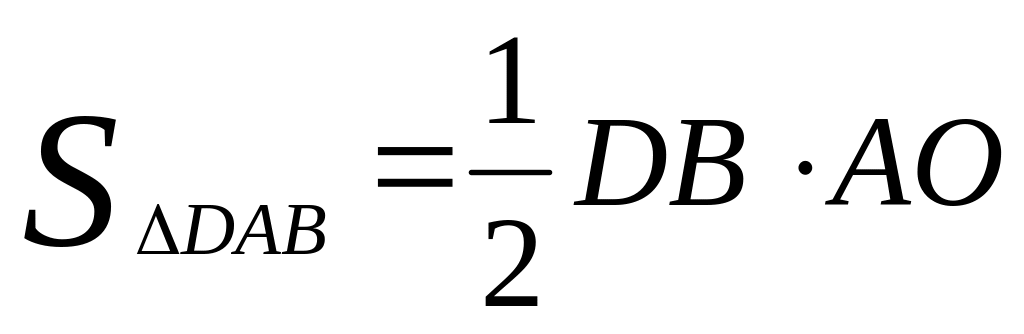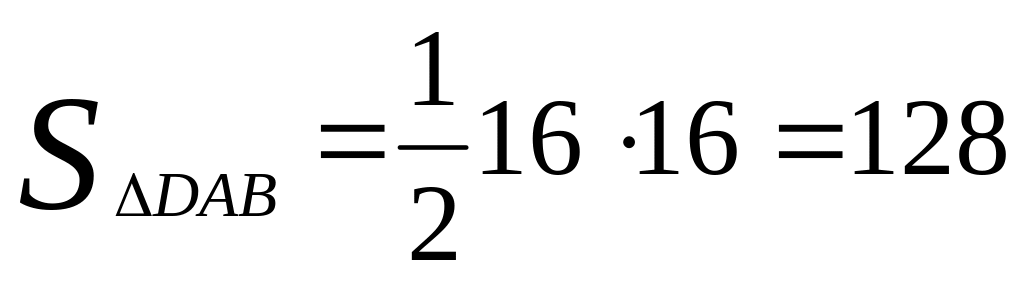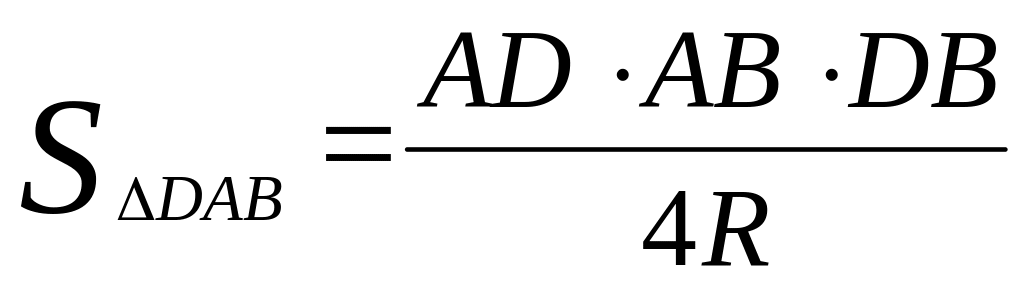3. С одной стороны, или , с другой стороны , где R – радиус описанной окружности, . Тогда 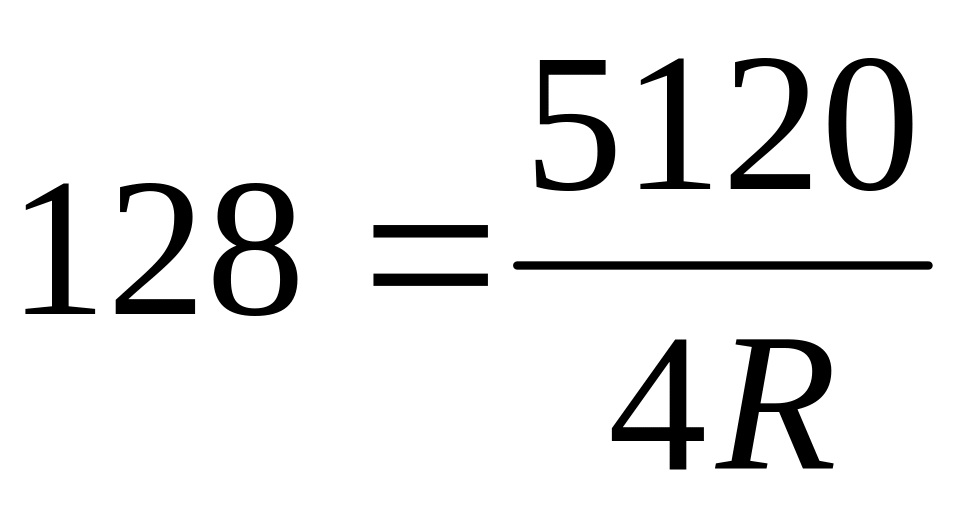, отсюда R = 10.

4. АЕ – диаметр окружности, АЕ = 2R = 20, АС = АО + ОС = 32, тогда

СЕ = АС – АЕ = 32 – 20 = 12.

Ответ: СЕ = 12.

-26-

Способ второй.

Решение:

1. Рассмотрим АDB. АDB – равнобедренный (AD = AB, как стороны ромба), АО – высота (поскольку диагонали ромба взаимно перпендикулярны), а, значит, и медиана и биссектриса (по теореме о высоте равнобедренного треугольника). По формуле нахождения медианы треугольника 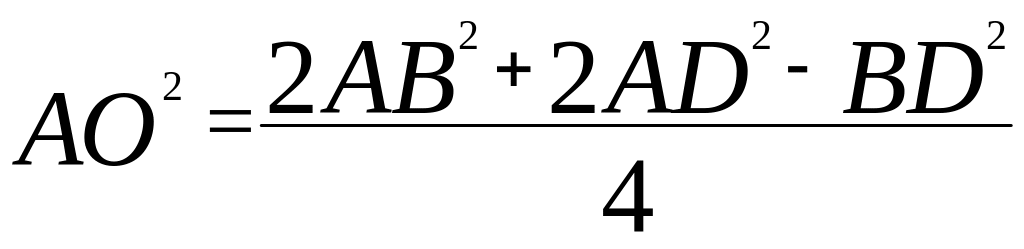, , 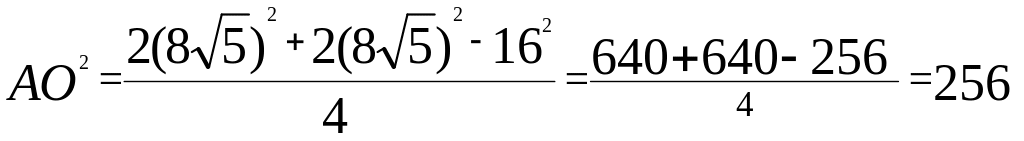откуда АО = 16.

2. С одной стороны, или , с другой стороны , где R – радиус описанной окружности, . Тогда , отсюда R = 10.

3. АЕ – диаметр окружности, АЕ = 2R = 20, АС = АО + ОС = 32, тогда

СЕ = АС – АЕ = 32 – 20 = 12.

Ответ: СЕ = 12.

Способ третий.

Решение:

5. 1) По свойству ромба диагонали в точке пересечения делятся пополам,

поэтому ВО = ОD = 8.

6. Рассмотрим АОВ. АОВ – прямоугольный, поэтому по следствию из теоремы Пифагора или ,

отсюда АО = ОС=16, АС = АО + ОС = 32.

3) По теореме о пересекающихся хордах , отсюда

. Тогда СЕ = СО – ОЕ = 16 – 4 = 12.

Ответ: СЕ = 12.

-27-

Задача 12. В окружность радиуса вписан треугольник АВС,

в котором , а сторона АВ в два раза больше

стороны АС. В треугольнике проведена

биссектриса АМ. Найти длину отрезка МС.

С Дано:

АВС, R = , ,

АВ = 2 АС, АМ – биссектриса

Найти: МС

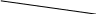
А

В

Решение:

Способ первый.

1) Поскольку АМ – биссектриса АВС, то по свойству биссектрисы угла

или или , отсюда ВМ = 2МС, тогда ВС = 3МС

или МС = ВС.

2) По следствию из теоремы синусов , отсюда .

Тогда МС = = 4.

Ответ: МС = 4.

-28-

Решение:

Способ второй.

1. Докажем, что АВС – прямоугольный. По теореме косинусов

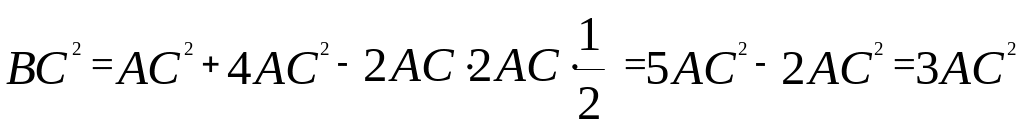. Предположим

справедливость равенства: , ,

- верное равенство, следовательно,

и АВС – прямоугольный.

2) Так как АВС – прямоугольный, АВ – гипотенуза, то АВ = 2R =

(поскольку центр описанной окружности лежит на середине

гипотенузы, т.е. АВ – диаметр). по условию, тогда

АС = . По следствию из теоремы Пифагора ,

, тогда ВС = 12.

3) Поскольку АМ – биссектриса, то по свойству биссектрисы угла

, где ВМ = СВ – СМ = 12 - СМ. , отсюда

, , СМ = 4.

Ответ: СМ = 4.

-29-

Задача 13. В треугольнике ВСЕ , СЕ : ВС = 3 : 1. Отрезок

СК – биссектриса треугольника. Найдите КЕ, если

радиус описанной около треугольника окружности

равен .

С Дано:

ВСЕ,

СЕ : ВС = 3 : 1,

СК – биссектриса

R =

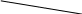
В Найти: КЕ

Е

Решение:

1) Поскольку СК – биссектриса СВЕ, то по свойству биссектрисы угла

или (так как по условию ), отсюда КЕ = 3ВК.

2) По теореме синусов , где ВЕ = 4ВК , отсюда ,

ВК = 6. Так как КЕ = 3ВК, то КЕ = 18.

Ответ: КЕ = 18.

-30-

Задача 14. В треугольнике АВС проведена медиана АМ.

Найдите площадь треугольника АВС, если

АС = , ВС = 10, .

В

Дано:

М АВС, АМ – медиана,

АС = , ВС = 10,

.

Найти:

А С

Решение:

1) Так как АМ – медиана, то ВМ = МС = 5.

2) По теореме косинусов в АМС

Пусть АМ = х, тогда

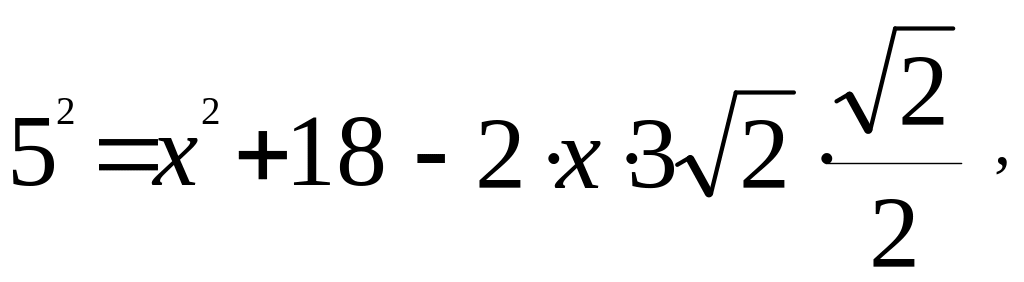
х = -1 – не удовлетворяет

условию задачи, х = 7. Итак, АМ = 7. ,

3) , так как треугольники имеют равные основания (ВМ = МС) и

высоту. Значит,

Ответ: 21.

-31-

Задача 15. Точка Н лежит на стороне АО треугольника АОМ.

Известно, что АН = 4, ОН = 12, , .

Найдите площадь треугольника АНМ.

Дано:

О АОМ, АН = 4, ОН = 12,

, .

Н Найти:

А М

Решение:

1) АНМ и АОМ подобны по первому признаку подобия

( по условию, А – общий), тогда или ,

тогда , АМ = 8.

2) , .

Ответ: 8.

-32-

Задача 16. В треугольнике ОВН точка М делит сторону ОВ на

отрезки ОМ = 4 и МВ = 28, . Найдите

площадь треугольника ОНМ, если .

Дано:

В ОВН, ОМ = 4, МВ = 28,

,

Найти:

М

О Н

Решение:

1) ОНМ и ОВН подобны по первому признаку подобия

( по условию, В – общий), тогда или ,

тогда , ОН = .

2) , .

Ответ: 128.

-33-

Задача 17. В треугольнике СЕН , точка Т делит сторону

СЕ на отрезки СТ = 2 и ЕТ = 14, .

Найдите площадь треугольника СНТ.

С

Дано:

Т СЕН,

СТ = 2, ЕТ = 14,

Найти:

Е Н

Решение:

1) СНТ и СЕН подобны по первому признаку подобия ( по

условию, С – общий), тогда или , тогда ,

СН = .

2) , .

Ответ: 4.

-34-

Задача 18. Точка К лежит на стороне АВ треугольника АВО, ВК = 12,

АК = 4, , cos . Найдите площадь

треугольника ОВК.

В Дано:

АВО, ВК = 12, АК = 4,

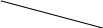К , cos

Найти:

А О

Решение:

1) КОВ и ВАО подобны по первому признаку подобия (

по условию, В – общий), тогда или , тогда

, ВО = .

2) , (по следствию из основного

тригонометрического тождества), или , тогда

Sin B = . .

Ответ: 48.

-35-

Задача 19. Найдите расстояние от точки пересечения медиан

прямоугольного треугольника до его гипотенузы,

равной 25, если один из катетов равен 20.

А Дано:

АВС – прямоугольный,

ВС=20, АВ =25,

Е AF, CE, BD - медианы

D К Найти: LK

С F В

Решение:

1. Так как медианы треугольника точкой пересечения делятся в отношении 2 : 1, считая от вершины, то AL=2LF, CL=2LE, BL=2LD.

2. По следствию из теоремы Пифагора .

3. , .

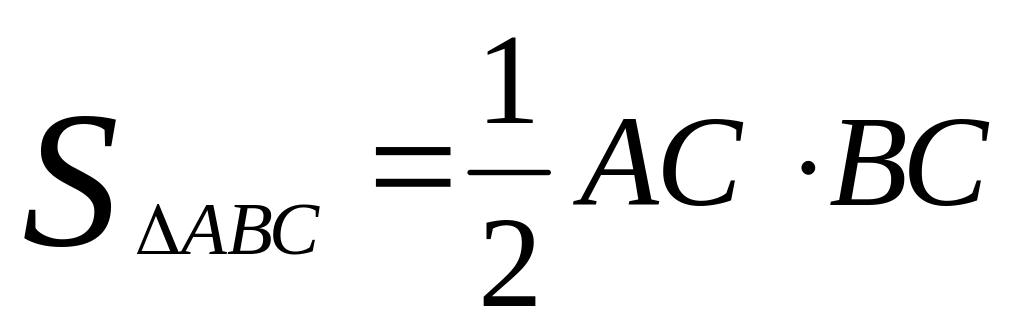4. Так как медианы треугольника делят его на шесть равновеликих треугольников, .

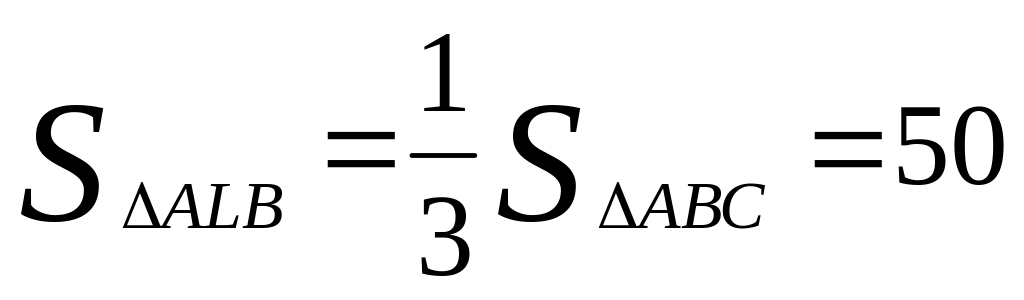5. , . Из равенства , получаем, что LK=4.

Ответ: LK=4.

-36-

Задача 20. Боковая сторона равнобедренной трапеции равна

, а основания равны 3 и 4. Найдите диагональ

трапеции.

В С Дано:

АВСD – равнобедренная

трапеция, АВ=CD= ,

ВС = 3, AD = 4

Найти: АС

А М Н D

Решение:

Способ первый.

1. Выполним дополнительное построение: проведем высоты СН и ВМ. Очевидно, что .

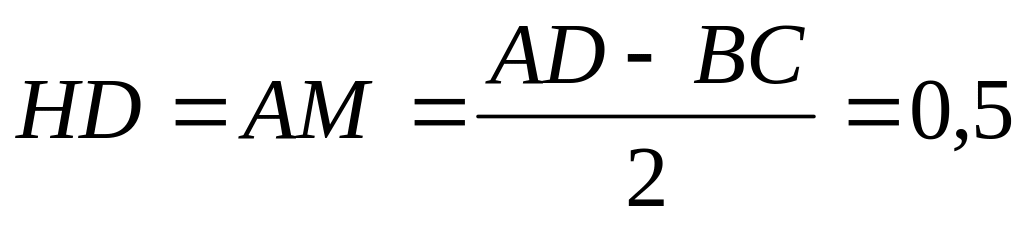2. : , , отсюда

СН = .

3) АНС – прямоугольный, поэтому по теореме Пифагора

, где АН = МН + АМ = 3 + 0,5 = 3,5.

, откуда АС = 5.

Ответ: АС = 5.

-37-

В С

А D

Способ второй.

Решение:

По теореме косинусов (из АВС) и (из АСD), тогда

;

, отсюда следует, что АС = 5.

Ответ: АС = 5.

-38-

Задача 21. Найдите площадь равнобедренной трапеции,

описанной около окружности с радиусом 4, если

известно, что боковая сторона трапеции равна 10.

К Дано:

В С ABCD - равнобедренная

трапеция, r = 4,

AB = CD = 10

Найти:

А D

Н М

Решение:

Способ первый.

1. Так как ABCD – описанная около окружности трапеция, то по свойству описанного четырехугольника ВС + АD = AB + CD, ВС + АD = 20, так как по условию AB = CD = 10.

2. Высота СМ = КН = 2r, (СМ = КН , как противоположные стороны прямоугольника НКСМ), или h = 8.

3. , .

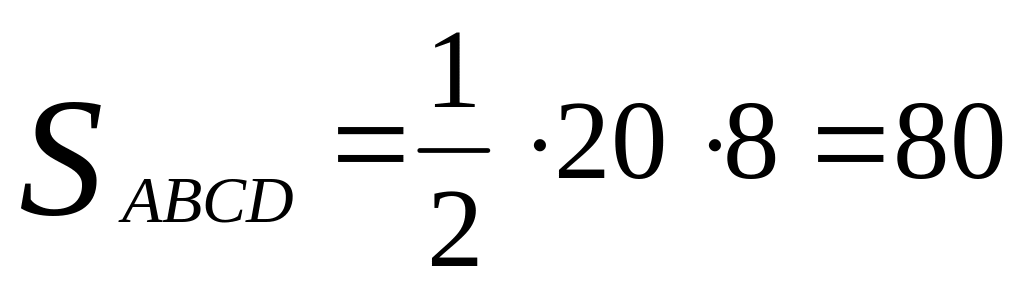Ответ: 80.

Способ второй.

Так как ABCD – описанная около окружности трапеция, то по свойству описанного четырехугольника ВС + АD = AB + CD, ВС + АD = 20. Тогда и .

Ответ: 80.

-39-

Задача 22. Точка М лежит внутри равнобедренного

треугольника АВС с основанием АС на расстоянии