
- •I. Треугольники
- •1) Теорема синусов.
- •2) Теорема косинусов.
- •3) Теорема о биссектрисе угла в треугольнике.
- •4) Вычисление биссектрисы угла.
- •5 ) Вычисление координаты точки отрезка.
- •4 ) Теорема об отрезках пересекающихся хорд.
- •15, А проекция второго катета на гипотенузу равна 16.
- •6 От боковых сторон и на расстоянии от
- •8, Боковая сторона 9, а диагональ 11. Найдите
Министерство образования Российской Федерации
Учебное пособие
«Решение задач
планиметрии. Практикум».
Автор: Евграфова Юлия Николаевна
г. Комсомольск – на – Амуре,
ул. Московская 22-25, тел. 25-68-22
ученица 10 А класса МОУ Лицей № 1
Адрес учреждения: г. Комсомольск – на – Амуре,
ул. Пирогова, 21, тел. 59-82-60
Научный руководитель: Будлянская Наталья Леонидовна
г. Комсомольск – на – Амуре,
ул. Вокзальная 72-71, тел. 59-95-03
преподаватель математики
2008 г.
-1-
Тезисы к работе
«Решение задач планиметрии. Практикум».
Многие мои сверстники не любят и боятся задач по планиметрии, а между тем они очень разнообразны, интересны и многие даже красивы. Надо только знать хорошо весь теоретический материал и владеть некоторыми приемами в подходах к решению такими, как выражение площади фигуры различными способами, выполнение дополнительных построений, использование тригонометрических функций, алгебраического аппарата и так далее.
Наиболее интересными, на мой взгляд, задачами являются такие, которые допускают многообразие способов их решения. И в этом плане мне понравились задачи, помещенные в сборнике Министерства образования «Единый государственный экзамен» 2003 – 2004 гг. Я создала к этой главе сборника своеобразный решебник, представив к большинству задач по 2-3 способа их решения и думаю, что мое пособие будет интересным и полезным в работе не только ученикам, но и учителям, осуществляющим подготовку их к экзаменам. Надеюсь, что вы со мною согласитесь.
-2-
Основные факты планиметрии.
I. Треугольники
1) Теорема синусов.
В треугольнике стороны пропорциональны синусам противолежащих
углов.
В

 а
b
а
b
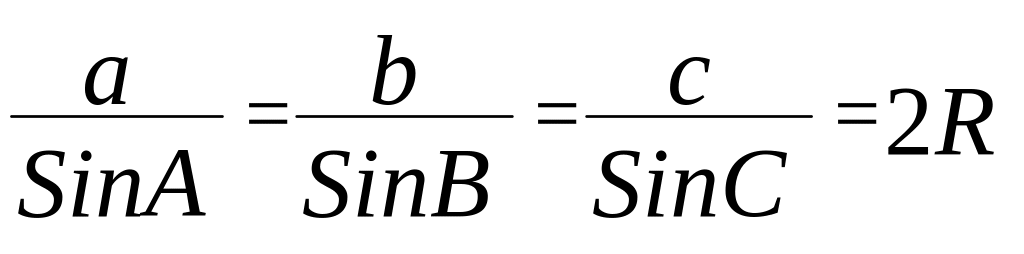
А
 c
С
c
С
2) Теорема косинусов.
В треугольнике квадрат одной стороны равен сумме квадратов двух других
сторон без удвоенного произведения этих сторон на косинус угла между
ними.
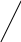

В
![]()
![]()
а
b
А с С
Примечание.
Если CosA![]() 0,
то
0,
то ![]() А
– острый, если CosА
= 0, то
А
– острый, если CosА
= 0, то
А
– прямой, если CosA
![]() 0,
то
А
– тупой.
0,
то
А
– тупой.
3) Теорема о биссектрисе угла в треугольнике.
Биссектриса угла треугольника делит его сторону на части,
пропорциональные прилежащим сторонам.



 В
В
 D
D
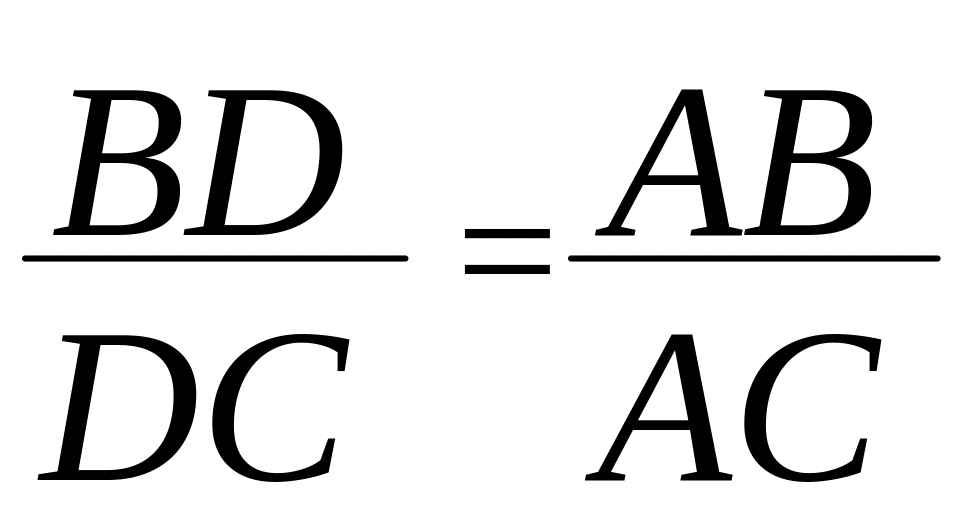
 А С
А С
4) Вычисление биссектрисы угла.


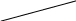 В
В

 А
С
А
С

-3-
5 ) Вычисление координаты точки отрезка.
С В
А
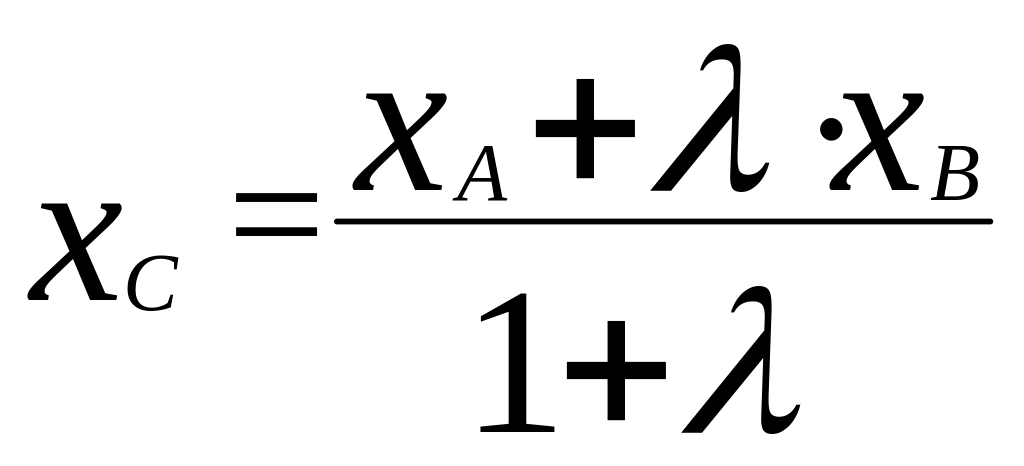 ,
где
,
где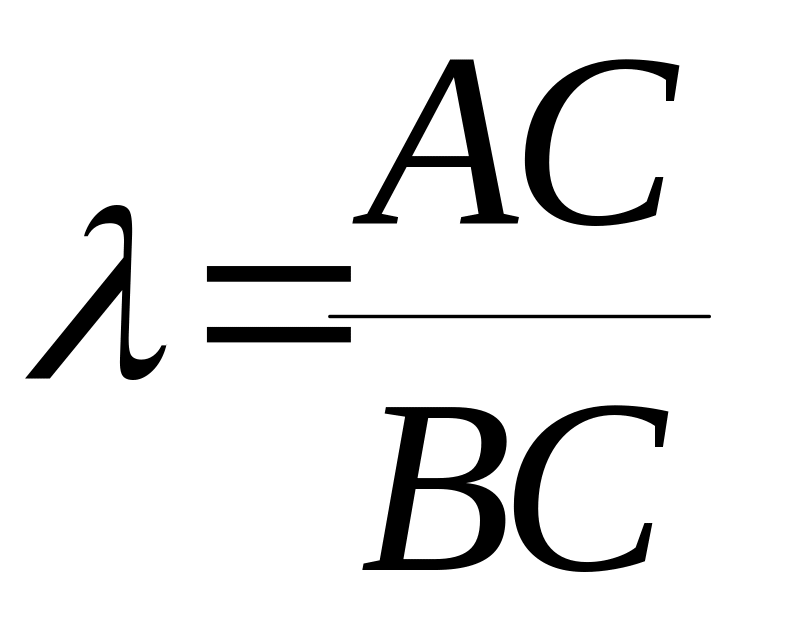 или
или
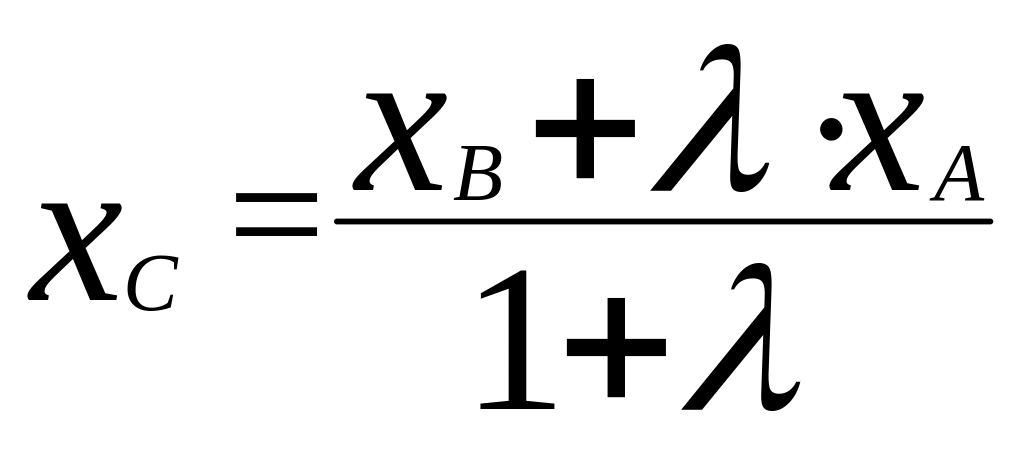 ,
где
,
где
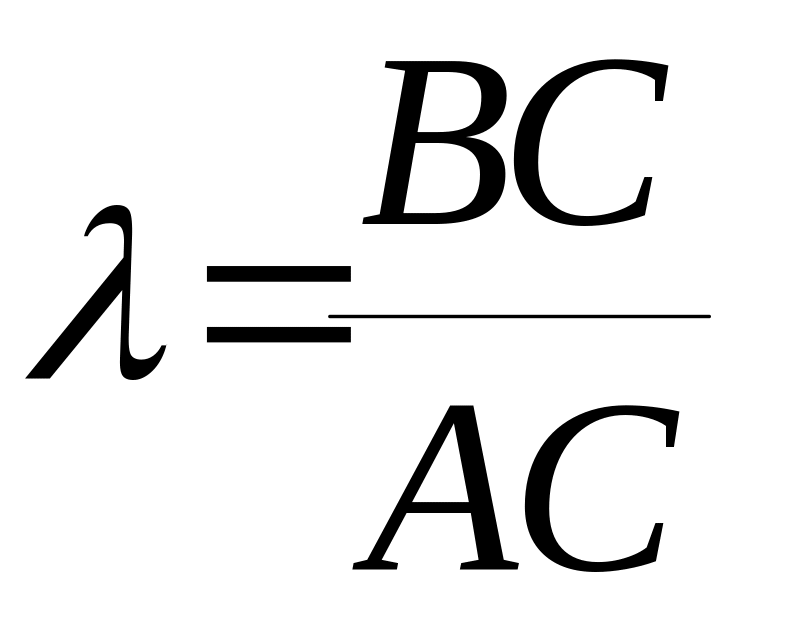
6) Теорема о медианах.
В треугольнике медианы пересекаются в одной точке и делятся в
отношении 2:1, считая от вершины.
В








![]()
![]()
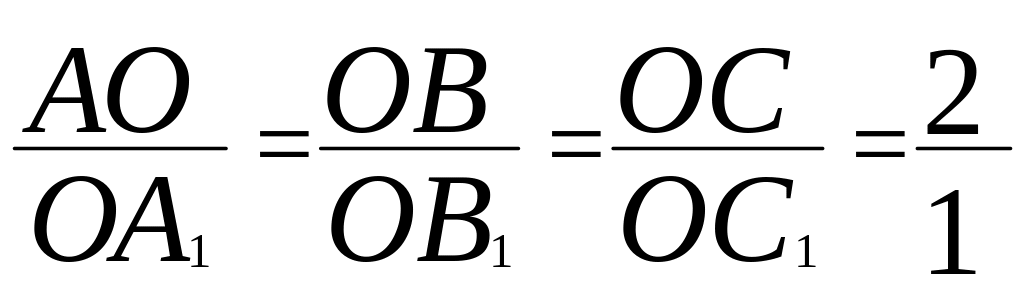
А
![]() С
С
7) Вычисление длины медианы треугольника
 С
С
с
![]() а
а 
А b В
8) Теорема о высоте прямоугольного треугольника.
С


 b
a
b
a
![]() ,
где
,
где
![]() =DB
– проекция катета а
=DB
– проекция катета а
 на
гипотенузу с,
на
гипотенузу с,
![]() =АD
– проекция
=АD
– проекция
А c В катета b на гипотенузу с.
D
![]() ,
,
![]()
9) Теорема о центре вписанной окружности.
В


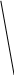 Центр
вписанной окружности лежит на
Центр
вписанной окружности лежит на
 пересечении
биссектрис треугольника.
пересечении
биссектрис треугольника.







 А
С
А
С
-4-
10) Теорема о центре описанной окружности.
Центр описанной окружности лежит на пересечении серединных
Перпендикуляров к сторонам треугольника.
Центр описанной окружности в остроугольном треугольнике лежит внутри треугольника;
Центр описанной окружности в тупоугольном треугольнике лежит вне треугольника;
Центр описанной окружности в прямоугольном треугольнике лежит на середине гипотенузы.
11) Тригонометрические функции в прямоугольном
треугольнике.
 А
А
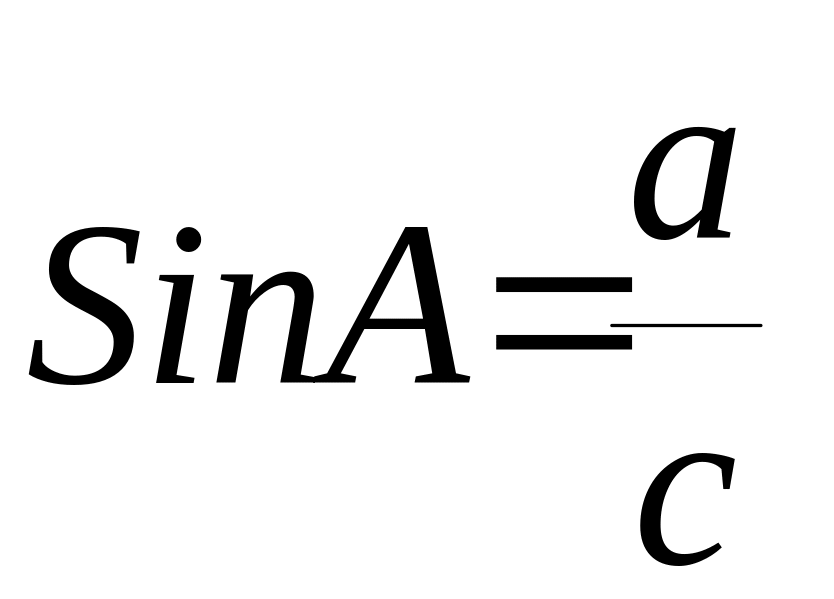 ,
,
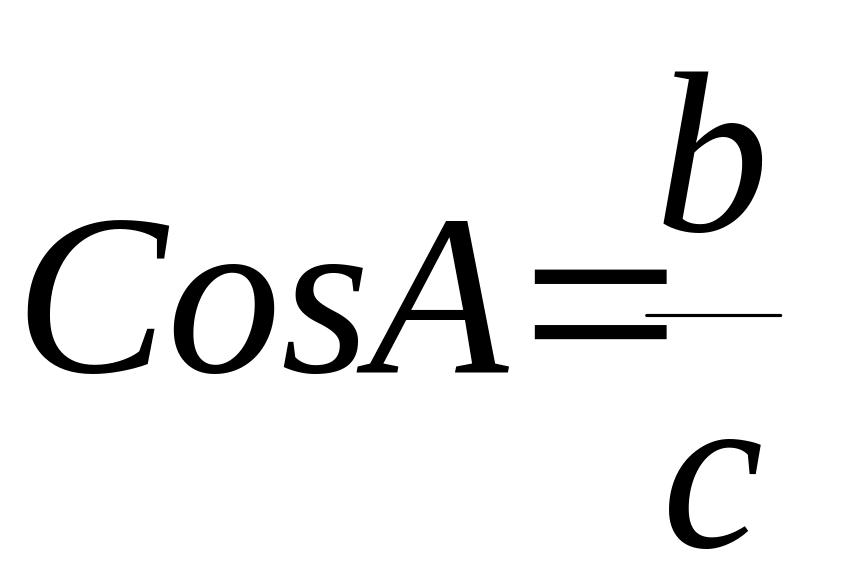 ,
,
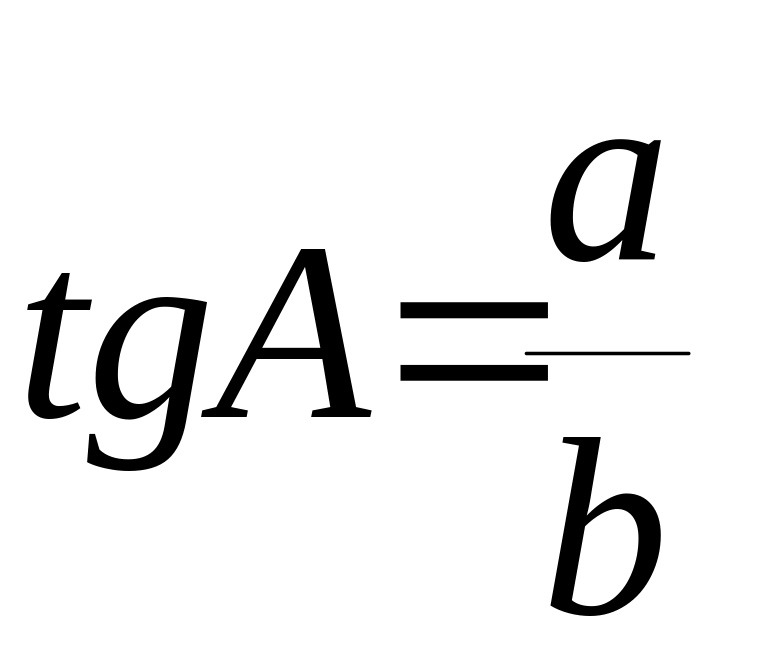 ,
,
b
с
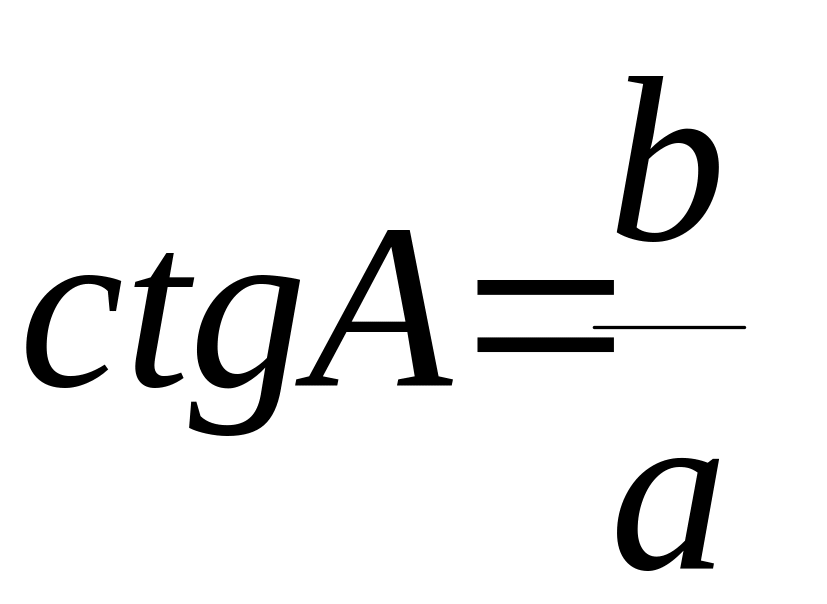
С В
а
12) Площадь треугольника.
а)
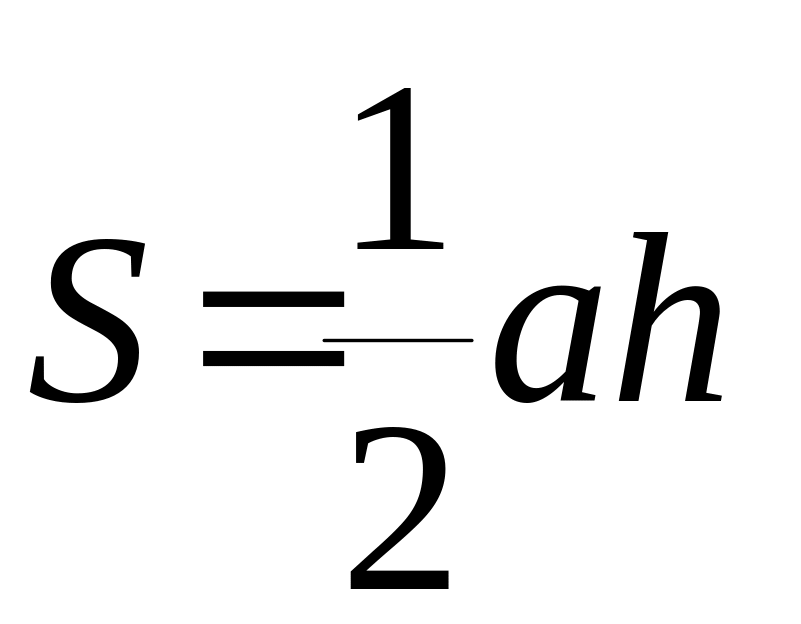 ;
;
б)
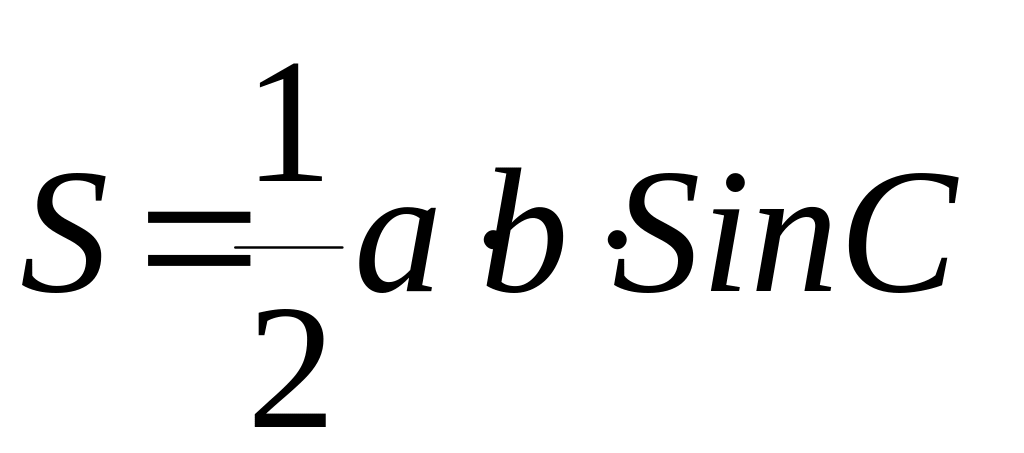 ;
;
в)
![]() ,
где
,
где
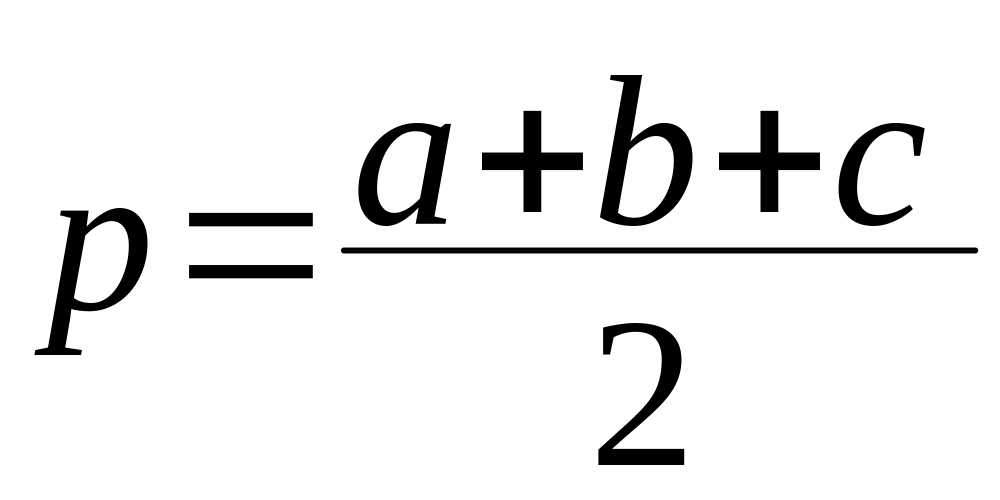 ;
;
г)
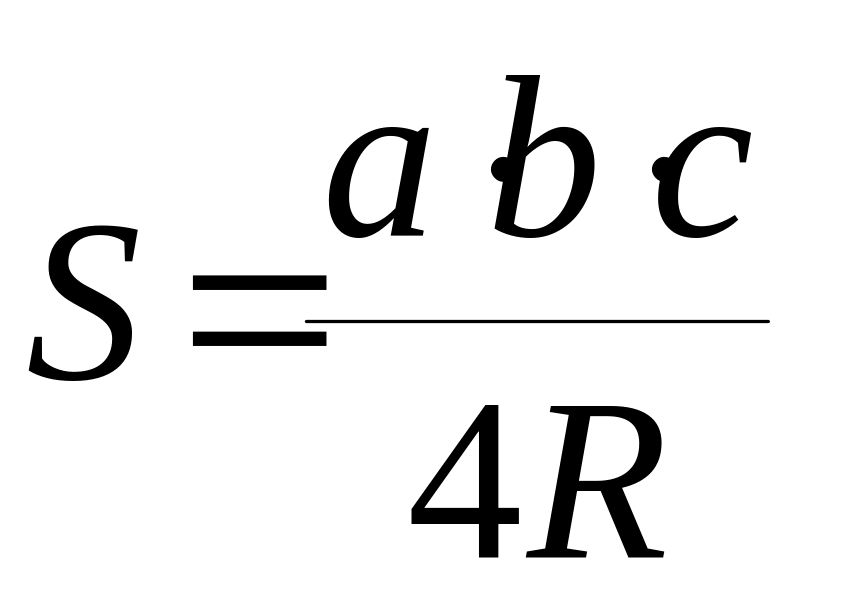 ,
где R
– радиус
описанной окружности;
,
где R
– радиус
описанной окружности;
д)
![]() ;
;
е)
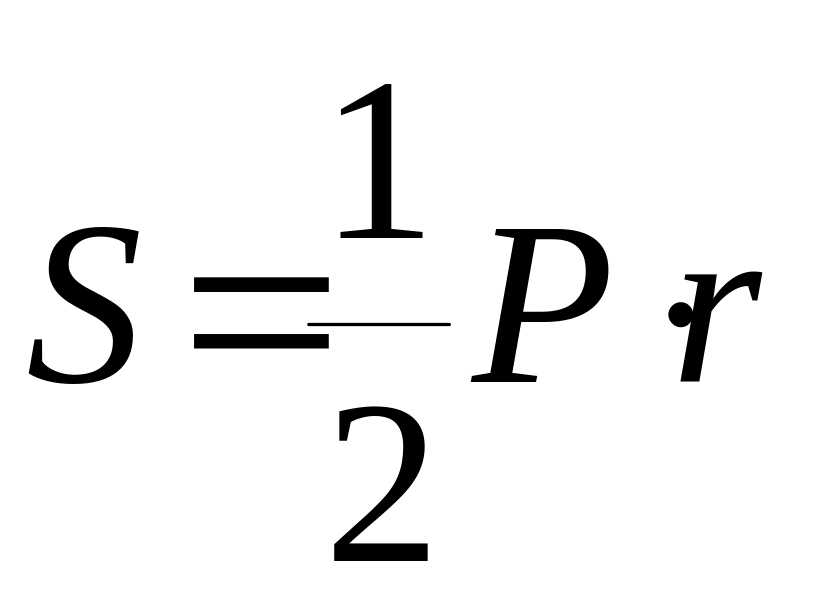 ,
где r
радиус вписанной окружности, Р
– периметр
,
где r
радиус вписанной окружности, Р
– периметр
треугольника;
ж)
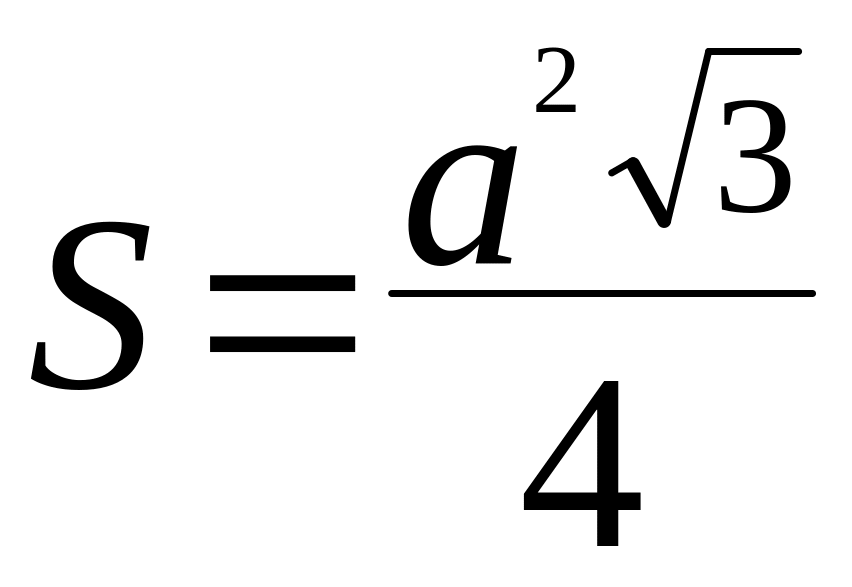 - площадь равностороннего треугольника;
- площадь равностороннего треугольника;
-5-
13) Теорема об отношении площадей треугольников, имеющих равный угол.

 В
В


А С
Площади относятся
как произведение сторон, заключающих
равные углы, то есть если
![]() ,
то
,
то
 .
.
14) Теорема об отношении площадей подобных треугольников.

 В
В


А С
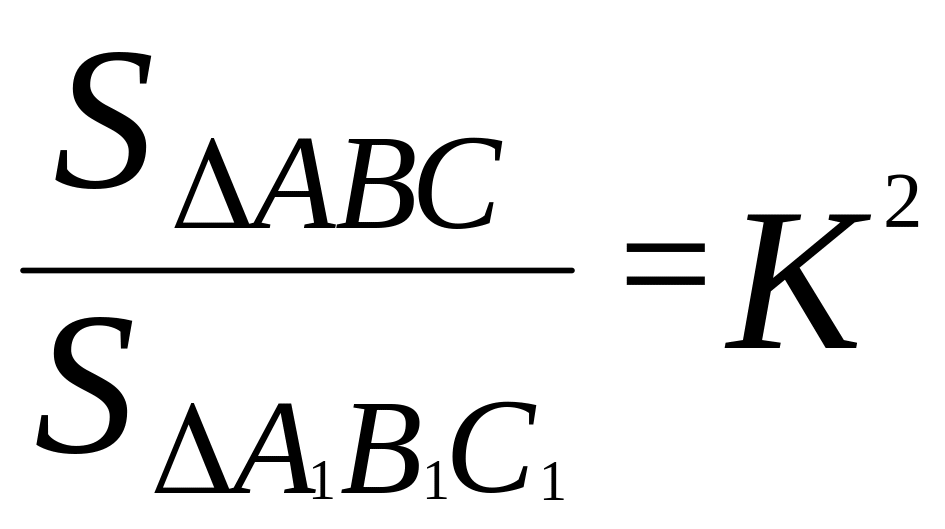 ,
где К
– коэффициент подобия.
,
где К
– коэффициент подобия.
Примечание:
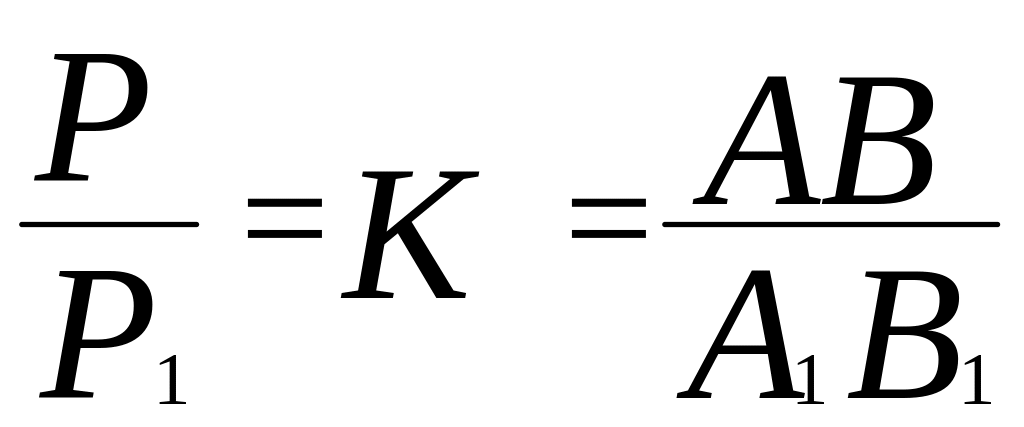
14) Теорема Чевы.
Если три чевианы пересеклись в одной точке, то

В
![]() ,
,![]() ,
,![]() - чевианы.
- чевианы.




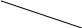

А С
-6-
II. Четырехугольники
1) Параллелограмм.
В а С
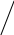



 h
h
![]()
![]() площадь
площадь
b
![]() параллелограмма
АВСD
параллелограмма
АВСD
А D
В С




![]()

A
D
где
![]() и
и
![]() -
диагонали
параллелограмма
АВСD
2) Ромб.
-
диагонали
параллелограмма
АВСD
2) Ромб.
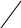

 В
В
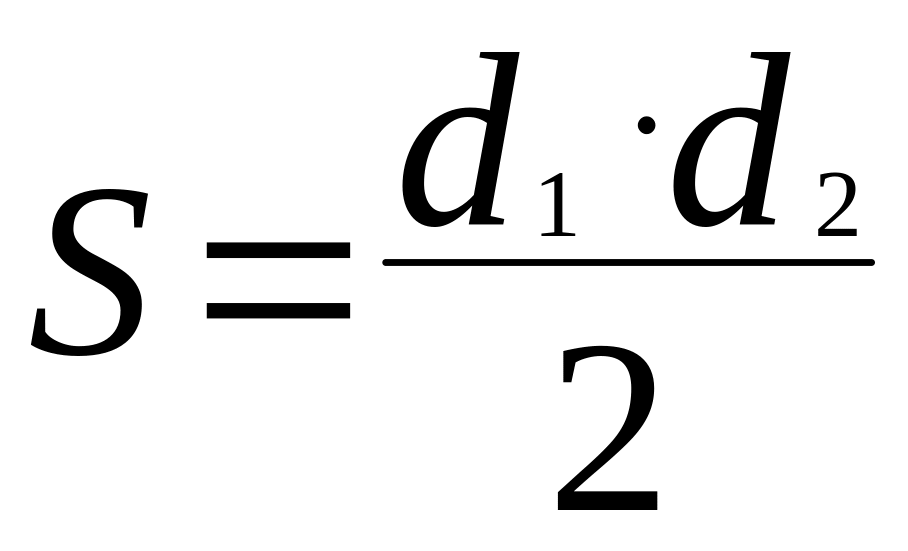 ,
где
и
-
диагонали ромба АВСD
,
где
и
-
диагонали ромба АВСD
 А С
А С
![]() ,
где а
– сторона ромба
,
где а
– сторона ромба
D
3) Трапеция.
 B
b
C
B
b
C 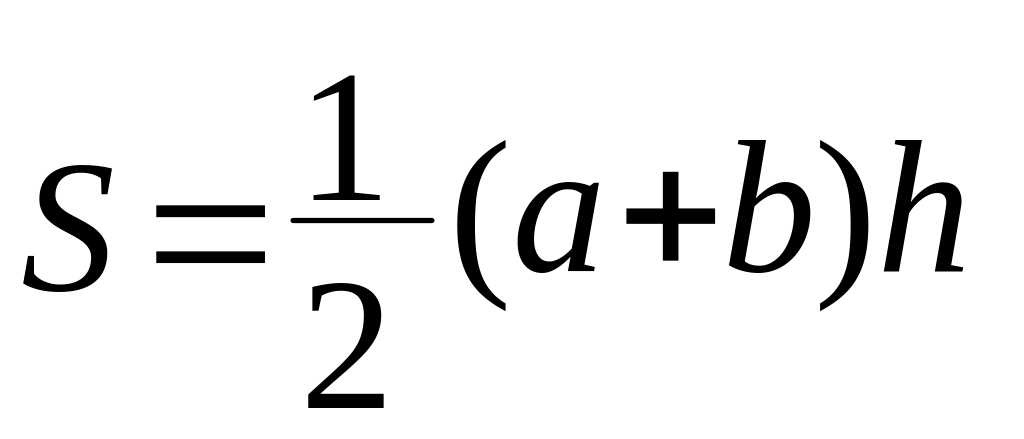
![]() ,
где
,
где
![]() -
средняя линия трапеции
-
средняя линия трапеции
 A
а D
A
а D
4) Свойства описанного четырехугольника.

 b
В
любом описанном четырехугольнике суммы
противо -
b
В
любом описанном четырехугольнике суммы
противо -

 положных
сторон равны:
положных
сторон равны:
a
c
с
![]()

d
5) Свойства вписанного четырехугольника.

 В
любом вписанном четырехугольнике сумма
В
любом вписанном четырехугольнике сумма



 противоположных
углов равна
противоположных
углов равна![]() :
:





![]()




6) Площадь любого четырехугольника, у которого диагонали
перпендикулярны, выражается формулой:
 В
В

 А С
,
где
и
-
диагонали
А С
,
где
и
-
диагонали
D четырехугольника АВСD.
-7-
7) Правильные многоугольники.




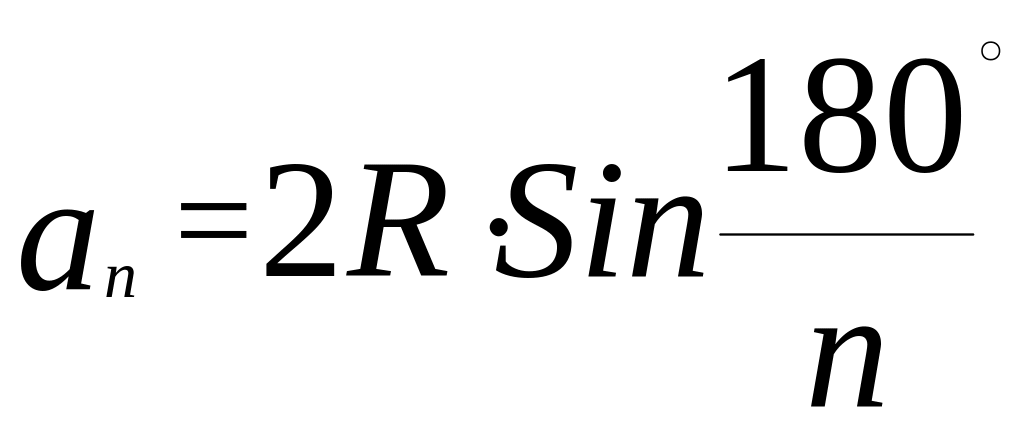 -
сторона
правильного
многоугольника,
-
сторона
правильного
многоугольника,
где R – радиус описанной окружности;
 - сторона правильного
многоугольника,
где – r
радиус
- сторона правильного
многоугольника,
где – r
радиус
вписанной окружности;
I II. Окружность.
1)
 В
В
 АВС
– вписанный,
АВС=
АВС
– вписанный,
АВС=![]() АС;
АС;
С
ADC
–
центральный,
ADC=![]() АС.
АС.
А
2


 )
)
C

 D Углы,
опирающиеся на диаметр прямые.
D Углы,
опирающиеся на диаметр прямые.
B
A

 АВ –
диаметр,
АСВ
=
ADB
=
АВ –
диаметр,
АСВ
=
ADB
=
![]()
3)
D
![]()
A
B
![]()

![]()
