2. Случайные величины

1. Распределения и числовые характеристики одной случайной величины

1. Общие понятия.

Определение. Случайная величина (СВ) – это числовая функция Х(), определенная на множестве элементарных событий   .

Другое определение. Случайная величина – это величина, которая в результате испытания принимает конкретное значение из некоторого множества возможных значений, определяемого условиями испытаний.

Случайные величины обозначают большими буквами латинского алфавита: X, Y, Z, T, а также греческими буквами Различают дискретные и непрерывные случайные величины (ДСВ и НСВ).

Определение. Дискретной случайной величиной называют такую СВ, множество возможных значений которой конечно либо бесконечно, но счётно.

Пример 1. При испытании возможны два элементарных события: успех и неудача. Успеху можно поставить в соответствие значение 1, а неудаче – 0. Тогда мы имеем дело с дискретной СВ X, могущей принимать одно из двух значений: 0 или 1.

Пример 2. В схемах Бернулли и Пуассона число успехов является дискретной СВ, которую можно обозначить через .

Определение. Непрерывной СВ называют такую, множество возможных значений которой представляет собой один или несколько ограниченных или неограниченных интервалов.

Пример. При ежегодных наблюдениях температуры воздуха в определенных месяце, дне и времени суток фиксируют значения температур t₁, t₂,…,t_k,…,t_n (k – номер года) непрерывной случайной величины T. Под элементарным событием понимается равенство T= t_i (i= 1, 2, …,n).

Кроме дискретной и непрерывной СВ может быть дискретно-непрерывная (в дальнейшем такие СВ не рассмотриваются). Например, при розыгрыше лотереи по автобусным билетам обладатель билетов может ничего не выиграть (X=0) или выиграть на общую сумму, которая находится в интервале [ ].

Для того, чтобы характеризовать случайную величину, надо знать не только множество значений, которые она может принять в ходе испытания, но и как часто СВ может их принимать при многократном его повторении.

Определение. Функцией распределения F(x) случайной величины X называется функция, определенная на интервале каждое значение которой есть вероятность события А ≡ ( ), т.е. .

F(x) – полная и универсальная характеристика любой СВ, как НСВ, так и ДСВ. Зная F(x), можно получить любые другие (числовые) характеристики.

Свойства F(x): 1. причем . 2. F(x) – неубывающая, т.е. для . 3. F(x) – непрерывна слева, т.е. при любом x₀ . 4. Вероятность попадания X в полуинтервал: .

Четвёртое свойство получается из очевидного равенства:

2. Распределения дискретной случайной величины (дсв).

В качестве полной характеристики ДСВ применяют либо F(x), либо распределение вероятностей Р(х).

Определение. Распределение вероятностей ДСВ X – это функция

, где (возможно ), , которая принимает ненулевые значения, равные вероятностям событий , только на множестве возможных значений ДСВ Х.

Если заданы то . Функция распределения ДСВ всегда ступенчатая. Если задана F(x), то .

Пример. Пусть Р(х) . Это распределение называется биномиальным. Значения P(x) и F(x) при n=8, p=0,75 указаны в табл.1.

Таблица 1

i	1	2	3	4	5	6	7	8	9	10
	0	1	2	3	4	5	6	7	8	9
P(x)	0,0000	0,0004	0,0038	0,0231	0,0865	0,2076	0,3115	0,2670	0,1001	0
F(x)	0	0,0000	0,0004	0,0042	0,0273	0,1138	0,3214	0,6329	0,8999	1

Графики этих функций имеют вид, изображенный на рис.1 и рис.2.

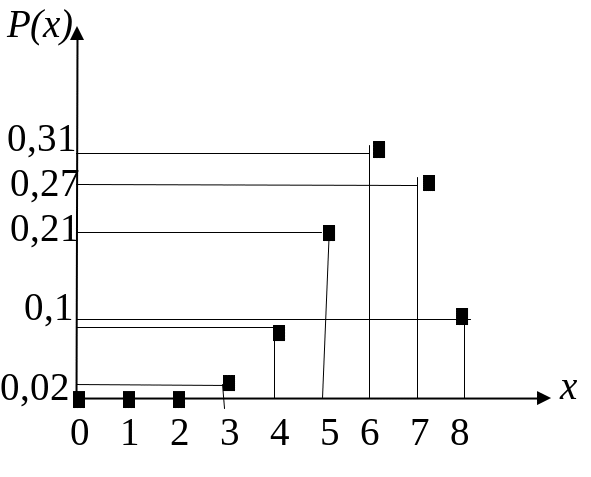
рис.1 рис.2

Примечание. График функции Р(х), представляет собой множество точек с координатами (х_i,P(x_i)), а также точек прямой, совпадающей с осью Ох, с выколотыми точками .