11.1. Задачи

11.1.1. Определить точки пересечения прямой m с поверхностью сферы.

a) б)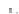

а) б) в)

11.1.2. Определить точки пересечения прямой m с поверхностью цилиндра.

11.1.3. Определить точки пересечения прямой m с поверхностью конуса.

а) б) в)

11.1.4. Определить точки пересечения прямой m с поверхностью тора.

11.1.5. Определить кратчайшее расстояние от точки М до поверхности конуса (а) и от точки А до поверхности цилиндра (б).

а) б)

12. Пересечение поверхностей

12.1. Пересечение кривой поверхности с гранной

Линия пересечения кривой поверхности с многогранником состоит из плоских кривых, каждая из которых получается в результате сечения кривой поверхности одной из граней многогранника. Точки, в которых эти плоские кривые соединяются друг с другом, являются точками пересечения ребер многогранника с кривой поверхностью.

Таким образом, задача на построение линии пересечения кривой поверхности с многогранником может быть сведена к задачам на пересечение кривой поверхности с плоскостью (см. раздел 10) и прямой линией (см. раздел 11).

12.2. Взаимное пересечение кривых поверхностей

Линия пересечения двух поверхностей в общем случае представляет собой пространственную кривую. Эту линию строят по отдельным ее точкам.

Общим способом построения этих точек является метод вспомогательных секущих плоскостей, который заключается в следующем. Пересекая данные поверхности некоторой вспомогательной поверхностью, определяют линии пересечения ее с данными поверхностями. В пересечении этих линий находят точки, принадлежащие искомой линии пересечения.

Наиболее часто в качестве вспомогательных поверхностей применяются плоскости и сферы. Секущие поверхности выбираются таким образом, чтобы они пересекали заданные поверхности по графически простым линиям (прямым или окружностям).

Построение начинают с опорных точек, к которым относятся экстремальные точки (точки, самые близкие и наиболее удаленные от плоскостей проекций) и точки видимости (точки, лежащие на контурной линии поверхности). После этого определяют достаточное число произвольных точек.

12.2.1. Способ вспомогательных секущих проецирующих плоскостей-посредников

Этот способ применяется для построения линии пересечения двух поверхностей в том случае, когда вспомогательные секущие плоскости дают в пересечении с каждой из данных поверхностей такие линии, как прямые или окружности.

Пример. Построить линию пересечения кругового конуса Ф(i,l) со сферой Ф(i’,m) (рис. 12.1).

Для построения линии пересечения в этом случае могут быть использованы в качестве посредников горизонтальные плоскости уровня, которые пересекают и конус и сферу по окружностям. Начинаем с опорных точек. Для определения точек, лежащих на экваторе сферы е (точек видимости) вводим секущую плоскость- посредник , проходящую через экватор сферы. Эта плоскость пересекает сферу по экватору е, а конус- по окружности f радиуса r. Горизонтальные проекции этих окружностей пересекаются в точках А₁ и А’₁, после этого строим фронтальные проекции точек А₂ и А’₂.

Для определения экстремальных точек используется иная секущая плоскость, а именно: параллельная плоскости и являющаяся общей для обеих фигур плоскостью симметрии . Она пересекает сферу по главному меридиану m, а конус- по очерковым образующим l, . В пересечении этих ли­ний на фронтальной проекции определяем точки В₂ и С₂. Затем находим гори­зонтальные проекции точек В₁ и С₁: . Далее определяем нужное число промежуточных точек, находящихся между точками В и С. Вновь применяя при этом секущие плоскости уровня, параллельные плоскости . С помощью плоскости найдены точки D и D’.

Алгоритм нахождения точек D и D’ следующий:

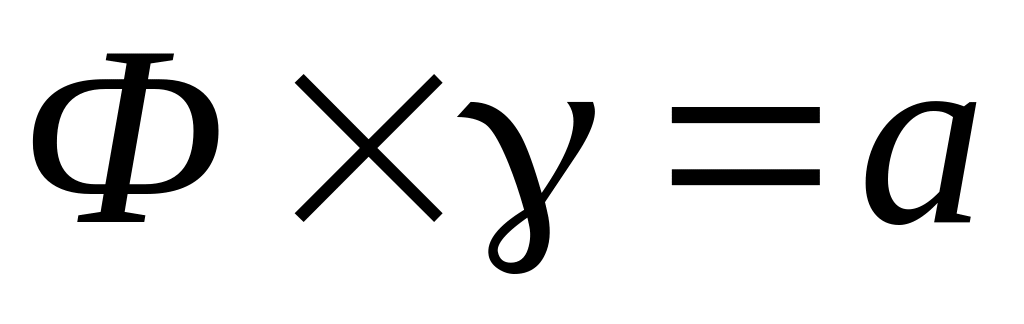1. , где а- окружность радиуса .

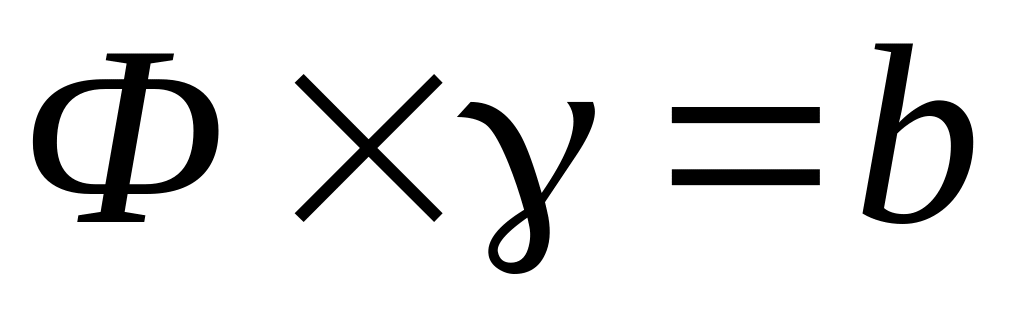2. , где b- окружность радиуса .

Горизонтальные проекции этих окружностей пересекаются в точках D₁ и D’₁, фронтальные проекции находятся на следе проекции . Для определения следующей пары промежуточных точек E и E’ проведена секущая плоскость- посредник . Соединив полученные точки по лекалу, получим проекции линии пересечения поверхностей. Видимость на горизонтальной проекции линии пересечения определяется на двух участках, границами которых служат точки А₁ и А’₁. Участок А₁В₁А’₁ будет видимым, так как промежуточная точка В₁ видимая, следовательно, участок А₁С₁А’₁- невидимый.

Рис. 12.1