Лабораторная работа N11

Изучение сериальннх закономерностей в спектре водорода. Определение постоянной ридберга.

ЦЕЛЬ РАБОТЫ: 1. Градуировка монохроматора по ртутной лампе;

2. Исследование спектров в видимой области (серия

Бальмера);

3. Определение постоянной Ридберга.

ОБОРУДОВАНИЕ: монохроматор УМ-2, ртутная лампа, выпрямитель ВС-4,

индукционная катушка, спектральная трубка водорода.

ЛИТЕРАТУРА: 1. Шпольский Э. С. Атомная Физика . М. 1982.

2. Фриш С. Э. Оптические свойства атомов. Н. Физматгиз.1963.

3. Савельев И. В. Курс обшей Физики т. 3. М. 1980.

4. Кортнев А.В. и др. Практикум по физике. "Высшая школа", 1963.

5. Инструкция - универсальный монохроматор УМ-2.

ТЕОРИЯ

Дискретный характер линейчатого спектра атома водорода и закономер­ности полученные Бальмером и Ритцем находятся в прямом противоречии с классическим истолкованием модели атома Резерфорда. Первая попытка по­строения неклассической теории атома была предпринята в 1913 году Нильсом Бором.

В основе этой теории лежала идея связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома резерфорда, квантовый характер излучения и поглощения света, подтвержденные обширным экспериментальным материалом.

В теории Бора не содержалось принципиального отказа от описания по­ведения электрона в атоме при помощи законов классической физики. Одна­ко Бору пришлось классическое описание дополнить некоторыми ограниче­ниями, накладываемыми на возможные состояния электронов в атоме. Эти ограничения были сформулированы в виде постулатов, физический смысл ко­торых не только не мог быть объяснен в рамках теории, но, более того, противоречил сохраняющемуся в теории классическому описанию движения электрона в атоме, но, тем не менее, они привели к описанию некоторых свойств атомных систем.

Теория Бора применима не только к атому водорода, но и к так назы­ваемой водородоподобной системе, состоящей из ядра с зарядом Ze и од­ного электрона, вращающегося вокруг ядра Не +, Li ++ .

I постулат: существуют некоторые стационарные состояния атома, находясь в которых он не излучает энергию. (Этим состояниям соответствуют определенные орбиты, вращаясь по ко­торым электроны не излучают энергию.)

II постулат: в стационарном состоянии атома, электрон, двигаясь по круговой орбите, должен иметь квантовые значения момента количества движения.

, где n=1, 2, 3… .

III постулат: при переходе атома из одного стационарного состояния в другое испускается или поглощается один квант энергии.

При – выделение кванта.

I и III постулаты связаны с невозможностью обоснования устойчивости ядерной модели атома, а также - со спектральными закономерностями в атоме водорода и квантовой структурой излучения.

Действительно,

,а ,

где целые числа, входящие в формулы серий определяют квантованные зна­чения энергии.

При n_i = 1 – основное энергетическое состояние или невозбужденное. При n_i   W_ = 0, т. е., если электрон удален из атома, то атом ионизирован. Знак " – " показывает, что электрон связан в атоме с ядром силой притяжения.

II постулат явился гениальной догадкой Бора. Он позволяет рассчитать спектр атома водорода.

В теории Бора сохранены основные черты планетарной модели - элек­троны в атомах совершают орбитальное движение вокруг ядра под действи­ем кулоновских сил. Однако орбитами электронов могут быть не все, воз­можные по уравнениям механики, а только стационарные, определяемые ус­ловиями квантования.

Ограничимся рассмотрением круговых стационарных орбит, т.е., примем для атома водорода следующую модель: электрон в атоме водорода равномерно движется по окружности вокруг ядра с зарядом Ze. В этом случае центростремительной силой является кулоновская сила, следовательно, имеет место соотношение F_ц = F_к.

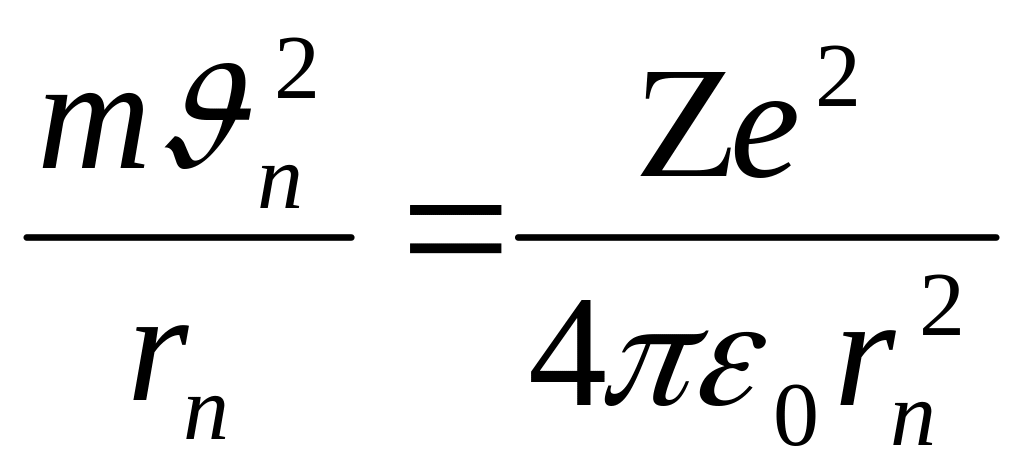(1)

(2)

где е – заряд электрона,

Z – порядковый номер элемента в таблице Менделеева.

r_n – радиус орбиты.

Из всех возможных движений по окружности надо выбрать такие, которые удовлетворяют условию квантования

(3)

Из (2) и (3) можно определить неизвестные _n и r_n

откуда

(4)

Чем меньше "n" (ближе орбита к ядру), тем больше скорость враще­ния электрона.

Подставив (4) в (3), получим:

откуда

(5)

т.е., радиусы стационарных орбит относятся как целые числа 1:4:9:16:25 ....

Полученные соотношения недоступны экспериментальной проверке. Для проверки теории надо вычислить такие величины, которые можно проверить на опыте. Такой величиной является энергия, излучаемая и поглощаемая ато­мами.

Найдем полную энергию электрона, находящегося в стационарном состоянии.

W_полн.= W_к+W_п

Поле создается положительным ядром и на расстоянии r_n от него, где находится электрон, потенциал будет:

Потенциальная энергия электрона в атоме будет отрицательной.

Кинетическая энергия электрона на орбите "n" будет равна

(6)

Тогда полная энергия электрона на орбите "n" будет:

(7)

Подставляя (5) в (7), получим:

(8)

Отрицательное значение полной энергии электрона в атоме означает, что при удалении электрона из атома не происходит выделения энергии (совершения работы), а наоборот, необходима затрата энергии извне, равная W_полн., если считать, что удаленный электрон будет иметь нуле­вую полную энергию.

Из (8) следует, что электрон в поле ядра может обладать только некоторыми дискретными значениями полной энергии, так как " n " может принимать значения 1, 2, 3,..., но не дробные.

Квант лучистой энергии, излученный при переходе электрона из одного стационарного состояния в другое будет равен

Введем волновое число , учитывая что

(9)

Обозначим множитель через R (постоянная Ридберга).

(10)

Численное значение постоянной Ридберга, полученное из выражения (10) равно R_теор. = 109737,303 см ^-1, а экспериментальное R_эксп. = 1О9677, 581 см ^-1 такое расхождение определяется несколькими причинами, одна из них состоит в том, что при выводе формулы (8) ядро атома считалось не­подвижным. В действительности ядро имеет конечную массу, поэтому дви­жение электрона и ядра происходит вокруг общего центра тяжести. Тогда энергия электрона в атоме и постоянная R будут зависеть от массы ядра и запишутся в виде:

(11)

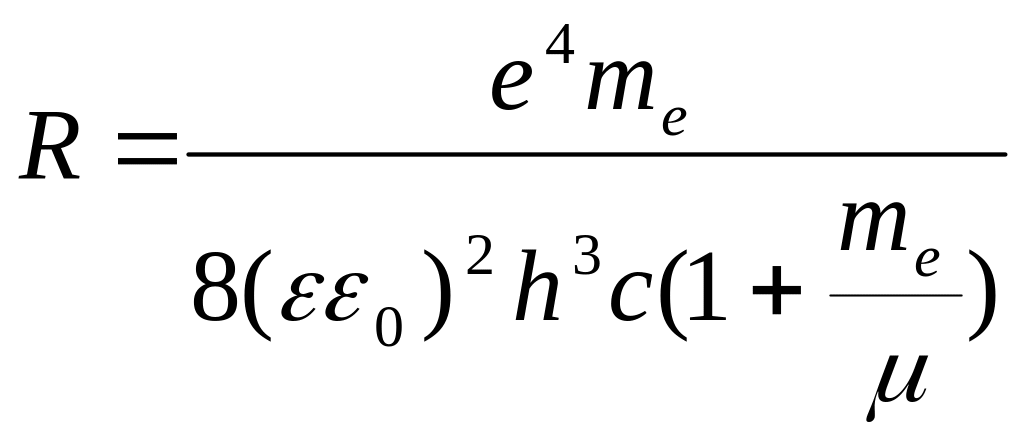(12)

Соотношение (9) показывает, что волновые числа выражаются разностью двух слагаемых - термов, следовательно, теория Бора правильно устанав­ливает характер излучения водородоподобных атомов.

Теория Бора сделала ясным физический смысл спектральных серий. Спек­тральные серии представляют собой монохроматические излучения, которые возникают в результате перехода атома в стационарное состояние из всех воз­можных возбужденных состояний, расположенных выше данного. Так, серия Лаймана соответствует переходам из возбужденных состояний в нормаль­ное, характеризуемое значением квантового числа n = 1. Волновые чис­ла серии Лаймана выражаются соотношением:

(13)

Серия Бальмера образуется в результате перехода на уровень n = 2:

(14)

Идеи Бора оказались чрезвычайно плодотворными:

1. Теория Бора позволила выяснить физический смысл спектральных серий.

2. Все линии одной серии имеют границу со стороны коротких волн (n=). Эта граница и является пределом, к которому стремятся, сгущаясь линии, принадлежащие данной серии.

3. Все линии известные из опытных данных имеют длины волн, совпадающие с расчетными до шестого знака, что служит лучшей проверкой рассматри­ваемой теории спектров и оправданием постулатов.

4. Радиус орбиты, вычисленный по формуле (4) при n = 1 r=5,410^-11м совпадает с радиусом орбиты электрона подсчитанным другим способом.

5. Теория Бора объясняет правильно не только спектр испускания водорода, но такие и спектр поглощения. Установлено, что спектры поглощения газообразных веществ имеют та­кой же линейчатый характер, как и спектры испускания. В спектре погло­щения имеются те же линии, что и в спектре испускания. Однако, в то время, как в спектре излучения имеются серии Лаймана, Бальмера, Пашена и другие, в спектре поглощения атомарного водорода имеется только одна серия Лаймана. Лишь только в том случае, когда водородные атомы оказы­ваются возбужденными, в спектре поглощения водорода обнаруживаются ли­нии, принадлежащие серии Бальмера. По теории Бора так и должно быть, ибо нормально свободные атомы водорода находятся в стационарном состоянии с наименьшей энергией (n=1) и могут, следовательно, поглощать кванты только такой энергии, резуль­татом поглощения которой явится переход электронов на более высокие уровни.

6. Теория Бора позволяет вычислить величину работы, которую необходимо совершить для удаления электрона из атома водорода, т.е. Для образова­ния водородного иона. В нормальном состоянии электрон находится в ста­ционарном состоянии с энергией W₁= -13,5 эВ. За пределами атома водо­рода электрон свободен, потенциальная энергия его равна нулю и полная энергия электрона определяется только величиной его кинетической энер­гии. Наименьшее возможное значение кинетической энергии свободного электрона равно нулю. Поэтому за пределами атома водорода наименьшее значение энергии электрона будет также равно нулю. Очевидно, чтобы пе­ревести электрон из основного стационарного состояния в свободное, на­до затратить энергию W_полн. = 13,5 эВ. Соответствующие измерения подтвердили, что для образования иона водоро­да действительно необходимо затратить энергию, равную 13,5 эВ.

7. Бору удалось качественно объяснить закономерности расположения эле­ментов в периодической системе Менделеева на основе представления о слоях и оболочках, в которые группируются "разреженные" состояния эле­ктронов и которые заполняются по мере увеличения числа электронов в атоме.

8. Теория Бора была весьма крупным шагом в развитии теории атома. Она с полной отчетливостью показала неприменимость классической физики к внутриатомным явлениям и главенствующее значение квантовых законов в микромире.

9. После первых успехов теории все яснее давали себя знать ее недочеты. Все попытки построения теории атома гелия окончились неудачей.

10. Гипотеза о том, что в стационарном состоянии движение электрона происходит по одной из орбит, не была обоснована.

11. Слабой стороной теории Бора была ее внутренняя противоречивость: она не была ни последовательно классической (квантование), ни последо­вательно квантовой теорией (понятие траектории).

12. Эта теория не может объяснить спектры излучения более сложных ато­мов и различную интенсивность спектральных линий. Эти трудности были преодолены квантовой теорией, показавшей неприменимость классических представлений к микрообъектам.

13. Несмотря на перечисленные недостатки, боровская теория явилась од­ним из важнейших этапов в создании современной квантовой механики, уста­новившей закономерности поведения частиц малой массы и объяснившей все особенности строения и свойств атомов, молекул и твердых тел. В то же время квантовая механика, принимающая во внимание волновые свойства электрона, объяснила первые успехи боровской теории и установила пре­делы ее применимости. Оказалось, что в состоянии большего возбуждения атома (большие n), (когд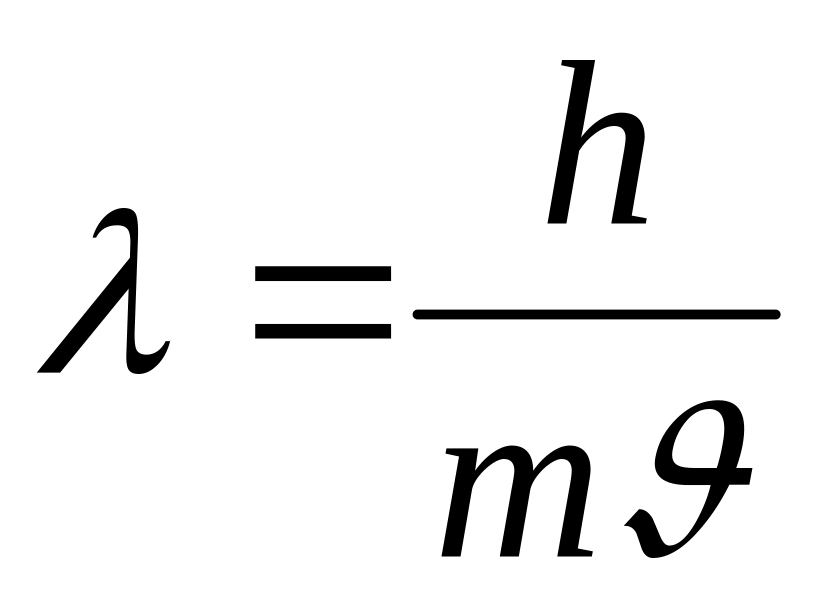а мала по сравнению с линейными размерами, определяющими область движения электрона) можно приближенно говорить о траектории электрона.