Определение радиусов начальных окружностей и межосевого расстояния
Изобразим схему эвольвентного зацепления упрощенно (рис. 4).
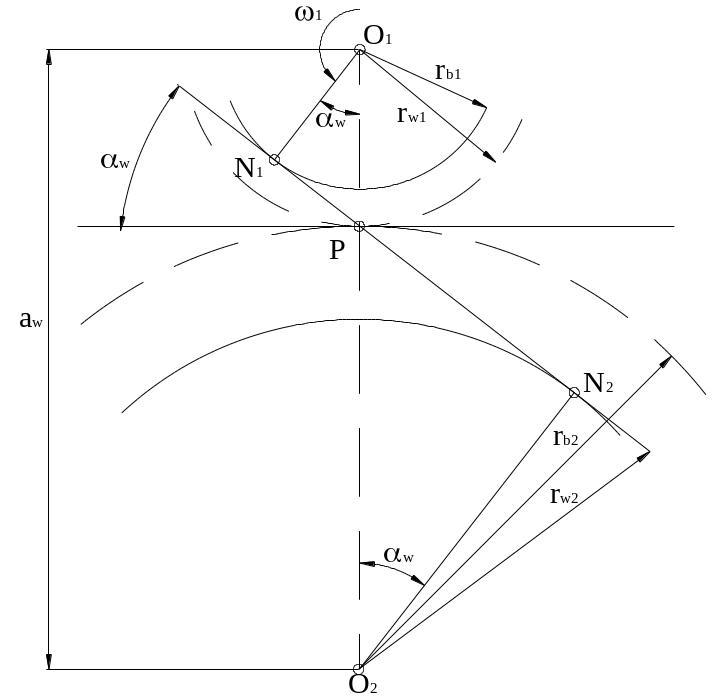
Рисунок 4 – Определение радиусов начальных окружностей и межосевого расстояния
Оси вращения двух эвольвентных зубчатых колес О1 и О2 соединим межосевой линией. На межосевой линии О1О2 выберем полюс зацепления Р и проведем начальные окружности радиусами rw1 и rw2. Под углом w к горизонтали, проходящей через полюс зацепления, проведем линию зацепления. Из центров О1 и О2 опустим перпендикуляры на линию зацепления. Точки пересечения обозначим N1 и N2 соответственно.
Из условия нарезания эвольвентных колес мы знаем, что отрезки O1N1 и O2N2 являются радиусами соответствующих основных окружностей зубчатых эвольвентных колес rb1 и rb2.
Из O1N1P1 определяем радиус основной окружности
.
При рассмотрении нарезания зубчатых колес нами получена зависимость
.
Приравняем правые части этих уравнений
.
Откуда
.
[2]
Это второе уравнение плотного зацепления.
Проанализируем это уравнение.
Когда
,
,
тогда
,
т.е. при нулевом и равносмещенном зацеплениях радиусы начальных и делительных окружностей совпадают.
Когда
,
,
.
В неравносмещенном зацеплении радиусы начальных и делительных окружностей не совпадают.
При
,
,
,
,
следовательно
.
При положительной угловой коррекции радиусы начальных окружностей увеличиваются по сравнению с нулевым зацеплением.
Определим межосевое расстояние.
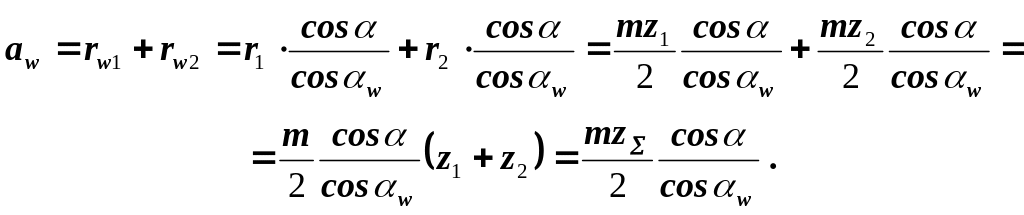
При х
= 0,
,
.
При х
> 0,
,
.
При положительной угловой коррекции межосевое расстояние увеличивается по сравнению с нулевым зацеплением.
Выражение
принято
обозначать (1+0),
где 0
– коэффициент изменения межосевого
расстояния. Тогда
.
Рассмотрим эти 2 уравнения плотного зацепления.
зависит
от х0,
w
х0
– однозначная зависимость;
,
w
0
– тоже однозначная зависимость.
Это позволило составить таблицы, по которым по значению суммарного относительного коэффициента смещения х0 определяют угол зацепления w и коэффициент изменения межосевого расстояния 0.
Затем радиусы начальных окружностей и межосевое расстояние определяются по формулам:
Определение высоты зуба
Изобразим окружности впадин двух эвольвентных зубчатых колес с центрами вращения О1О2 (рис.5). Расстояние между окружностями впадин обозначим . Как видно из рисунка, это расстояние равно межосевому расстоянию аw за вычетом радиусов окружностей впадин rf1 и rf2:
.
На этом расстоянии должна поместится высота зуба h и радиальный зазор с.
Высота зуба определяется двумя способами.
Рисунок 5 – Определение высоты зуба
1й способ основан на том, что в зацеплении должен сохраняться стандартный зазор
,
тогда
.
2й способ заключается в том, что должно быть сохранено отношение высоты зуба к расстоянию в некорригированном и корригированном зацеплениях.
.
Определим
в
некорригированном зацеплении исходя
из стандартных размеров инструментальной
рейки.
.
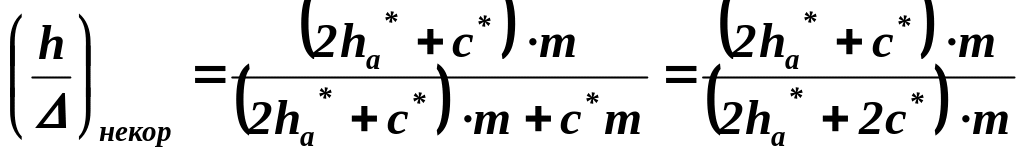Подставим стандартные размеры для нормального зуба рейки:
.
Следовательно, для некоригированных колес соблюдается зависимость
.
Аналогично для корригированных колес
.
При этом зазор получается немного меньше стандартного, зато немного увеличивается коэффициент перекрытия.