Равносмещенное зацепление (зацепление с высотной коррекцией)
Рисунок 3 – Основные размеры колес и параметры равносмещенного зацепления
Равносмещенным называется такое зацепление, суммарное смещение в котором равно нулю. При этом при нарезании колеса с меньшим числом зубьев принимается положительное смещение, с большим числом зубьев – отрицательное смещение.
;
;
;
.
Изобразим
нарезание большего зубчатого колеса
эвольвентой рейкой с отрицательным
смещением
.
При этом начальные окружности колес будут касаться делительной линии инструмента в точке Р, а линия зацепления пройдет через полюс зацепления Р и точки контакта зубьев колес.
Определим основные геометрические размеры зацепления по рис.3.
Высота головки зуба
,
.
и меньшого колеса с таким же положительным смещением (рис.3).
Высота ножки зуба
,
.
Радиусы окружностей выступов
,
.
Радиусы окружностей впадин
,
.
Радиусы начальных окружностей
,
.
Толщины зубьев по начальной окружности
,
.
Ширина впадин на начальной окружности
,
.
Угол зацепления
.
Межосевое расстояние
.
Неравносмещенное зацепление (с угловой коррекцией). Уравнение плотного зацепления
Рассмотрим случай, когда смещение средней линии инструментальной рейки положительно при нарезании зубчатых колес с меньшим и большим числом зубьев: x1>0; x2>0; x>0.
Шаг по начальной окружности для любого колеса равен сумме ширины впадины и толщины зуба по начальной окружности.
.
Зацепление плотное, если толщина зуба по начальной окружности одного колеса равна ширине впадины по начальной окружности другого колеса.
,
,
,
,
.
Условие плотного зацепления запишем в виде
.
[1]
Шаг на начальной окружности равен сумме толщин зубьев колес по начальным окружностям.
Найдем шаг по начальной окружности через длину начальной окружности и количество зубьев первого колеса
.
Толщины зубьев колес по начальным окружностям найдем по известной формуле толщины зуба по дуге любой окружности
,
.
Подставим полученные значение в формулу [1]
Сократим
на 2 и раскроем скобки
Перемножим
левую и правую части уравнения на
выражение
.
– отношение
радиусов начальных окружностей зубчатых
колес прямопропорционально отношению
чисел их зубьев.
Сократим на и сгруппируем подобные члены уравнения
Из полученного уравнения определим invw, разделив левую и правую части на (z1+z2).
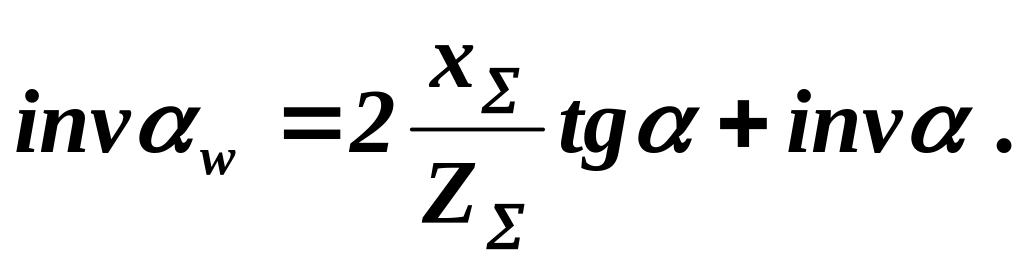[1]
Это и есть основное уравнение плотного зацепления. Этим уравнением можно пользоваться для определения параметров зацепления с любой коррекцией.
Для нулевого зацепления
;
;
;
.
Для равносмещенного зацепления
; ; .
Для неравносмещенного зацепления
;
;
.
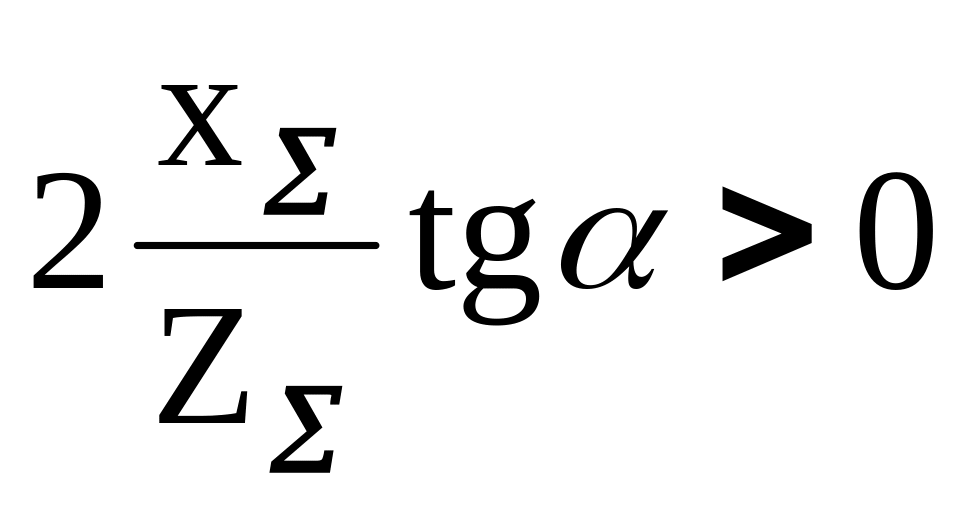Поэтому зацепление называется с угловой коррекцией.
При положительной угловой коррекции угол зацепления увеличивается.
В
анализируемом выражении [1] inv
и tg
– величины постоянные. Следовательно
invw
зависит только от
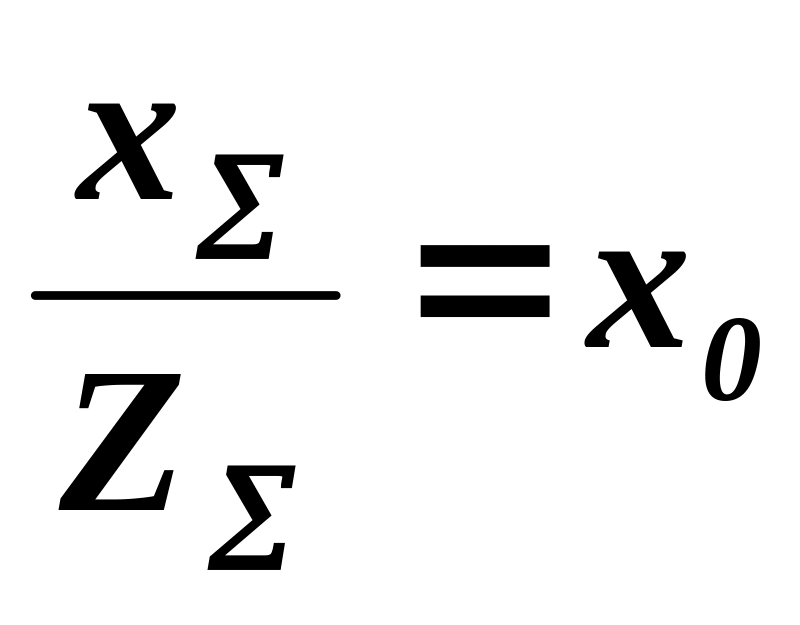– коэффициента относительного смещения,
.