Проверка зубьев на незаострение

Если в формулу определения толщины зуба по дуге любой окружности подставить вместо радиуса r_y радиус окружности вершин r_a, получим толщину зуба колеса по окружности вершин

Правильно спроектированное зубчатое колесо должно иметь незаостренный зуб, то есть эвольвенты правого и левого профилей зуба колеса должны по окружности вершин быть на некотором расстоянии друг от друга и не пересекаться в пределах высоты зуба.

Рекомендуется принимать:

если зубья колеса не подвергаются термообработке;

если зубья колеса подвергаются термообработке.

Контролируемые размеры эвольвентных зубчатых колес

В процессе нарезания зубчатого эвольвентного колеса возникает необходимость в контроле его размеров. Диаметр заготовки, как правило, известен. При нарезании зубьев необходимо контролировать 2 размера: толщину зуба и шаг зубьев. Существует 2 контролируемых размера, косвенно определяющих эти параметры:

1. толщина зуба по постоянной хорде (измеряется зубомером),

2. длина общей нормали (измеряется скобой).

Толщина зуба по постоянной хорде

Представим себе, что мы нарезали эвольвентное зубчатое колесо, а затем рейку ввели с ним в зацепление (одели на него рейку). Точки касания рейки с зубом окажутся расположенными симметрично с двух сторон зуба. Расстояние между точками касания и есть толщина зуба по постоянной хорде.

Изобразим зуб эвольвентного колеса. Для этого проведем вертикальную ось симметрии (рис.4) и с центром в точке O проведем радиус окружности выступов r_a и радиус делительной окружности r. Расположим зуб колеса и впадину рейки симметрично относительно полюса станочного зацепления P_c, который находится на пересечении вертикальной оси симметрии и делительной окружности. Через полюс станочного зацепления P_c проходит делительная линия рейки. Угол между делительной линией и касательной к основной окружности является углом зацепления в процессе нарезания, который равен профильному углу рейки .

Обозначим точки касания рейки с зубом колеса А и В, а точку пересечения линии, соединяющей эти точки, с вертикальной осью – D.

Отрезок AB и есть постоянная хорда. Обозначается постоянная хорда индексом . Определим величину толщины зуба колеса по постоянной хорде. Из рис.4 видно, что

Из треугольника ADP_c определим

Обозначим отрезок EC на делительной линии – ширину впадины рейки по делительной линии, которая равна дуговой толщине зуба колеса по делительной окружности

Отрезок AP_c перпендикулярен профилю рейки и является касательным к основной окружности колеса. Определим отрезок AP_c из прямоугольного треугольника EAP_c

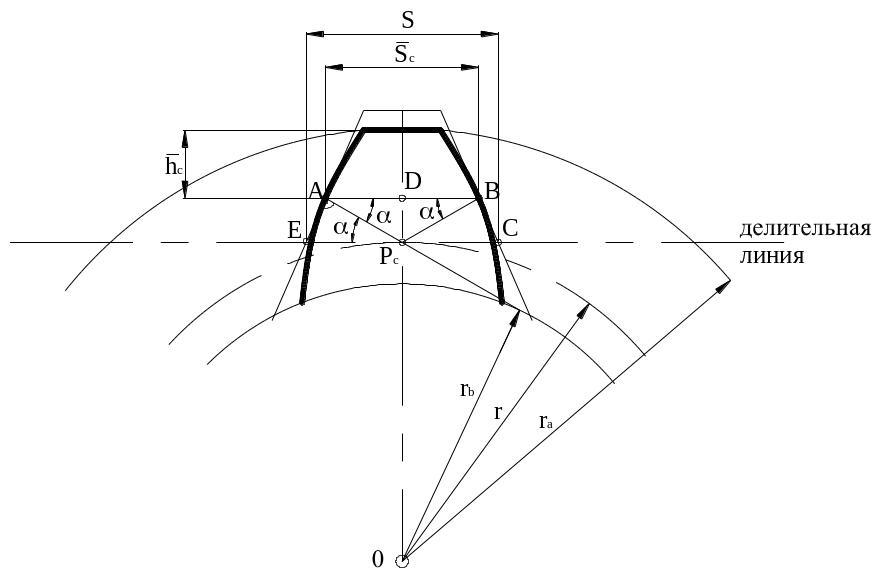
Рисунок 4 – Толщина зуба по постоянной хорде

Подставим полученное выражение в предыдущую формулу

Но отрезок , следовательно

Таким образом толщина зуба по постоянной хорде

Как видно из полученной формулы толщина зуба по постоянной хорде не зависит от количества нарезаемых зубьев колеса z, поэтому она и называется постоянной.

Для того, чтобы можно было контролировать толщину зуба по постоянной хорде зубомером, нам нужно определить еще один размер – расстояние от окружности выступов до постоянной хорды. Этот размер называется высотой зуба до постоянной хорды и обозначается индексом (pис.4).

Как видно из рис.4

Из прямоугольного треугольника определяем

Но , следовательно

Таким образом получаем высоту зуба эвольвентного колеса до постоянной хорды

Полученные размеры дают возможность контролировать размеры зуба эвольвентного колеса в процессе нарезания.