6. Связь между параметрами эвольвентных колес и параметрами зацепления

Мы установили, что N₁O₁P и N₂O₂P подобны. Из подобия треугольников следует, что N₁O₁P=N₂O₂P . Стороны угла зацепления _w перпендикулярны сторонам этих углов. Следовательно

Центральные углы между межосевой линией и радиусами, проведенными в точки касания общей нормали с основными окружностями равны между собой и равны углу зацепления.

Из рассмотренных треугольников определим радиусы основных окружностей r_b1 и r_b2 через угол зацепления _w и радиусы начальных окружностей r_w1 и r_w2.

Здесь r_b – параметр колеса, r_w , _w - параметры зацепления.

Параметры зацепления:

1. Межосевое расстояние – а_w.

2. Радиусы начальных окружностей – r_w1 и r_w2.

3. Угол зацепления – _w.

4. Линия зацепления – N₁N₂.

Эвольвентное реечное зацепление

Эвольвентное реечное зацепление представляет собой зацепление эвольвентного колеса с эвольвентной рейкой и предназначено для преобразования вращательного движения зубчатого колеса в поступательное движение рейки и наоборот.

Выясним, какой профиль имеет зуб эвольвентной рейки, находящейся в зацеплении с эвольвентным колесом. Пусть мы имеем два эвольвентных колеса, у одного из которых число зубьев равно бесконечности (z =), т.е. мы выпрямили в одну линию зубья колеса. Это и будет эвольвентная рейка.

Изобразим зацепление двух эвольвентных колес с центрами O₁ и O₂ и радиусами основных окружностей r_b1 и r_b2. Проведем межосевую линию O₁O₂ и общую касательную к основным окружностям N₁N₂ (рис. 2). На пресечении O₁O₂ и N₁N₂ получим точку Р – полюс зацепления. Через Р проведем линию, перпендикулярную O₁O₂.

Пусть эвольвента первого колеса Э₁ зацепляется с эвольвентой второго колеса Э₂ в полюсе Р. Тогда радиус кривизны эвольвенты Э₁ в точке Р равен отрезку нормали N₁P, а радиус кривизны эвольвенты Э₂ в точке Р равен отрезку нормали N₂P:

_Э1=N₁P, _Э2=N₂P.

Предположим, что число зубьев первого колеса не изменяется (z₁=const). Увеличим число зубьев второго колеса. При этом увеличится межосевое расстояние a_w. Точка О₂ займет новое положение – O₂’.

. Увеличится радиус основной окружности r_b2. Увеличится отрезок PN₂, так как точка N₂ займет новое положение N₂’. Следовательно увеличится радиус кривизны эвольвенты Э₂ в точке Р.

Угол зацепления _w не меняется, поскольку z₁=const. В пределе центр второго колеса окажется в бесконечности при увеличении z₂ →  . Тогда и радиус кривизны эвольвенты Э₂ _Э2=. Эвольвента Э₂ превратится в прямую линию, перпендикулярную N₁N₂. Эта прямая и есть предельная эвольвента.

Профиль зуба эвольвентной рейки является прямой линией, перпендикулярной линии зацепления, а сечение зуба - трапеция (вторая ветвь эвольвенты тоже превращается в прямую линию).

В эвольвентном реечном зацеплении вместо постоянства угловых скоростей колес имеется постоянство отношения угловой скорости колеса к линейной скорости рейки. Начальная окружность колеса 2 превратилась в начальную прямую, катящуюся без скольжения по начальной окружности колеса 1. Угол между профилем и перпендикуляром к начальной прямой - угол профиля - равен углу зацепления (по взаимной перпендикулярности сторон).

Точка касания начальной окружности с начальной прямой (полюс зацепления) является мгновенным центром вращения колеса 1 в относительном движении.

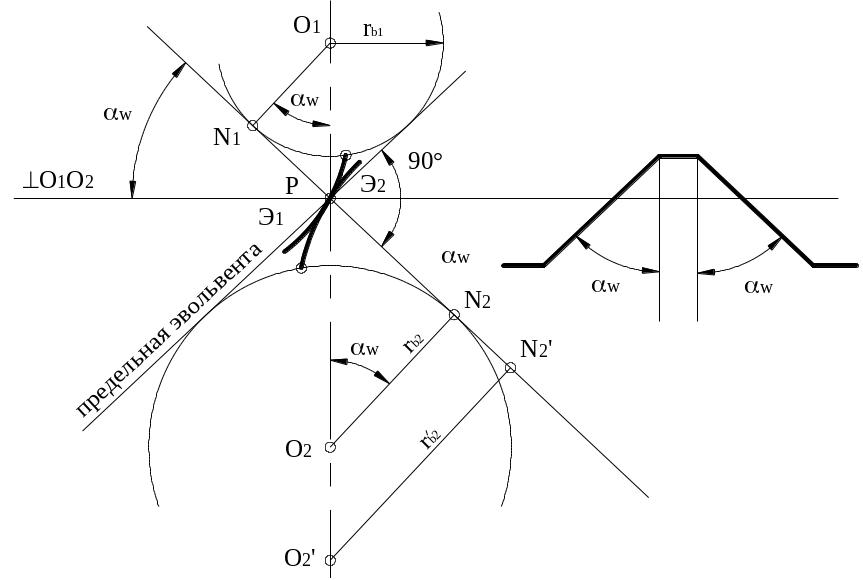
Рисунок 2 – Образование профиля эвольвентной рейки

Если отношение скорости эвольвентной рейки к угловой скорости зацепляющегося с ней колеса величина постоянная, то колесо эвольвентное. Линия зацепления при этом прямая, проходящая через полюс зацепления по касательной к основной окружности, перпендикулярно к профилю зуба.

Форма профиля зуба эвольвентной рейки сыграла исключительно большую роль в широком распространении эвольвентного зацепления.