6. Тело совершает плоско-параллельное движение (рис.7).

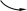S

Рисунок 7- Плоско-параллельное движение тела

Плоско-параллельное движение тела раскладываем на поступательное вместе с центром масс S и вращение вокруг центральной оси, проходящей через центр масс S.

Тогда: для поступательного движения вместе с центром масс S (полюсом) получим главный вектор сил инерции:

.

Для вращательного движения вокруг полюса – центра масс S получим главный момент сил инерции:

.

Геометрически сложив главный вектор сил инерции и главный момент сил инерции получим равнодействующую силу , смещённую от центра масс на плечо так, что момент этой силы совпадает с главным моментом сил инерции материального тела.

Способ проф. Н.Е.Жуковского (теорема о жёстком рычаге)

В силовом анализе механизмов часто встречаются задачи, когда нет необходимости определять силы реакций в кинематических парах, а необходимо лишь определить уравновешивающую силу или уравновешивающий момент при заданных силах полезного сопротивления. При этом удобно пользоваться методом Жуковского.

Теорема Жуковского доказывается из принципа возможных перемещений.

Возможное перемещение это:

1. бесконечно малое;

2. воображаемое;

3. не вызывающее разрушения связей.

Способ Жуковского заключается в следующем:

если на план скоростей, повёрнутый на 90 в любую сторону, приложить в соответствующие точки все внешние силы, действующие на механизм, в том числе и силы инерции звеньев, то сумма моментов всех сил с учётом уравновешивающей силы относительно полюса плана скоростей механизма в заданном положении равна нулю, т.е. план скоростей рассматривается как некоторый жёсткий рычаг с шарнирным закреплением в полюсе плана скоростей. Докажем это.

Из курса теоретической механики известно, что принцип возможных перемещений заключается в следующем:

Для равновесия механической системы необходимо и достаточно, чтобы сумма элементарных работ всех действующих на неё активных сил на возможном перемещении системы была равна нулю.

или

. [1]

Если система тел под действием заданных сил не находится в равновесии, то необходимо добавить силы инерции и получить систему сил, отвечающую условиям равновесия.

В уравнении [1]:

- силы, приложенные к системе, в том числе и силы инерции;

- возможное перемещение точек приложения сил;

- угол между вектором силы и вектором возможного перемещения точки приложения силы.

Разделим обе части уравнения [1] на dt:

Здесь - возможная скорость точки приложения силы .Tогда - угол между вектором силы и вектором возможной скорости точки приложения силы.

Из уравнения элементарных работ [1] мы получим уравнение мощностей [2].

[2]

Величину скорости любой точки механизма удобно определять построением плана скоростей.

Построим план скоростей некоторой точки i механизма, движущейся по своей траектории со скорсьтю под действием некоторой силы (рис 8а). - угол между направлением силы и скоростью точки i. Сила будет направлена по вектору ускорения точки .План скоростей точки i изобразим повёрнутым на 90 по часовой стрелке (хотя этот поворот может быть выполнен и против часовой стрелки). Изображение . При этом [3]. Заданную силу из схемы механизма переносим в соответствующую точку i на план скоростей (рис 8б) и из полюса плана скоростей на направление силы опустим перпендикуляр . Угол между лучами и равен углу между Vi и , так как их стороны взаимно перпендикулярны.

1. б

   

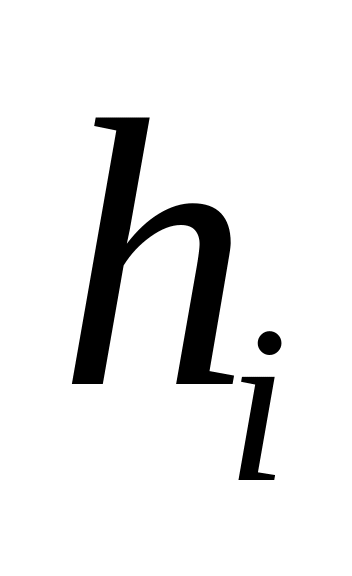
   i

   

   

   

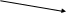
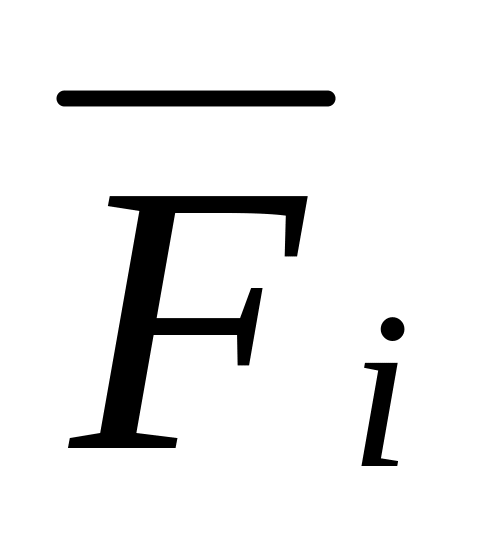
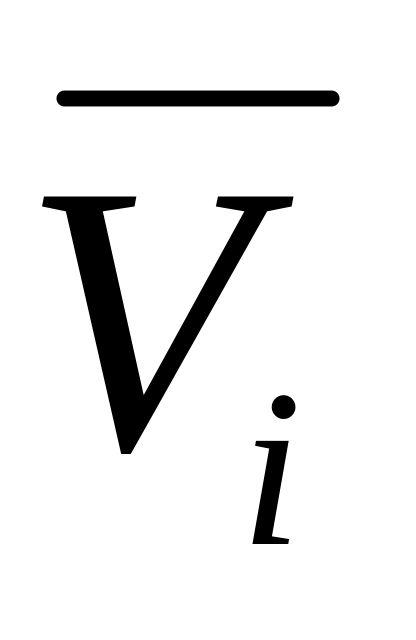
   i

   

   

   )

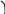
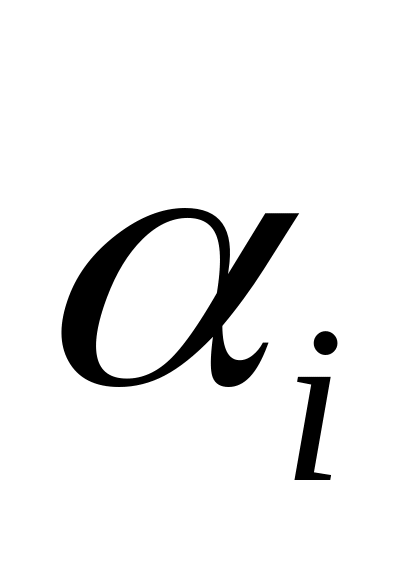
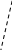
Рисунок 8- К доказательству теоремы Жуковского

Определим величину :

. [4]

Подставив выражение [3] в уравнение [2] получим:

.

Поскольку то с учётом выражения [4] получим:

, или .

Что и требовалось доказать: сумма моментов всех сил относительно полюса плана скоростей, повёрнутого на 90, равна нулю.

Последовательность решения задач кинетостатики способом проф. Н.Е.Жуковского:

1. Механизму задаётся возможное перемещение и строится план возможных скоростей, который затем поворачивается в любую сторону на 90 (по или против часовой стрелки).

2. Все заданные силы, включая силы инерции и уравновешивающую силу, переносятся в соответствующие точки приложения на план скоростей (повёрнутый на 90).

3. Составляется уравнение моментов относительно полюса повёрнутого плана скоростей

т.е. рассматриваем план скоростей как некоторый рычаг с шарнирной опорой в

полюсе, который под действием заданных сил находится в равновесии.